|
|
| Line 1: |
Line 1: |
| − | An Abelian group associated with a ring with an involution which is an anti-isomorphism. In particular, it is defined for any group ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w0970201.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w0970202.png" /> is the fundamental group of a space. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w0970203.png" /> is a [[Poincaré complex|Poincaré complex]], then for a [[Bordism|bordism]] class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w0970204.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w0970205.png" /> there is an [[Obstruction|obstruction]] in this group to the existence of a simple homotopy equivalence in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w0970206.png" />. This obstruction is called the [[Wall invariant|Wall invariant]], cf. [[#References|[1]]].
| + | <!-- |
| | + | w0970201.png |
| | + | $#A+1 = 99 n = 3 |
| | + | $#C+1 = 99 : ~/encyclopedia/old_files/data/W097/W.0907020 Wall group |
| | + | Automatically converted into TeX, above some diagnostics. |
| | + | Please remove this comment and the {{TEX|auto}} line below, |
| | + | if TeX found to be correct. |
| | + | --> |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w0970207.png" /> be a ring with an involution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w0970208.png" /> which is an anti-isomorphism, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w0970209.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702010.png" /> is a left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702011.png" />-module, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702012.png" /> is a left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702013.png" />-module relative to the action <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702014.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702015.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702016.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702017.png" />. This module is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702018.png" />. For a finitely-generated projective <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702019.png" />-module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702020.png" /> there is an isomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702021.png" />: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702022.png" />, and one may identify <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702023.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702024.png" /> using this isomorphism.
| + | {{TEX|auto}} |
| | + | {{TEX|done}} |
| | | | |
| − | A quadratic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702025.png" />-form over a ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702026.png" /> with an involution is a pair <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702027.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702028.png" /> is a finitely-generated projective <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702029.png" />-module and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702030.png" /> is a homomorphism such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702031.png" />. A morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702032.png" /> of forms is a homomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702033.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702034.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702035.png" /> is an isomorphism, then the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702036.png" /> is said to be non-degenerate. A Lagrange plane of a non-degenerate form is a direct summand <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702037.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702038.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702039.png" /> is a direct summand such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702040.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702041.png" /> is called a subLagrange plane. Two Lagrange planes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702042.png" /> of a form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702043.png" /> are called complementary if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702044.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702045.png" />.
| + | An Abelian group associated with a ring with an involution which is an anti-isomorphism. In particular, it is defined for any group ring $ \mathbf Z [ \pi _ {1} ( X)] $, |
| | + | where $ \pi _ {1} ( X) $ |
| | + | is the fundamental group of a space. If $ X $ |
| | + | is a [[Poincaré complex|Poincaré complex]], then for a [[Bordism|bordism]] class $ \alpha $ |
| | + | in $ \Omega _ {*} ( x, \nu ) $ |
| | + | there is an [[Obstruction|obstruction]] in this group to the existence of a simple homotopy equivalence in $ \alpha $. |
| | + | This obstruction is called the [[Wall invariant|Wall invariant]], cf. [[#References|[1]]]. |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702046.png" /> be a projective <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702047.png" />-module. The non-degenerate <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702048.png" />-form | + | Let $ R $ |
| | + | be a ring with an involution $ R \rightarrow R $ |
| | + | which is an anti-isomorphism, i.e. $ \overline{ {ab }}\; = \overline{ {ba }}\; $. |
| | + | If $ P $ |
| | + | is a left $ R $- |
| | + | module, then $ \mathop{\rm Hom} _ {R} ( P, R) $ |
| | + | is a left $ R $- |
| | + | module relative to the action $ ( af ) ( x) = f ( x) \overline{a}\; $, |
| | + | $ f \in \mathop{\rm Hom} _ {R} ( P, R) $, |
| | + | $ a \in R $, |
| | + | $ x \in P $. |
| | + | This module is denoted by $ P ^ {*} $. |
| | + | For a finitely-generated projective $ R $- |
| | + | module $ P $ |
| | + | there is an isomorphism $ P \rightarrow P ^ {**} $: |
| | + | $ x \mapsto ( f \mapsto \overline{ {f ( x) }}\; ) $, |
| | + | and one may identify $ P $ |
| | + | and $ P ^ {**} $ |
| | + | using this isomorphism. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702049.png" /></td> </tr></table>
| + | A quadratic $ (- 1) ^ {k} $- |
| | + | form over a ring $ R $ |
| | + | with an involution is a pair $ ( P, \phi ) $, |
| | + | where $ P $ |
| | + | is a finitely-generated projective $ R $- |
| | + | module and $ \phi : P \rightarrow P ^ {*} $ |
| | + | is a homomorphism such that $ \phi = (- 1) ^ {k} \phi ^ {*} $. |
| | + | A morphism $ f: ( P, \phi ) \rightarrow ( Q, \psi ) $ |
| | + | of forms is a homomorphism $ f: P \rightarrow Q $ |
| | + | such that $ f ^ { * } \psi f = \phi $. |
| | + | If $ \phi $ |
| | + | is an isomorphism, then the form $ ( P, \phi ) $ |
| | + | is said to be non-degenerate. A Lagrange plane of a non-degenerate form is a direct summand $ L \subset P $ |
| | + | for which $ L = \mathop{\rm Ann} \phi ( L) $. |
| | + | If $ L \subset P $ |
| | + | is a direct summand such that $ L \subset \mathop{\rm Ann} \phi ( L) $, |
| | + | then $ L $ |
| | + | is called a subLagrange plane. Two Lagrange planes $ L, G $ |
| | + | of a form $ ( P, \phi ) $ |
| | + | are called complementary if $ L + G = P $ |
| | + | and $ L \cap G = \{ 0 \} $. |
| | | | |
| − | is called Hamiltonian, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702050.png" /> are called its complementary Lagrange planes. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702051.png" /> is a Lagrange plane of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702052.png" />, then the form is isomorphic to the Hamiltonian form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702053.png" />. The choice of a Lagrange plane complementary to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702054.png" /> is equivalent to the choice of an isomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702055.png" />, and this complementary plane can be identified with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702056.png" />.
| + | Let $ L $ |
| | + | be a projective $ R $- |
| | + | module. The non-degenerate $ (- 1) ^ {k} $- |
| | + | form |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702057.png" /> be the Abelian group generated by the equivalence classes (under isomorphism) of non-degenerate quadratic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702058.png" />-forms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702059.png" /> with the relations: 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702060.png" />; and 2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702061.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702062.png" /> has a Lagrange plane. A triple <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702063.png" /> consisting of a non-degenerate <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702064.png" />-form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702065.png" /> and a pair of Lagrange planes is called a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702067.png" />-formation. A formation is said to be trivial if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702069.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702070.png" /> are complementary, and elementary if there exists a Lagrange plane of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702072.png" /> which is complementary to both <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702073.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702074.png" />. The trivial formation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702075.png" /> is called Hamiltonian. By an isomorphism of formations, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702077.png" />, one understands an isomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702078.png" /> of forms for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702079.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702080.png" />. Every trivial formation is isomorphic to the Hamiltonian one.
| + | $$ |
| | + | H _ {(- 1) ^ {k} } ( L) = \ |
| | + | \left ( L \oplus L ^ {*} , \left ( |
| | | | |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702081.png" /> be the Abelian group generated by the equivalence classes (under isomorphism) of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702082.png" />-formations with the following relations: a) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702083.png" />; b) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702084.png" /> if the formation is elementary or trivial.
| + | is called Hamiltonian, and $ L, L ^ {*} \subset L \oplus L ^ {*} $ |
| | + | are called its complementary Lagrange planes. If $ L $ |
| | + | is a Lagrange plane of the form $ ( P, \phi ) $, |
| | + | then the form is isomorphic to the Hamiltonian form $ H _ {(- 1) ^ {k} } ( L) $. |
| | + | The choice of a Lagrange plane complementary to $ L $ |
| | + | is equivalent to the choice of an isomorphism $ ( P, \phi ) \rightarrow H _ {(- 1) ^ {k} } ( L) $, |
| | + | and this complementary plane can be identified with $ L ^ {*} $. |
| | | | |
| − | The groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702085.png" /> are called the Wall groups of the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702086.png" />.
| + | Let $ U _ {2k} ( R ) $ |
| | + | be the Abelian group generated by the equivalence classes (under isomorphism) of non-degenerate quadratic $ (- 1) ^ {k} $- |
| | + | forms $ ( P, \phi ) $ |
| | + | with the relations: 1) $ [( P, \phi )] + [( Q, \psi )] = [( P \oplus Q, \phi \oplus \psi )] $; |
| | + | and 2) $ [( P, \phi )] = 0 $ |
| | + | if $ P $ |
| | + | has a Lagrange plane. A triple $ ( H; F, L) $ |
| | + | consisting of a non-degenerate $ (- 1) ^ {k} $- |
| | + | form $ H $ |
| | + | and a pair of Lagrange planes is called a $ (- 1) ^ {k} $- |
| | + | formation. A formation is said to be trivial if $ F $ |
| | + | and $ L $ |
| | + | are complementary, and elementary if there exists a Lagrange plane of $ H $ |
| | + | which is complementary to both $ F $ |
| | + | and $ L $. |
| | + | The trivial formation $ ( H _ {(- 1) ^ {k} } ( G); G, G) $ |
| | + | is called Hamiltonian. By an isomorphism of formations, $ f: ( H; F, L) \rightarrow ( H _ {1} ; F _ {1} , L _ {1} ) $, |
| | + | one understands an isomorphism $ f: H \rightarrow H _ {1} $ |
| | + | of forms for which $ f ( F ) = F _ {1} $, |
| | + | $ f ( L) = L _ {1} $. |
| | + | Every trivial formation is isomorphic to the Hamiltonian one. |
| | + | |
| | + | Let $ U _ {2k + 1 } ( R ) $ |
| | + | be the Abelian group generated by the equivalence classes (under isomorphism) of $ (- 1) ^ {k} $- |
| | + | formations with the following relations: a) $ [( H; F, L)] \oplus [( H _ {1} ; F _ {1} , L _ {1} )] = [( H \oplus H _ {1} ; F \oplus F _ {1} , L \oplus L _ {1} )] $; |
| | + | b) $ [( H; F, L)] = 0 $ |
| | + | if the formation is elementary or trivial. |
| | + | |
| | + | The groups $ U _ {n} ( R) $ |
| | + | are called the Wall groups of the ring $ R $. |
| | | | |
| | ====References==== | | ====References==== |
| | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> C.T.C. Wall, "Surgery on compact manifolds" , Acad. Press (1970) {{MR|0431216}} {{ZBL|0219.57024}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.A. Ranicki, "The algebraic theory of surgery I" ''Proc. London Math. Soc.'' , '''40''' : 1 (1980) pp. 87–192 {{MR|0560997}} {{MR|0566491}} {{ZBL|0471.57010}} </TD></TR></table> | | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> C.T.C. Wall, "Surgery on compact manifolds" , Acad. Press (1970) {{MR|0431216}} {{ZBL|0219.57024}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.A. Ranicki, "The algebraic theory of surgery I" ''Proc. London Math. Soc.'' , '''40''' : 1 (1980) pp. 87–192 {{MR|0560997}} {{MR|0566491}} {{ZBL|0471.57010}} </TD></TR></table> |
| − |
| |
| − |
| |
| | | | |
| | ====Comments==== | | ====Comments==== |
| − | In the case of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702087.png" /> and the Wall surgery obstruction invariant, the involution on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702088.png" /> is given by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702089.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702090.png" />, where the group homomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702091.png" /> is given by the first Stiefel–Whitney class of the bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702092.png" /> in the bordism class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702093.png" />. | + | In the case of $ R = \mathbf Z [ \pi _ {1} ( X) ] $ |
| | + | and the Wall surgery obstruction invariant, the involution on $ R $ |
| | + | is given by $ g \mapsto w( g) g ^ {-} 1 $, |
| | + | $ g \in \pi _ {1} ( X) $, |
| | + | where the group homomorphism $ w : \pi _ {1} ( X) \rightarrow \{ 1, - 1 \} $ |
| | + | is given by the first Stiefel–Whitney class of the bundle $ \nu $ |
| | + | in the bordism class $ \Omega _ {*} ( X, \nu ) $. |
| | | | |
| − | The Wall groups <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702094.png" /> are more often called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702096.png" />-groups and denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702097.png" />; their theory is referred to as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w09702099.png" />-theory, which is much related to [[K-theory|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w097020100.png" />-theory]]. (Indeed, some authors speak of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w097020101.png" />-theory of forms, [[#References|[a2]]].) The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w097020102.png" />-groups are four-periodic, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w097020103.png" />. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w097020104.png" />-groups can be defined in more general situations and there are a number of somewhat different varieties of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w097020105.png" />-groups, cf. e.g. [[#References|[a1]]], [[#References|[a2]]]. | + | The Wall groups $ U _ {n} ( R) $ |
| | + | are more often called $ L $- |
| | + | groups and denoted by $ L _ {n} ( R) $; |
| | + | their theory is referred to as $ L $- |
| | + | theory, which is much related to [[K-theory| $ K $- |
| | + | theory]]. (Indeed, some authors speak of the $ K $- |
| | + | theory of forms, [[#References|[a2]]].) The $ L $- |
| | + | groups are four-periodic, i.e. $ L _ {n} ( R) \simeq L _ {n+} 4 ( R) $. |
| | + | $ L $- |
| | + | groups can be defined in more general situations and there are a number of somewhat different varieties of $ L $- |
| | + | groups, cf. e.g. [[#References|[a1]]], [[#References|[a2]]]. |
| | | | |
| | ====References==== | | ====References==== |
| | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Ranicki, "Lower <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w097020106.png" />- and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w097020107.png" />-theory" , Cambridge Univ. Press (1992) {{MR|1208729}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Bak, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w097020108.png" />-theory of forms" , Princeton Univ. Press (1981) {{MR|0632404}} {{ZBL|0465.10013}} </TD></TR></table> | | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Ranicki, "Lower <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w097020106.png" />- and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w097020107.png" />-theory" , Cambridge Univ. Press (1992) {{MR|1208729}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Bak, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097020/w097020108.png" />-theory of forms" , Princeton Univ. Press (1981) {{MR|0632404}} {{ZBL|0465.10013}} </TD></TR></table> |
An Abelian group associated with a ring with an involution which is an anti-isomorphism. In particular, it is defined for any group ring $ \mathbf Z [ \pi _ {1} ( X)] $,
where $ \pi _ {1} ( X) $
is the fundamental group of a space. If $ X $
is a Poincaré complex, then for a bordism class $ \alpha $
in $ \Omega _ {*} ( x, \nu ) $
there is an obstruction in this group to the existence of a simple homotopy equivalence in $ \alpha $.
This obstruction is called the Wall invariant, cf. [1].
Let $ R $
be a ring with an involution $ R \rightarrow R $
which is an anti-isomorphism, i.e. $ \overline{ {ab }}\; = \overline{ {ba }}\; $.
If $ P $
is a left $ R $-
module, then $ \mathop{\rm Hom} _ {R} ( P, R) $
is a left $ R $-
module relative to the action $ ( af ) ( x) = f ( x) \overline{a}\; $,
$ f \in \mathop{\rm Hom} _ {R} ( P, R) $,
$ a \in R $,
$ x \in P $.
This module is denoted by $ P ^ {*} $.
For a finitely-generated projective $ R $-
module $ P $
there is an isomorphism $ P \rightarrow P ^ {**} $:
$ x \mapsto ( f \mapsto \overline{ {f ( x) }}\; ) $,
and one may identify $ P $
and $ P ^ {**} $
using this isomorphism.
A quadratic $ (- 1) ^ {k} $-
form over a ring $ R $
with an involution is a pair $ ( P, \phi ) $,
where $ P $
is a finitely-generated projective $ R $-
module and $ \phi : P \rightarrow P ^ {*} $
is a homomorphism such that $ \phi = (- 1) ^ {k} \phi ^ {*} $.
A morphism $ f: ( P, \phi ) \rightarrow ( Q, \psi ) $
of forms is a homomorphism $ f: P \rightarrow Q $
such that $ f ^ { * } \psi f = \phi $.
If $ \phi $
is an isomorphism, then the form $ ( P, \phi ) $
is said to be non-degenerate. A Lagrange plane of a non-degenerate form is a direct summand $ L \subset P $
for which $ L = \mathop{\rm Ann} \phi ( L) $.
If $ L \subset P $
is a direct summand such that $ L \subset \mathop{\rm Ann} \phi ( L) $,
then $ L $
is called a subLagrange plane. Two Lagrange planes $ L, G $
of a form $ ( P, \phi ) $
are called complementary if $ L + G = P $
and $ L \cap G = \{ 0 \} $.
Let $ L $
be a projective $ R $-
module. The non-degenerate $ (- 1) ^ {k} $-
form
$$
H _ {(- 1) ^ {k} } ( L) = \
\left ( L \oplus L ^ {*} , \left (
is called Hamiltonian, and $ L, L ^ {*} \subset L \oplus L ^ {*} $
are called its complementary Lagrange planes. If $ L $
is a Lagrange plane of the form $ ( P, \phi ) $,
then the form is isomorphic to the Hamiltonian form $ H _ {(- 1) ^ {k} } ( L) $.
The choice of a Lagrange plane complementary to $ L $
is equivalent to the choice of an isomorphism $ ( P, \phi ) \rightarrow H _ {(- 1) ^ {k} } ( L) $,
and this complementary plane can be identified with $ L ^ {*} $.
Let $ U _ {2k} ( R ) $
be the Abelian group generated by the equivalence classes (under isomorphism) of non-degenerate quadratic $ (- 1) ^ {k} $-
forms $ ( P, \phi ) $
with the relations: 1) $ [( P, \phi )] + [( Q, \psi )] = [( P \oplus Q, \phi \oplus \psi )] $;
and 2) $ [( P, \phi )] = 0 $
if $ P $
has a Lagrange plane. A triple $ ( H; F, L) $
consisting of a non-degenerate $ (- 1) ^ {k} $-
form $ H $
and a pair of Lagrange planes is called a $ (- 1) ^ {k} $-
formation. A formation is said to be trivial if $ F $
and $ L $
are complementary, and elementary if there exists a Lagrange plane of $ H $
which is complementary to both $ F $
and $ L $.
The trivial formation $ ( H _ {(- 1) ^ {k} } ( G); G, G) $
is called Hamiltonian. By an isomorphism of formations, $ f: ( H; F, L) \rightarrow ( H _ {1} ; F _ {1} , L _ {1} ) $,
one understands an isomorphism $ f: H \rightarrow H _ {1} $
of forms for which $ f ( F ) = F _ {1} $,
$ f ( L) = L _ {1} $.
Every trivial formation is isomorphic to the Hamiltonian one.
Let $ U _ {2k + 1 } ( R ) $
be the Abelian group generated by the equivalence classes (under isomorphism) of $ (- 1) ^ {k} $-
formations with the following relations: a) $ [( H; F, L)] \oplus [( H _ {1} ; F _ {1} , L _ {1} )] = [( H \oplus H _ {1} ; F \oplus F _ {1} , L \oplus L _ {1} )] $;
b) $ [( H; F, L)] = 0 $
if the formation is elementary or trivial.
The groups $ U _ {n} ( R) $
are called the Wall groups of the ring $ R $.
References
In the case of $ R = \mathbf Z [ \pi _ {1} ( X) ] $
and the Wall surgery obstruction invariant, the involution on $ R $
is given by $ g \mapsto w( g) g ^ {-} 1 $,
$ g \in \pi _ {1} ( X) $,
where the group homomorphism $ w : \pi _ {1} ( X) \rightarrow \{ 1, - 1 \} $
is given by the first Stiefel–Whitney class of the bundle $ \nu $
in the bordism class $ \Omega _ {*} ( X, \nu ) $.
The Wall groups $ U _ {n} ( R) $
are more often called $ L $-
groups and denoted by $ L _ {n} ( R) $;
their theory is referred to as $ L $-
theory, which is much related to $ K $-
theory. (Indeed, some authors speak of the $ K $-
theory of forms, [a2].) The $ L $-
groups are four-periodic, i.e. $ L _ {n} ( R) \simeq L _ {n+} 4 ( R) $.
$ L $-
groups can be defined in more general situations and there are a number of somewhat different varieties of $ L $-
groups, cf. e.g. [a1], [a2].
References
| [a1] | A. Ranicki, "Lower 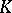 - and - and  -theory" , Cambridge Univ. Press (1992) MR1208729 -theory" , Cambridge Univ. Press (1992) MR1208729 |
| [a2] | A. Bak, "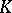 -theory of forms" , Princeton Univ. Press (1981) MR0632404 Zbl 0465.10013 -theory of forms" , Princeton Univ. Press (1981) MR0632404 Zbl 0465.10013 |
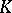 - and
- and  -theory" , Cambridge Univ. Press (1992) MR1208729
-theory" , Cambridge Univ. Press (1992) MR1208729 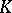 -theory of forms" , Princeton Univ. Press (1981) MR0632404 Zbl 0465.10013
-theory of forms" , Princeton Univ. Press (1981) MR0632404 Zbl 0465.10013