|
|
| Line 1: |
Line 1: |
| − | ''<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t0935602.png" />''
| + | <!-- |
| | + | t0935602.png |
| | + | $#A+1 = 55 n = 1 |
| | + | $#C+1 = 55 : ~/encyclopedia/old_files/data/T093/T.0903560 Trace on a \BMI C sup \ast\EMI\AAhalgebra |
| | + | Automatically converted into TeX, above some diagnostics. |
| | + | Please remove this comment and the {{TEX|auto}} line below, |
| | + | if TeX found to be correct. |
| | + | --> |
| | | | |
| − | An additive functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t0935603.png" /> on the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t0935604.png" /> of positive elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t0935605.png" /> that takes values in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t0935606.png" />, is homogeneous with respect to multiplication by positive numbers and satisfies the condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t0935607.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t0935608.png" />. A trace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t0935609.png" /> is said to be finite if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356011.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356012.png" />, and semi-finite if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356014.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356015.png" />. The finite traces on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356016.png" /> are the restrictions to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356017.png" /> of those positive linear functionals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356018.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356019.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356020.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356021.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356022.png" /> be a trace on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356023.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356024.png" /> be the set of elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356025.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356026.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356027.png" /> be the set of linear combinations of products of pairs of elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356028.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356029.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356030.png" /> are self-adjoint two-sided ideals of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356031.png" />, and there is a unique linear functional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356032.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356033.png" /> that coincides with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356034.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356035.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356036.png" /> be a lower semi-continuous semi-finite trace on a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356037.png" />-algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356038.png" />. Then the formula <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356039.png" /> defines a Hermitian form on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356040.png" />, with respect to which the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356041.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356042.png" /> into itself is continuous for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356043.png" />. Put <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356044.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356045.png" /> be the completion of the quotient space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356046.png" /> with respect to the scalar product defined by the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356047.png" />. By passing to the quotient space and subsequent completion, the operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356048.png" /> determine certain operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356049.png" /> on the Hilbert space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356050.png" />, and the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356051.png" /> is a representation of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356052.png" />-algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356053.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356054.png" />. The mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356055.png" /> establishes a one-to-one correspondence between the set of lower semi-continuous semi-finite traces on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356056.png" /> and the set of representations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356057.png" /> with a trace, defined up to quasi-equivalence. | + | {{TEX|auto}} |
| | + | {{TEX|done}} |
| | + | |
| | + | '' $ A $'' |
| | + | |
| | + | An additive functional $ f $ |
| | + | on the set $ A ^ {+} $ |
| | + | of positive elements of $ A $ |
| | + | that takes values in $ [ 0, + \infty ] $, |
| | + | is homogeneous with respect to multiplication by positive numbers and satisfies the condition $ f ( xx ^ {*} ) = f ( x ^ {*} x) $ |
| | + | for all $ x \in A $. |
| | + | A trace $ f $ |
| | + | is said to be finite if $ f ( x) < + \infty $ |
| | + | for all $ x \in A ^ {+} $, |
| | + | and semi-finite if $ f ( x) = \sup \{ {f ( y) } : {y \in A, y \leq x, f( y) < + \infty } \} $ |
| | + | for all $ x \in A ^ {+} $. |
| | + | The finite traces on $ A $ |
| | + | are the restrictions to $ A ^ {+} $ |
| | + | of those positive linear functionals $ \phi $ |
| | + | on $ A $ |
| | + | such that $ \phi ( xy) = \phi ( yx) $ |
| | + | for all $ x, y \in A $. |
| | + | Let $ f $ |
| | + | be a trace on $ A $, |
| | + | let $ \mathfrak N _ {f} $ |
| | + | be the set of elements $ x \in A $ |
| | + | such that $ f ( xx ^ {*} ) < + \infty $, |
| | + | and let $ \mathfrak M _ {f} $ |
| | + | be the set of linear combinations of products of pairs of elements of $ \mathfrak N _ {f} $. |
| | + | Then $ \mathfrak N _ {f} $ |
| | + | and $ \mathfrak M _ {f} $ |
| | + | are self-adjoint two-sided ideals of $ A $, |
| | + | and there is a unique linear functional $ \phi $ |
| | + | on $ \mathfrak M _ {f} $ |
| | + | that coincides with $ f $ |
| | + | on $ \mathfrak M _ {f} \cap A ^ {+} $. |
| | + | Let $ f $ |
| | + | be a lower semi-continuous semi-finite trace on a $ C ^ {*} $- |
| | + | algebra $ A $. |
| | + | Then the formula $ s ( x, y) = \phi ( y ^ {*} x) $ |
| | + | defines a Hermitian form on $ \mathfrak N _ {f} $, |
| | + | with respect to which the mapping $ \lambda _ {f} ( x): x \mapsto xy $ |
| | + | of $ \mathfrak N _ {f} $ |
| | + | into itself is continuous for any $ x \in A $. |
| | + | Put $ N _ {f} = \{ {x \in \mathfrak N _ {f} } : {s ( x, x) = 0 } \} $, |
| | + | and let $ H _ {f} $ |
| | + | be the completion of the quotient space $ \mathfrak N _ {f} /N _ {f} $ |
| | + | with respect to the scalar product defined by the form $ s $. |
| | + | By passing to the quotient space and subsequent completion, the operators $ \lambda _ {f} ( x) $ |
| | + | determine certain operators $ \pi _ {f} ( x) $ |
| | + | on the Hilbert space $ H _ {f} $, |
| | + | and the mapping $ x \mapsto \pi _ {f} ( x) $ |
| | + | is a representation of the $ C ^ {*} $- |
| | + | algebra $ A $ |
| | + | in $ H _ {f} $. |
| | + | The mapping $ f \mapsto \pi _ {f} $ |
| | + | establishes a one-to-one correspondence between the set of lower semi-continuous semi-finite traces on $ A $ |
| | + | and the set of representations of $ A $ |
| | + | with a trace, defined up to quasi-equivalence. |
| | | | |
| | ====References==== | | ====References==== |
| | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J. Dixmier, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356058.png" /> algebras" , North-Holland (1977) (Translated from French)</TD></TR></table> | | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J. Dixmier, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356058.png" /> algebras" , North-Holland (1977) (Translated from French)</TD></TR></table> |
| − |
| |
| − |
| |
| | | | |
| | ====Comments==== | | ====Comments==== |
| − | Cf. also [[C*-algebra|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093560/t09356059.png" />-algebra]]; [[Trace|Trace]]; [[Quasi-equivalent representations|Quasi-equivalent representations]]. | + | Cf. also [[C*-algebra| $ C ^ {*} $- |
| | + | algebra]]; [[Trace|Trace]]; [[Quasi-equivalent representations|Quasi-equivalent representations]]. |
| | | | |
| | ====References==== | | ====References==== |
| | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> O. Bratteli, D.W. Robinson, "Operator algebras and quantum statistical mechanics" , '''1''' , Springer (1979)</TD></TR></table> | | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> O. Bratteli, D.W. Robinson, "Operator algebras and quantum statistical mechanics" , '''1''' , Springer (1979)</TD></TR></table> |
$ A $
An additive functional $ f $
on the set $ A ^ {+} $
of positive elements of $ A $
that takes values in $ [ 0, + \infty ] $,
is homogeneous with respect to multiplication by positive numbers and satisfies the condition $ f ( xx ^ {*} ) = f ( x ^ {*} x) $
for all $ x \in A $.
A trace $ f $
is said to be finite if $ f ( x) < + \infty $
for all $ x \in A ^ {+} $,
and semi-finite if $ f ( x) = \sup \{ {f ( y) } : {y \in A, y \leq x, f( y) < + \infty } \} $
for all $ x \in A ^ {+} $.
The finite traces on $ A $
are the restrictions to $ A ^ {+} $
of those positive linear functionals $ \phi $
on $ A $
such that $ \phi ( xy) = \phi ( yx) $
for all $ x, y \in A $.
Let $ f $
be a trace on $ A $,
let $ \mathfrak N _ {f} $
be the set of elements $ x \in A $
such that $ f ( xx ^ {*} ) < + \infty $,
and let $ \mathfrak M _ {f} $
be the set of linear combinations of products of pairs of elements of $ \mathfrak N _ {f} $.
Then $ \mathfrak N _ {f} $
and $ \mathfrak M _ {f} $
are self-adjoint two-sided ideals of $ A $,
and there is a unique linear functional $ \phi $
on $ \mathfrak M _ {f} $
that coincides with $ f $
on $ \mathfrak M _ {f} \cap A ^ {+} $.
Let $ f $
be a lower semi-continuous semi-finite trace on a $ C ^ {*} $-
algebra $ A $.
Then the formula $ s ( x, y) = \phi ( y ^ {*} x) $
defines a Hermitian form on $ \mathfrak N _ {f} $,
with respect to which the mapping $ \lambda _ {f} ( x): x \mapsto xy $
of $ \mathfrak N _ {f} $
into itself is continuous for any $ x \in A $.
Put $ N _ {f} = \{ {x \in \mathfrak N _ {f} } : {s ( x, x) = 0 } \} $,
and let $ H _ {f} $
be the completion of the quotient space $ \mathfrak N _ {f} /N _ {f} $
with respect to the scalar product defined by the form $ s $.
By passing to the quotient space and subsequent completion, the operators $ \lambda _ {f} ( x) $
determine certain operators $ \pi _ {f} ( x) $
on the Hilbert space $ H _ {f} $,
and the mapping $ x \mapsto \pi _ {f} ( x) $
is a representation of the $ C ^ {*} $-
algebra $ A $
in $ H _ {f} $.
The mapping $ f \mapsto \pi _ {f} $
establishes a one-to-one correspondence between the set of lower semi-continuous semi-finite traces on $ A $
and the set of representations of $ A $
with a trace, defined up to quasi-equivalence.
References
| [1] | J. Dixmier, "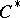 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
Cf. also $ C ^ {*} $-
algebra; Trace; Quasi-equivalent representations.
References
| [a1] | O. Bratteli, D.W. Robinson, "Operator algebras and quantum statistical mechanics" , 1 , Springer (1979) |
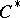 algebras" , North-Holland (1977) (Translated from French)
algebras" , North-Holland (1977) (Translated from French)