Difference between revisions of "Syracuse problem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | s1103302.png | ||
| + | $#A+1 = 33 n = 3 | ||
| + | $#C+1 = 33 : ~/encyclopedia/old_files/data/S110/S.1100330 Syracuse problem, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | This problem concerns the iteration of the Collatz mapping that sends a positive integer | + | {{TEX|auto}} |
| + | {{TEX|done}} | ||
| + | |||
| + | '' $ ( 3x + 1 ) $- | ||
| + | problem, Collatz problem, Hasse algorithm, Hasse–Collatz problem, Kakutani problem, Ulam problem'' | ||
| + | |||
| + | This problem concerns the iteration of the Collatz mapping that sends a positive integer $ a _ {n} $ | ||
| + | to $ a _ {n + 1 } = { {a _ {n} } / 2 } $( | ||
| + | $ a _ {n} $ | ||
| + | even) or to $ 3a _ {n + 1 } + 1 $( | ||
| + | $ a _ {n} $ | ||
| + | odd). The $ ( 3x + 1 ) $- | ||
| + | conjecture (also called the Collatz conjecture) asserts that for any starting value $ a _ {0} \geq 2 $ | ||
| + | there is some iterate $ a _ {n} = 1 $. | ||
Some examples are: | Some examples are: | ||
| − | a) | + | a) $ 1 \rightarrow 4 \rightarrow 2 \rightarrow 1 $; |
| − | b) | + | b) $ 5 \rightarrow 16 \rightarrow 8 \rightarrow 4 \rightarrow 2 \rightarrow 1 $; |
| − | c) | + | c) $ 7 \rightarrow 22 \rightarrow 11 \rightarrow 34 \rightarrow 17 \rightarrow 52 \rightarrow 26 \rightarrow 13 \rightarrow 40 \rightarrow 20 \rightarrow 10 \rightarrow 5 \rightarrow 16 \rightarrow 8 \rightarrow 4 \rightarrow 2 \rightarrow 1 $. |
| − | If | + | If $ a _ {0} $ |
| + | is allowed to be a negative integer, the conjecture is not true, as is shown by the example $ - 5 \rightarrow - 14 \rightarrow - 7 \rightarrow - 20 \rightarrow - 10 \rightarrow - 5 $. | ||
| + | In other words: the Collatz conjecture with $ 3 a _ {n} + 1 $ | ||
| + | replaced by $ 3 a _ {n} - 1 $ | ||
| + | does not hold. | ||
| − | This conjecture is generally attributed to L. Collatz, who studied similar problems in the 1930s. It has been numerically verified for all < | + | This conjecture is generally attributed to L. Collatz, who studied similar problems in the 1930s. It has been numerically verified for all $ a _ {0} < 6 \times 10 ^ {13 } $[[#References|[a5]]]. The conjecture is unsolved (1996) and apparently extremely difficult despite its simple appearance. General references and surveys on the problem are [[#References|[a3]]], [[#References|[a4]]], [[#References|[a6]]]. |
| − | There is no periodic orbit of the Collatz mapping of period less than | + | There is no periodic orbit of the Collatz mapping of period less than $ 17087915 $, |
| + | except the orbit $ \{ 1,4,2 \} $. | ||
| + | The set of positive integers $ a _ {0} $ | ||
| + | that have some iterate $ a _ {n} $ | ||
| + | less than $ a _ {0} $ | ||
| + | has density one. At least $ x ^ {8/10 } $ | ||
| + | of all positive integers $ a _ {0} $ | ||
| + | less than $ x $ | ||
| + | have some iterate $ a _ {n} = 1 $, | ||
| + | [[#References|[a1]]]. | ||
| − | J.H. Conway [[#References|[a2]]] showed that a certain generalization of the | + | J.H. Conway [[#References|[a2]]] showed that a certain generalization of the $ ( 3x + 1 ) $- |
| + | problem is non-computable. He defined a particular mapping $ f $ | ||
| + | from the positive integers into the positive integers of the form $ f ( n ) = b _ {n} n $, | ||
| + | in which $ \{ b _ {n} \} $ | ||
| + | is periodic (modulo some $ N _ {0} $) | ||
| + | for a fixed modulus $ N _ {0} $, | ||
| + | which has the property that the set | ||
| − | + | $$ | |
| + | \left \{ m : {\textrm{ some iterate } f ^ {( k ) } ( m ) = 2 ^ {j} , \textrm{ some } j \geq 0 } \right \} | ||
| + | $$ | ||
is recursively enumerable but not recursive. | is recursively enumerable but not recursive. | ||
Latest revision as of 08:24, 6 June 2020
$ ( 3x + 1 ) $-
problem, Collatz problem, Hasse algorithm, Hasse–Collatz problem, Kakutani problem, Ulam problem
This problem concerns the iteration of the Collatz mapping that sends a positive integer $ a _ {n} $ to $ a _ {n + 1 } = { {a _ {n} } / 2 } $( $ a _ {n} $ even) or to $ 3a _ {n + 1 } + 1 $( $ a _ {n} $ odd). The $ ( 3x + 1 ) $- conjecture (also called the Collatz conjecture) asserts that for any starting value $ a _ {0} \geq 2 $ there is some iterate $ a _ {n} = 1 $.
Some examples are:
a) $ 1 \rightarrow 4 \rightarrow 2 \rightarrow 1 $;
b) $ 5 \rightarrow 16 \rightarrow 8 \rightarrow 4 \rightarrow 2 \rightarrow 1 $;
c) $ 7 \rightarrow 22 \rightarrow 11 \rightarrow 34 \rightarrow 17 \rightarrow 52 \rightarrow 26 \rightarrow 13 \rightarrow 40 \rightarrow 20 \rightarrow 10 \rightarrow 5 \rightarrow 16 \rightarrow 8 \rightarrow 4 \rightarrow 2 \rightarrow 1 $.
If $ a _ {0} $ is allowed to be a negative integer, the conjecture is not true, as is shown by the example $ - 5 \rightarrow - 14 \rightarrow - 7 \rightarrow - 20 \rightarrow - 10 \rightarrow - 5 $. In other words: the Collatz conjecture with $ 3 a _ {n} + 1 $ replaced by $ 3 a _ {n} - 1 $ does not hold.
This conjecture is generally attributed to L. Collatz, who studied similar problems in the 1930s. It has been numerically verified for all $ a _ {0} < 6 \times 10 ^ {13 } $[a5]. The conjecture is unsolved (1996) and apparently extremely difficult despite its simple appearance. General references and surveys on the problem are [a3], [a4], [a6].
There is no periodic orbit of the Collatz mapping of period less than $ 17087915 $, except the orbit $ \{ 1,4,2 \} $. The set of positive integers $ a _ {0} $ that have some iterate $ a _ {n} $ less than $ a _ {0} $ has density one. At least $ x ^ {8/10 } $ of all positive integers $ a _ {0} $ less than $ x $ have some iterate $ a _ {n} = 1 $, [a1].
J.H. Conway [a2] showed that a certain generalization of the $ ( 3x + 1 ) $- problem is non-computable. He defined a particular mapping $ f $ from the positive integers into the positive integers of the form $ f ( n ) = b _ {n} n $, in which $ \{ b _ {n} \} $ is periodic (modulo some $ N _ {0} $) for a fixed modulus $ N _ {0} $, which has the property that the set
$$ \left \{ m : {\textrm{ some iterate } f ^ {( k ) } ( m ) = 2 ^ {j} , \textrm{ some } j \geq 0 } \right \} $$
is recursively enumerable but not recursive.
References
| [a1] | D. Applegate, J.C. Lagarias, "Density bounds for the 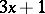 problem II. Krasikov inequalities" Math. Comp. , 64 (1995) pp. 427–438 problem II. Krasikov inequalities" Math. Comp. , 64 (1995) pp. 427–438 |
| [a2] | J.H. Conway, "Unpredictable Iterations" , Proc. 1972 Number Theory Conf. Univ. Colorado, Boulder (1972) pp. 49–52 |
| [a3] | R.K. Guy, "Unsolved problems in number theory" , Springer (1994) pp. Problem E16 (Edition: Second) |
| [a4] | J.C. Lagarias, "The 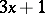 problem and its generalizations" Amer. Math. Monthly , 92 (1985) pp. 3–23 problem and its generalizations" Amer. Math. Monthly , 92 (1985) pp. 3–23 |
| [a5] | G. Leavens, M. Vermeulen, "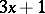 search programs" Computers & Mathematics, with Applications , 24 : 11 (1992) pp. 79–99 search programs" Computers & Mathematics, with Applications , 24 : 11 (1992) pp. 79–99 |
| [a6] | H.A. Müller, "Das "3n+1" Problem" Mitteil. Math. Ges. Hamburg , 12 (1991) pp. 231–251 |
Syracuse problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Syracuse_problem&oldid=48940