Difference between revisions of "Subordination principle"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | One of the forms of the [[Lindelöf principle|Lindelöf principle]], which employs the concept of subordination of functions. Let | + | <!-- |
| + | s0909901.png | ||
| + | $#A+1 = 68 n = 1 | ||
| + | $#C+1 = 68 : ~/encyclopedia/old_files/data/S090/S.0900990 Subordination principle | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | One of the forms of the [[Lindelöf principle|Lindelöf principle]], which employs the concept of subordination of functions. Let $ \omega ( x) $ | ||
| + | be any function regular in the disc $ | z | < 1 $ | ||
| + | and satisfying the conditions $ \omega ( 0) = 0 $, | ||
| + | $ | \omega ( z) | < 1 $ | ||
| + | in $ | z | < 1 $; | ||
| + | let $ F( z) $ | ||
| + | be a meromorphic function in $ | z | < 1 $. | ||
| + | If the function $ f( z) $ | ||
| + | has the form $ f( z) = F( \omega ( z)) $, | ||
| + | then $ f( z) $ | ||
| + | is called subordinate to the function $ F( z) $ | ||
| + | in the disc $ | z | < 1 $, | ||
| + | while $ F( z) $ | ||
| + | is called the subordinating function. This subordination relation is denoted by $ f( z) \prec F( z) $. | ||
| + | In the simplest case where $ F( z) $ | ||
| + | is a [[Univalent function|univalent function]] in $ | z | < 1 $, | ||
| + | this relation simply means that $ f( 0) = F( 0) $ | ||
| + | and that $ f( z) $ | ||
| + | does not take any values in the disc $ | z | < 1 $ | ||
| + | that are not taken there by $ F( z) $. | ||
| + | The following basic theorems apply. | ||
===Theorem 1.=== | ===Theorem 1.=== | ||
| − | Let the function | + | Let the function $ w = F( z) $ |
| + | be meromorphic in the disc $ | z | < 1 $ | ||
| + | and map it on the [[Riemann surface|Riemann surface]] $ G( F ) $. | ||
| + | Let $ G _ {r} ( F ) $ | ||
| + | be the part of $ G( F ) $ | ||
| + | corresponding to $ | z | \leq r $, | ||
| + | $ r < 1 $. | ||
| + | If $ f( z) \prec F( z) $, | ||
| + | then the values of $ f( z) $ | ||
| + | in $ | z | \leq r $( | ||
| + | under [[Analytic continuation|analytic continuation]] from $ f( 0) = F( 0) $) | ||
| + | lie in $ G _ {r} ( F ) $, | ||
| + | and the boundary points in $ G _ {r} ( F ) $ | ||
| + | are obtained only for $ f( z) = F( \epsilon z) $, | ||
| + | $ | \epsilon | = 1 $[[#References|[2]]]. | ||
===Theorem 2.=== | ===Theorem 2.=== | ||
| − | If | + | If $ f( z) \prec F( z) $ |
| + | and if $ F( z) $ | ||
| + | is regular in $ | z | \leq r $, | ||
| + | $ r < 1 $, | ||
| + | then setting | ||
| − | + | $$ | |
| + | M _ \lambda ( r, f ) = \ | ||
| + | \left \{ | ||
| + | \frac{1}{2 \pi } | ||
| + | \int\limits _ { 0 } ^ { {2 } \pi } | | ||
| + | f( re ^ {i \theta } ) | ^ \lambda d \phi \right \} ^ {1/ \lambda } ,\ \ | ||
| + | \lambda \geq 0 , | ||
| + | $$ | ||
| − | one has | + | one has $ M _ \lambda ( r, f ) \leq M _ \lambda ( r, F ) $, |
| + | $ \lambda \geq 0 $, | ||
| + | $ 0 \leq r < 1 $, | ||
| + | [[#References|[1]]]. | ||
===Theorem 3.=== | ===Theorem 3.=== | ||
| − | If | + | If $ f( z) \prec F( z) $ |
| + | and $ F( z) $ | ||
| + | is regular at $ z = 0 $, | ||
| + | then for the coefficients of the expansions $ f( z) = \sum _ {n=} 0 ^ \infty a _ {n} z ^ {n} $, | ||
| + | $ F( z) = \sum _ {n=} 0 ^ \infty A _ {n} z ^ {n} $ | ||
| + | one has $ \sum _ {n=} 1 ^ {m} | a _ {n} | ^ {2} \leq \sum _ {n=} 1 ^ {m} | A _ {n} | ^ {2} $, | ||
| + | $ m = 1, 2 \dots $[[#References|[2]]]. | ||
| − | The general theory of subordination is useful in considering the set of values taken or produced by an analytic function. The subordination relation can be used in two different ways. First, one can start from a given function | + | The general theory of subordination is useful in considering the set of values taken or produced by an analytic function. The subordination relation can be used in two different ways. First, one can start from a given function $ F( z) $ |
| + | and examine the behaviour of all $ f( z) $ | ||
| + | subordinate to $ F( z) $. | ||
| + | If $ F( z) $ | ||
| + | is completely known, then the region $ G _ {r} ( F ) $ | ||
| + | in which the values of $ f( z) $ | ||
| + | lie is also known (Theorem 1) as well as an upper bound on the integral means $ M _ \gamma ( r, f ) $( | ||
| + | Theorem 2). If also $ F( z) $ | ||
| + | is regular at $ z = 0 $, | ||
| + | there are upper bounds for the coefficients of $ f( z) $( | ||
| + | Theorem 3). Secondly, one can consider a function $ f( z) $ | ||
| + | that is meromorphic in the disc $ | z | < 1 $ | ||
| + | and whose properties imply that it cannot be subordinate to a given function $ F( z) $ | ||
| + | in $ | z | < 1 $. | ||
| + | If here $ F( z) $, | ||
| + | for example, is univalent, then $ f( z) $ | ||
| + | necessarily takes values outside $ G( F ) $ | ||
| + | in $ | z | < 1 $. | ||
| + | These ideas of using the subordination relation illustrate the subordination principle and can be extended to multiply-connected domains [[#References|[3]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> J.E. Littlewood, "On inequalities in the theory of functions" ''Proc. Lond. Math. Soc. (2)'' , '''23''' (1925) pp. 481–519</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> W. Rogosinski, "On subordinate functions" ''Proc. Cambridge Philos. Soc.'' , '''35''' (1939) pp. 1–26</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> Yu. Alenitsyn, "A generalization of the subordination principle to multiply-connected domains" ''Trudy Mat. Inst. Steklov.'' , '''60''' (1961) pp. 5–21 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> W. Rogosinski, ''Schr. K. Gelehrt. Gesellsch. Naturwiss. Kl.'' , '''8''' : 1 (1931) pp. 1–31</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> W. Rogosinski, "On a theorem of Bieberbach–Eilenberg" ''J. Lond. Math. Soc.'' , '''14''' : 53 (1939) pp. 4–11</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> W. Rogosinski, "On the coefficients of subordinate functions" ''Proc. London Math. Soc.'' , '''48''' (1943) pp. 48–82</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> J.E. Littlewood, "Lectures on the theory of functions" , Oxford Univ. Press (1944)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> G.M. Goluzin, "Geometric theory of functions of a complex variable" , ''Transl. Math. Monogr.'' , '''26''' , Amer. Math. Soc. (1969) (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J.E. Littlewood, "On inequalities in the theory of functions" ''Proc. Lond. Math. Soc. (2)'' , '''23''' (1925) pp. 481–519</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> W. Rogosinski, "On subordinate functions" ''Proc. Cambridge Philos. Soc.'' , '''35''' (1939) pp. 1–26</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> Yu. Alenitsyn, "A generalization of the subordination principle to multiply-connected domains" ''Trudy Mat. Inst. Steklov.'' , '''60''' (1961) pp. 5–21 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> W. Rogosinski, ''Schr. K. Gelehrt. Gesellsch. Naturwiss. Kl.'' , '''8''' : 1 (1931) pp. 1–31</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> W. Rogosinski, "On a theorem of Bieberbach–Eilenberg" ''J. Lond. Math. Soc.'' , '''14''' : 53 (1939) pp. 4–11</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> W. Rogosinski, "On the coefficients of subordinate functions" ''Proc. London Math. Soc.'' , '''48''' (1943) pp. 48–82</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> J.E. Littlewood, "Lectures on the theory of functions" , Oxford Univ. Press (1944)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> G.M. Goluzin, "Geometric theory of functions of a complex variable" , ''Transl. Math. Monogr.'' , '''26''' , Amer. Math. Soc. (1969) (Translated from Russian)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.L. Duren, "Theory of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090990/s09099069.png" /> spaces" , Acad. Press (1970)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.L. Duren, "Theory of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090990/s09099069.png" /> spaces" , Acad. Press (1970)</TD></TR></table> | ||
Revision as of 08:24, 6 June 2020
One of the forms of the Lindelöf principle, which employs the concept of subordination of functions. Let $ \omega ( x) $
be any function regular in the disc $ | z | < 1 $
and satisfying the conditions $ \omega ( 0) = 0 $,
$ | \omega ( z) | < 1 $
in $ | z | < 1 $;
let $ F( z) $
be a meromorphic function in $ | z | < 1 $.
If the function $ f( z) $
has the form $ f( z) = F( \omega ( z)) $,
then $ f( z) $
is called subordinate to the function $ F( z) $
in the disc $ | z | < 1 $,
while $ F( z) $
is called the subordinating function. This subordination relation is denoted by $ f( z) \prec F( z) $.
In the simplest case where $ F( z) $
is a univalent function in $ | z | < 1 $,
this relation simply means that $ f( 0) = F( 0) $
and that $ f( z) $
does not take any values in the disc $ | z | < 1 $
that are not taken there by $ F( z) $.
The following basic theorems apply.
Theorem 1.
Let the function $ w = F( z) $ be meromorphic in the disc $ | z | < 1 $ and map it on the Riemann surface $ G( F ) $. Let $ G _ {r} ( F ) $ be the part of $ G( F ) $ corresponding to $ | z | \leq r $, $ r < 1 $. If $ f( z) \prec F( z) $, then the values of $ f( z) $ in $ | z | \leq r $( under analytic continuation from $ f( 0) = F( 0) $) lie in $ G _ {r} ( F ) $, and the boundary points in $ G _ {r} ( F ) $ are obtained only for $ f( z) = F( \epsilon z) $, $ | \epsilon | = 1 $[2].
Theorem 2.
If $ f( z) \prec F( z) $ and if $ F( z) $ is regular in $ | z | \leq r $, $ r < 1 $, then setting
$$ M _ \lambda ( r, f ) = \ \left \{ \frac{1}{2 \pi } \int\limits _ { 0 } ^ { {2 } \pi } | f( re ^ {i \theta } ) | ^ \lambda d \phi \right \} ^ {1/ \lambda } ,\ \ \lambda \geq 0 , $$
one has $ M _ \lambda ( r, f ) \leq M _ \lambda ( r, F ) $, $ \lambda \geq 0 $, $ 0 \leq r < 1 $, [1].
Theorem 3.
If $ f( z) \prec F( z) $ and $ F( z) $ is regular at $ z = 0 $, then for the coefficients of the expansions $ f( z) = \sum _ {n=} 0 ^ \infty a _ {n} z ^ {n} $, $ F( z) = \sum _ {n=} 0 ^ \infty A _ {n} z ^ {n} $ one has $ \sum _ {n=} 1 ^ {m} | a _ {n} | ^ {2} \leq \sum _ {n=} 1 ^ {m} | A _ {n} | ^ {2} $, $ m = 1, 2 \dots $[2].
The general theory of subordination is useful in considering the set of values taken or produced by an analytic function. The subordination relation can be used in two different ways. First, one can start from a given function $ F( z) $ and examine the behaviour of all $ f( z) $ subordinate to $ F( z) $. If $ F( z) $ is completely known, then the region $ G _ {r} ( F ) $ in which the values of $ f( z) $ lie is also known (Theorem 1) as well as an upper bound on the integral means $ M _ \gamma ( r, f ) $( Theorem 2). If also $ F( z) $ is regular at $ z = 0 $, there are upper bounds for the coefficients of $ f( z) $( Theorem 3). Secondly, one can consider a function $ f( z) $ that is meromorphic in the disc $ | z | < 1 $ and whose properties imply that it cannot be subordinate to a given function $ F( z) $ in $ | z | < 1 $. If here $ F( z) $, for example, is univalent, then $ f( z) $ necessarily takes values outside $ G( F ) $ in $ | z | < 1 $. These ideas of using the subordination relation illustrate the subordination principle and can be extended to multiply-connected domains [3].
References
| [1] | J.E. Littlewood, "On inequalities in the theory of functions" Proc. Lond. Math. Soc. (2) , 23 (1925) pp. 481–519 |
| [2] | W. Rogosinski, "On subordinate functions" Proc. Cambridge Philos. Soc. , 35 (1939) pp. 1–26 |
| [3] | Yu. Alenitsyn, "A generalization of the subordination principle to multiply-connected domains" Trudy Mat. Inst. Steklov. , 60 (1961) pp. 5–21 (In Russian) |
| [4] | W. Rogosinski, Schr. K. Gelehrt. Gesellsch. Naturwiss. Kl. , 8 : 1 (1931) pp. 1–31 |
| [5] | W. Rogosinski, "On a theorem of Bieberbach–Eilenberg" J. Lond. Math. Soc. , 14 : 53 (1939) pp. 4–11 |
| [6] | W. Rogosinski, "On the coefficients of subordinate functions" Proc. London Math. Soc. , 48 (1943) pp. 48–82 |
| [7] | J.E. Littlewood, "Lectures on the theory of functions" , Oxford Univ. Press (1944) |
| [8] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
Comments
References
| [a1] | P.L. Duren, "Theory of 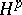 spaces" , Acad. Press (1970) spaces" , Acad. Press (1970) |
Subordination principle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Subordination_principle&oldid=48897