Difference between revisions of "Search algorithm"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | s1100701.png | ||
| + | $#A+1 = 49 n = 0 | ||
| + | $#C+1 = 49 : ~/encyclopedia/old_files/data/S110/S.1100070 Search algorithm | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''on a graph, graph search'' | ''on a graph, graph search'' | ||
| − | An [[Algorithm|algorithm]] that tries to find all nodes in a [[Network|network]] or [[Graph|graph]] that satisfy a given property. Such algorithms are also used, e.g., to optimize a function on a graph or network or on a set which can easily be turned into a graph, such as | + | An [[Algorithm|algorithm]] that tries to find all nodes in a [[Network|network]] or [[Graph|graph]] that satisfy a given property. Such algorithms are also used, e.g., to optimize a function on a graph or network or on a set which can easily be turned into a graph, such as $ \{ 0,1 \} ^ {n} $. |
| + | (Two $ 0 $- | ||
| + | $ 1 $ | ||
| + | vectors of length $ n $ | ||
| + | are joined if an only if they differ in precisely one coordinate, yielding a hypercube.) Thus, these are definite relations and similarities between graph search and search theory as a systematic optimization technique (of enumeration type) [[#References|[a3]]]. See [[#References|[a4]]] for a very complete overview of global optimization (from the search point of view, including random search). | ||
| − | Two of the most often used search techniques in graphs or networks are depth-first search and breadth-first search. Let | + | Two of the most often used search techniques in graphs or networks are depth-first search and breadth-first search. Let $ \Gamma = ( V,E ) $ |
| + | be a finite oriented graph (cf. [[Graph, oriented|Graph, oriented]]). For each $ v \in V $, | ||
| + | let $ A ( v ) $ | ||
| + | be the set of edges (arcs) issuing from $ v $. | ||
| + | For instance, in Fig.a1, $ A ( 1 ) = \{ ( 1,2 ) , ( 1,4 ) \} $, | ||
| + | $ A ( 3 ) = \{ ( 3,6 ) \} $, | ||
| + | $ A ( 7 ) = \emptyset $. | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s110070a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s110070a.gif" /> | ||
| Line 9: | Line 31: | ||
Figure: s110070a | Figure: s110070a | ||
| − | It is assumed that the sets | + | It is assumed that the sets $ A ( v ) $, |
| + | $ v \in V $, | ||
| + | are given some fixed total order (cf. also [[Totally ordered set|Totally ordered set]]) for all $ v $. | ||
| + | The following algorithm picks out all nodes in $ \Gamma $ | ||
| + | that are reachable from a source node $ s $ | ||
| + | by means of a directed path. These nodes will be marked. Central to the algorithm is a certain list $ L $, | ||
| + | which can be seen as a sort of wave front indicating the boundary of the spreading blob of marked points: | ||
unmark all points; | unmark all points; | ||
| − | mark the source node | + | mark the source node $ s $; |
| − | set | + | set $ L = \{ s \} $; |
| − | as long as | + | as long as $ L $ |
| + | is non-empty, run the following iterative procedure: | ||
| − | choose a node | + | choose a node $ i \in L $; |
| − | select the first oriented edge | + | select the first oriented edge $ ( i,j ) \in A ( i ) $ |
| + | that runs (from $ i $) | ||
| + | to an unmarked node $ j $( | ||
| + | if any); | ||
| − | mark the node | + | mark the node $ j $; |
| − | define the function | + | define the function $ { \mathop{\rm revp} } $ |
| + | on $ j $ | ||
| + | as $ { \mathop{\rm revp} } ( j ) = i $; | ||
| − | add | + | add $ j $ |
| + | to $ L $; | ||
| − | if there is no | + | if there is no $ ( i,j ) \in A ( i ) $ |
| + | that runs to an unmarked node $ j $, | ||
| + | remove $ i $ | ||
| + | from $ L $. | ||
| − | stop when | + | stop when $ L $ |
| + | is empty. | ||
| − | The algorithm does not yet specify how to select a node from | + | The algorithm does not yet specify how to select a node from $ L $. |
| + | If $ L $ | ||
| + | is treated as a queue, i.e., the node selected is the one that has been longest in $ L $( | ||
| + | first-in-first-out) the result is breadth-first search. On the other hand, if $ L $ | ||
| + | is treated as a stack, i.e., the node selected is the one that was last added to $ L $( | ||
| + | last-in-first-out) the result is depth-first search. | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s110070b.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s110070b.gif" /> | ||
| Line 41: | Line 85: | ||
For an oriented tree as in Fig.a2 (downwards oriented), starting at the indicated node, breadth-first search will first pick the three children of the node indicated (in some order) and then will proceed to the next layer. Depth-first search will first pick a maximal downward chain (maximal in the sense that it ends at a leaf, not necessarily maximal in length) and then go back to another child of the last branching node in that chain. | For an oriented tree as in Fig.a2 (downwards oriented), starting at the indicated node, breadth-first search will first pick the three children of the node indicated (in some order) and then will proceed to the next layer. Depth-first search will first pick a maximal downward chain (maximal in the sense that it ends at a leaf, not necessarily maximal in length) and then go back to another child of the last branching node in that chain. | ||
| − | The order which is used on the edge sets | + | The order which is used on the edge sets $ A ( v ) $ |
| + | also matters, but not as much. | ||
| − | The edges picked out by the function | + | The edges picked out by the function $ { \mathop{\rm revp} } $( |
| + | reverse path), i.e., the edges $ ( { \mathop{\rm revp} } ( j ) ,j ) $ | ||
| + | form an oriented tree comprising the reachable nodes from the source node $ s $. | ||
| − | The results of the algorithm in four cases are given below for the case of Fig.a1. | + | The results of the algorithm in four cases are given below for the case of Fig.a1.<table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1">search</td> <td colname="2" style="background-color:white;" colspan="1">marking</td> <td colname="3" style="background-color:white;" colspan="1">oriented</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">method</td> <td colname="2" style="background-color:white;" colspan="1">sequence</td> <td colname="3" style="background-color:white;" colspan="1">tree</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> <td colname="2" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">breadth first,</td> <td colname="2" style="background-color:white;" colspan="1">1 2 4 3 5 6 7</td> <td colname="3" style="background-color:white;" colspan="1"> |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">lexicographic</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">order</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">on the | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">lexicographic</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">order</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">on the $ A ( i ) $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> <td colname="2" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">breadth first,</td> <td colname="2" style="background-color:white;" colspan="1">1 4 2 5 3 7 6</td> <td colname="3" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">reverse</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">lexicographic</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">order</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">on the | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">reverse</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">lexicographic</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">order</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">on the $ A ( i ) $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> <td colname="2" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">depth first</td> <td colname="2" style="background-color:white;" colspan="1">1 2 3 6 5 7 4</td> <td colname="3" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">lexicographic</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">order</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">on the | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">lexicographic</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">order</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">on the $ A ( i ) $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> <td colname="2" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">depth first</td> <td colname="2" style="background-color:white;" colspan="1">1 4 5 7 2 3 6</td> <td colname="3" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">reverse</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">lexicographic</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">order</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">on the | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">reverse</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">lexicographic</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">order</td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">on the $ A ( i ) $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"></td> </tr> </tbody> </table> | ||
</td></tr> </table> | </td></tr> </table> | ||
| − | There is an obvious analogous search algorithm for non-oriented graphs. These algorithms run in | + | There is an obvious analogous search algorithm for non-oriented graphs. These algorithms run in $ O ( \# V + \# E ) $ |
| + | time. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.K. Ahuja, T.L. Magnanti, J.B. Orlin, "Network flows" G.L. Nemhauser (ed.) A.H.G. Rinnooy Kan (ed.) M.J. Todd (ed.) , ''Optimization'' , North-Holland (1991) pp. 211–370</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> H.M. Salkin, "Integer programming" , Addison-Wesley (1975)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> C.H. Papadimitriou, K. Steiglitz, "Combinatorial optimization" , Prentice-Hall (1982)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> A.A. Zhigljavsky, "Theory of global random search" , Kluwer Acad. Publ. (1991) (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.K. Ahuja, T.L. Magnanti, J.B. Orlin, "Network flows" G.L. Nemhauser (ed.) A.H.G. Rinnooy Kan (ed.) M.J. Todd (ed.) , ''Optimization'' , North-Holland (1991) pp. 211–370</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> H.M. Salkin, "Integer programming" , Addison-Wesley (1975)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> C.H. Papadimitriou, K. Steiglitz, "Combinatorial optimization" , Prentice-Hall (1982)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> A.A. Zhigljavsky, "Theory of global random search" , Kluwer Acad. Publ. (1991) (In Russian)</TD></TR></table> | ||
Latest revision as of 08:12, 6 June 2020
on a graph, graph search
An algorithm that tries to find all nodes in a network or graph that satisfy a given property. Such algorithms are also used, e.g., to optimize a function on a graph or network or on a set which can easily be turned into a graph, such as $ \{ 0,1 \} ^ {n} $. (Two $ 0 $- $ 1 $ vectors of length $ n $ are joined if an only if they differ in precisely one coordinate, yielding a hypercube.) Thus, these are definite relations and similarities between graph search and search theory as a systematic optimization technique (of enumeration type) [a3]. See [a4] for a very complete overview of global optimization (from the search point of view, including random search).
Two of the most often used search techniques in graphs or networks are depth-first search and breadth-first search. Let $ \Gamma = ( V,E ) $ be a finite oriented graph (cf. Graph, oriented). For each $ v \in V $, let $ A ( v ) $ be the set of edges (arcs) issuing from $ v $. For instance, in Fig.a1, $ A ( 1 ) = \{ ( 1,2 ) , ( 1,4 ) \} $, $ A ( 3 ) = \{ ( 3,6 ) \} $, $ A ( 7 ) = \emptyset $.
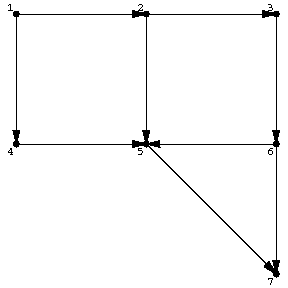
Figure: s110070a
It is assumed that the sets $ A ( v ) $, $ v \in V $, are given some fixed total order (cf. also Totally ordered set) for all $ v $. The following algorithm picks out all nodes in $ \Gamma $ that are reachable from a source node $ s $ by means of a directed path. These nodes will be marked. Central to the algorithm is a certain list $ L $, which can be seen as a sort of wave front indicating the boundary of the spreading blob of marked points:
unmark all points;
mark the source node $ s $;
set $ L = \{ s \} $;
as long as $ L $ is non-empty, run the following iterative procedure:
choose a node $ i \in L $;
select the first oriented edge $ ( i,j ) \in A ( i ) $ that runs (from $ i $) to an unmarked node $ j $( if any);
mark the node $ j $;
define the function $ { \mathop{\rm revp} } $ on $ j $ as $ { \mathop{\rm revp} } ( j ) = i $;
add $ j $ to $ L $;
if there is no $ ( i,j ) \in A ( i ) $ that runs to an unmarked node $ j $, remove $ i $ from $ L $.
stop when $ L $ is empty.
The algorithm does not yet specify how to select a node from $ L $. If $ L $ is treated as a queue, i.e., the node selected is the one that has been longest in $ L $( first-in-first-out) the result is breadth-first search. On the other hand, if $ L $ is treated as a stack, i.e., the node selected is the one that was last added to $ L $( last-in-first-out) the result is depth-first search.
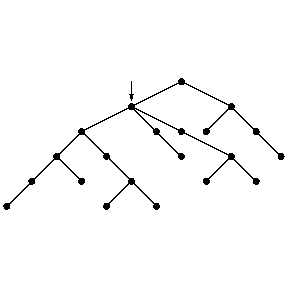
Figure: s110070b
For an oriented tree as in Fig.a2 (downwards oriented), starting at the indicated node, breadth-first search will first pick the three children of the node indicated (in some order) and then will proceed to the next layer. Depth-first search will first pick a maximal downward chain (maximal in the sense that it ends at a leaf, not necessarily maximal in length) and then go back to another child of the last branching node in that chain.
The order which is used on the edge sets $ A ( v ) $ also matters, but not as much.
The edges picked out by the function $ { \mathop{\rm revp} } $( reverse path), i.e., the edges $ ( { \mathop{\rm revp} } ( j ) ,j ) $ form an oriented tree comprising the reachable nodes from the source node $ s $.
The results of the algorithm in four cases are given below for the case of Fig.a1.
<tbody> </tbody>
|
There is an obvious analogous search algorithm for non-oriented graphs. These algorithms run in $ O ( \# V + \# E ) $ time.
References
| [a1] | R.K. Ahuja, T.L. Magnanti, J.B. Orlin, "Network flows" G.L. Nemhauser (ed.) A.H.G. Rinnooy Kan (ed.) M.J. Todd (ed.) , Optimization , North-Holland (1991) pp. 211–370 |
| [a2] | H.M. Salkin, "Integer programming" , Addison-Wesley (1975) |
| [a3] | C.H. Papadimitriou, K. Steiglitz, "Combinatorial optimization" , Prentice-Hall (1982) |
| [a4] | A.A. Zhigljavsky, "Theory of global random search" , Kluwer Acad. Publ. (1991) (In Russian) |
Search algorithm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Search_algorithm&oldid=48636