|
|
| Line 1: |
Line 1: |
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s1100401.png" /> be a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s1100402.png" />-dimensional [[Differentiable manifold|differentiable manifold]] of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s1100403.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s1100404.png" /> be a tensor field of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s1100405.png" /> (cf. also [[Tensor on a vector space|Tensor on a vector space]]), a [[Vector field|vector field]] and a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s1100406.png" />-form on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s1100407.png" /> (cf. [[Differential form|Differential form]]), respectively, such that
| + | <!-- |
| | + | s1100401.png |
| | + | $#A+1 = 108 n = 1 |
| | + | $#C+1 = 108 : ~/encyclopedia/old_files/data/S110/S.1100040 Sasakian manifold |
| | + | Automatically converted into TeX, above some diagnostics. |
| | + | Please remove this comment and the {{TEX|auto}} line below, |
| | + | if TeX found to be correct. |
| | + | --> |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s1100408.png" /></td> </tr></table>
| + | {{TEX|auto}} |
| | + | {{TEX|done}} |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s1100409.png" /> is the identity on the [[Tangent bundle|tangent bundle]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004010.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004011.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004012.png" /> is said to be an almost contact structure on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004013.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004014.png" /> is called an almost contact manifold. If follows that
| + | Let $ M $ |
| | + | be a $ ( 2m + 1 ) $- |
| | + | dimensional [[Differentiable manifold|differentiable manifold]] of class $ C ^ \infty $ |
| | + | and let $ \phi, \xi, \eta $ |
| | + | be a tensor field of type $ ( 1,1 ) $( |
| | + | cf. also [[Tensor on a vector space|Tensor on a vector space]]), a [[Vector field|vector field]] and a $ 1 $- |
| | + | form on $ M $( |
| | + | cf. [[Differential form|Differential form]]), respectively, such that |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004015.png" /></td> </tr></table>
| + | $$ |
| | + | \phi ^ {2} = - I + \eta \otimes \xi, \quad \eta ( \xi ) = 1, |
| | + | $$ |
| | | | |
| − | and therefore <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004016.png" /> has the constant rank <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004017.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004018.png" />. Moreover, there exists a [[Riemannian metric|Riemannian metric]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004019.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004020.png" /> such that
| + | where $ I $ |
| | + | is the identity on the [[Tangent bundle|tangent bundle]] $ TM $ |
| | + | of $ M $. |
| | + | Then $ ( \phi, \xi, \eta ) $ |
| | + | is said to be an almost contact structure on $ M $, |
| | + | and $ M $ |
| | + | is called an almost contact manifold. If follows that |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004021.png" /></td> </tr></table>
| + | $$ |
| | + | \eta \circ \phi = 0, \quad \phi ( \xi ) = 0, |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004022.png" /></td> </tr></table>
| + | and therefore $ \phi $ |
| | + | has the constant rank $ 2m $ |
| | + | on $ M $. |
| | + | Moreover, there exists a [[Riemannian metric|Riemannian metric]] $ g $ |
| | + | on $ M $ |
| | + | such that |
| | | | |
| − | for any vector fields <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004023.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004024.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004025.png" /> [[#References|[a2]]]. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004026.png" /> is said to be an almost contact metric structure and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004027.png" /> an almost contact metric manifold. On <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004028.png" /> one defines the fundamental <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004030.png" />-form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004031.png" /> by
| + | $$ |
| | + | g ( \phi x, \phi Y ) = g ( X,Y ) - \eta ( X ) \eta ( Y ) , |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004032.png" /></td> </tr></table>
| + | $$ |
| | + | \eta ( X ) = g ( X, \xi ) , |
| | + | $$ |
| | | | |
| − | Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004033.png" /> is said to be a contact metric structure on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004034.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004035.png" />. | + | for any vector fields $ X $, |
| | + | $ Y $ |
| | + | on $ M $[[#References|[a2]]]. Then $ ( \phi, \xi, \eta,g ) $ |
| | + | is said to be an almost contact metric structure and $ M $ |
| | + | an almost contact metric manifold. On $ M $ |
| | + | one defines the fundamental $ 2 $- |
| | + | form $ \Phi $ |
| | + | by |
| | | | |
| − | The Nijenhuis tensor field of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004036.png" /> is the tensor field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004037.png" /> of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004038.png" /> given by
| + | $$ |
| | + | \Phi ( X,Y ) = g ( X, \phi Y ) . |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004039.png" /></td> </tr></table>
| + | Then $ ( \phi, \xi, \eta,g ) $ |
| | + | is said to be a contact metric structure on $ M $ |
| | + | if $ \Phi = d \eta $. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004040.png" /></td> </tr></table>
| + | The Nijenhuis tensor field of $ \phi $ |
| | + | is the tensor field $ [ \phi, \phi] $ |
| | + | of type $ ( 1,2 ) $ |
| | + | given by |
| | | | |
| − | The almost contact structure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004041.png" /> is said to be normal if
| + | $$ |
| | + | [ \phi, \phi ] ( X,Y ) = \phi ^ {2} [ X,Y ] - [ \phi X, \phi Y ] + |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004042.png" /></td> </tr></table>
| + | $$ |
| | + | - \phi [ \phi X,Y ] - \phi [ X, \phi Y ] . |
| | + | $$ |
| | | | |
| − | A manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004043.png" /> endowed with a normal contact metric structure is called a Sasakian manifold. To study Sasakian manifolds one often uses the following characterization (cf. [[#References|[a4]]]): An almost contact metric manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004044.png" /> is Sasakian if and only if
| + | The almost contact structure $ ( \phi, \xi, \eta ) $ |
| | + | is said to be normal if |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004045.png" /></td> </tr></table>
| + | $$ |
| | + | [ \phi, \phi ] + 2d \eta \otimes \xi = 0. |
| | + | $$ |
| | | | |
| − | for any vector fields <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004046.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004047.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004048.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004049.png" /> is the [[Levi-Civita connection|Levi-Civita connection]] on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004050.png" /> with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004051.png" />.
| + | A manifold $ M $ |
| | + | endowed with a normal contact metric structure is called a Sasakian manifold. To study Sasakian manifolds one often uses the following characterization (cf. [[#References|[a4]]]): An almost contact metric manifold $ M $ |
| | + | is Sasakian if and only if |
| | | | |
| − | A plane section <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004052.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004053.png" /> is called a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004055.png" />-section if there exists a unit vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004056.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004057.png" /> orthogonal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004058.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004059.png" /> is an orthonormal basis of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004060.png" />. The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004062.png" />-sectional curvature of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004063.png" /> with respect to a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004064.png" />-section <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004065.png" /> is defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004066.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004067.png" /> is the curvature tensor field of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004068.png" />. When the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004069.png" />-sectional curvature does not depend on both the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004070.png" /> and the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004071.png" />-section <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004072.png" />, one says that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004073.png" /> has constant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004075.png" />-sectional curvature and calls it a Sasakian space form. | + | $$ |
| | + | ( \nabla _ {X} \phi ) Y = g ( X,Y ) \xi - \eta ( Y ) X, |
| | + | $$ |
| | + | |
| | + | for any vector fields $ X $, |
| | + | $ Y $ |
| | + | on $ M $, |
| | + | where $ \nabla $ |
| | + | is the [[Levi-Civita connection|Levi-Civita connection]] on $ M $ |
| | + | with respect to $ g $. |
| | + | |
| | + | A plane section $ \pi $ |
| | + | in $ T _ {x} M $ |
| | + | is called a $ \phi $- |
| | + | section if there exists a unit vector $ X $ |
| | + | in $ T _ {x} M $ |
| | + | orthogonal to $ \xi $ |
| | + | such that $ \{ X, \phi X \} $ |
| | + | is an orthonormal basis of $ \pi $. |
| | + | The $ \phi $- |
| | + | sectional curvature of $ M $ |
| | + | with respect to a $ \phi $- |
| | + | section $ \pi $ |
| | + | is defined by $ H ( \pi ) = g ( R ( X, \phi X ) \phi X,X ) $, |
| | + | where $ R $ |
| | + | is the curvature tensor field of $ \nabla $. |
| | + | When the $ \phi $- |
| | + | sectional curvature does not depend on both the point $ x \in M $ |
| | + | and the $ \phi $- |
| | + | section $ \pi $, |
| | + | one says that $ M $ |
| | + | has constant $ \phi $- |
| | + | sectional curvature and calls it a Sasakian space form. |
| | | | |
| | General references for Sasakian manifolds are [[#References|[a2]]], [[#References|[a3]]], [[#References|[a6]]]. | | General references for Sasakian manifolds are [[#References|[a2]]], [[#References|[a3]]], [[#References|[a6]]]. |
| | | | |
| | ==Submanifolds of Sasakian manifolds.== | | ==Submanifolds of Sasakian manifolds.== |
| − | Three classes of submanifolds of a Sasakian manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004076.png" /> have been studied intensively. | + | Three classes of submanifolds of a Sasakian manifold $ M $ |
| | + | have been studied intensively. |
| | | | |
| − | First, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004077.png" /> be a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004078.png" />-dimensional submanifold of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004079.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004080.png" /> is tangent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004081.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004082.png" />, for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004083.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004084.png" /> is said to be an invariant submanifold of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004085.png" />. It follows that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004086.png" /> is a Sasakian manifold too, and, in general, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004087.png" /> inherits the properties of the ambient Sasakian manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004088.png" />. | + | First, let $ N $ |
| | + | be a $ ( 2n + 1 ) $- |
| | + | dimensional submanifold of $ M $ |
| | + | such that $ \xi $ |
| | + | is tangent to $ N $ |
| | + | and $ \phi ( T _ {x} N ) \subset T _ {x} N $, |
| | + | for all $ x \in N $. |
| | + | Then $ N $ |
| | + | is said to be an invariant submanifold of $ M $. |
| | + | It follows that $ N $ |
| | + | is a Sasakian manifold too, and, in general, $ N $ |
| | + | inherits the properties of the ambient Sasakian manifold $ M $. |
| | | | |
| − | Next, an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004089.png" />-dimensional submanifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004090.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004091.png" /> is an anti-invariant submanifold if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004092.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004093.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004094.png" /> is the normal space of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004095.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004096.png" />. The most important results on anti-invariant submanifolds have been collected in [[#References|[a5]]]. | + | Next, an $ n $- |
| | + | dimensional submanifold $ N $ |
| | + | of $ M $ |
| | + | is an anti-invariant submanifold if $ \phi ( T _ {x} N ) \subset T _ {x} N ^ \perp $ |
| | + | for all $ x \in N $, |
| | + | where $ T _ {x} N ^ \perp $ |
| | + | is the normal space of $ N $ |
| | + | at $ x $. |
| | + | The most important results on anti-invariant submanifolds have been collected in [[#References|[a5]]]. |
| | | | |
| − | Finally, an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004097.png" />-dimensional submanifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004098.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s11004099.png" /> is said to be a semi-invariant submanifold (a contact CR-submanifold; cf. also [[CR-submanifold|CR-submanifold]]) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s110040100.png" /> is tangent to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s110040101.png" /> and there exist two distributions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s110040102.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s110040103.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s110040104.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s110040105.png" /> has the orthogonal decomposition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s110040106.png" />, with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s110040107.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s110040108.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s110040109.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s110040110.png" /> denotes the distribution spanned by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s110040111.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s110040112.png" />. For the geometry of semi-invariant submanifolds, see [[#References|[a1]]]. | + | Finally, an $ n $- |
| | + | dimensional submanifold $ N $ |
| | + | of $ M $ |
| | + | is said to be a semi-invariant submanifold (a contact CR-submanifold; cf. also [[CR-submanifold|CR-submanifold]]) if $ \xi $ |
| | + | is tangent to $ N $ |
| | + | and there exist two distributions $ D $ |
| | + | and $ D ^ \perp $ |
| | + | on $ N $ |
| | + | such that $ TN $ |
| | + | has the orthogonal decomposition $ TN = D \oplus D ^ \perp \oplus \{ \xi \} $, |
| | + | with $ \phi ( D _ {x} ) = D _ {x} $ |
| | + | and $ \phi ( D _ {x} ^ \perp ) \subset T _ {x} N ^ \perp $ |
| | + | for all $ x \in N $, |
| | + | where $ \{ \xi \} $ |
| | + | denotes the distribution spanned by $ \xi $ |
| | + | on $ N $. |
| | + | For the geometry of semi-invariant submanifolds, see [[#References|[a1]]]. |
| | | | |
| | ====References==== | | ====References==== |
| | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Bejancu, "Geometry of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s110040113.png" /> submanifolds" , Reidel (1986)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> D.E. Blair, "Contact manifolds in Riemannian geometry" , ''Lecture Notes in Mathematics'' , '''509''' , Springer (1976)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> S. Sasaki, "Almost contact manifolds" , ''Lecture Notes'' , '''1–3''' , Math. Inst. Tôhoku Univ. (1965–1968)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> S. Sasaki, Y. Hatakeyama, "On differentiable manifolds with contact metric strctures" ''J. Math. Soc. Japan'' , '''14''' (1962) pp. 249–271</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> K. Yano, M. Kon, "Anti-invariant submanifolds" , M. Dekker (1976)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> K. Yano, M. Kon, "Structures on manifolds" , World Sci. (1984)</TD></TR></table> | | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A. Bejancu, "Geometry of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s110/s110040/s110040113.png" /> submanifolds" , Reidel (1986)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> D.E. Blair, "Contact manifolds in Riemannian geometry" , ''Lecture Notes in Mathematics'' , '''509''' , Springer (1976)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> S. Sasaki, "Almost contact manifolds" , ''Lecture Notes'' , '''1–3''' , Math. Inst. Tôhoku Univ. (1965–1968)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> S. Sasaki, Y. Hatakeyama, "On differentiable manifolds with contact metric strctures" ''J. Math. Soc. Japan'' , '''14''' (1962) pp. 249–271</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> K. Yano, M. Kon, "Anti-invariant submanifolds" , M. Dekker (1976)</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> K. Yano, M. Kon, "Structures on manifolds" , World Sci. (1984)</TD></TR></table> |
Let $ M $
be a $ ( 2m + 1 ) $-
dimensional differentiable manifold of class $ C ^ \infty $
and let $ \phi, \xi, \eta $
be a tensor field of type $ ( 1,1 ) $(
cf. also Tensor on a vector space), a vector field and a $ 1 $-
form on $ M $(
cf. Differential form), respectively, such that
$$
\phi ^ {2} = - I + \eta \otimes \xi, \quad \eta ( \xi ) = 1,
$$
where $ I $
is the identity on the tangent bundle $ TM $
of $ M $.
Then $ ( \phi, \xi, \eta ) $
is said to be an almost contact structure on $ M $,
and $ M $
is called an almost contact manifold. If follows that
$$
\eta \circ \phi = 0, \quad \phi ( \xi ) = 0,
$$
and therefore $ \phi $
has the constant rank $ 2m $
on $ M $.
Moreover, there exists a Riemannian metric $ g $
on $ M $
such that
$$
g ( \phi x, \phi Y ) = g ( X,Y ) - \eta ( X ) \eta ( Y ) ,
$$
$$
\eta ( X ) = g ( X, \xi ) ,
$$
for any vector fields $ X $,
$ Y $
on $ M $[a2]. Then $ ( \phi, \xi, \eta,g ) $
is said to be an almost contact metric structure and $ M $
an almost contact metric manifold. On $ M $
one defines the fundamental $ 2 $-
form $ \Phi $
by
$$
\Phi ( X,Y ) = g ( X, \phi Y ) .
$$
Then $ ( \phi, \xi, \eta,g ) $
is said to be a contact metric structure on $ M $
if $ \Phi = d \eta $.
The Nijenhuis tensor field of $ \phi $
is the tensor field $ [ \phi, \phi] $
of type $ ( 1,2 ) $
given by
$$
[ \phi, \phi ] ( X,Y ) = \phi ^ {2} [ X,Y ] - [ \phi X, \phi Y ] +
$$
$$
- \phi [ \phi X,Y ] - \phi [ X, \phi Y ] .
$$
The almost contact structure $ ( \phi, \xi, \eta ) $
is said to be normal if
$$
[ \phi, \phi ] + 2d \eta \otimes \xi = 0.
$$
A manifold $ M $
endowed with a normal contact metric structure is called a Sasakian manifold. To study Sasakian manifolds one often uses the following characterization (cf. [a4]): An almost contact metric manifold $ M $
is Sasakian if and only if
$$
( \nabla _ {X} \phi ) Y = g ( X,Y ) \xi - \eta ( Y ) X,
$$
for any vector fields $ X $,
$ Y $
on $ M $,
where $ \nabla $
is the Levi-Civita connection on $ M $
with respect to $ g $.
A plane section $ \pi $
in $ T _ {x} M $
is called a $ \phi $-
section if there exists a unit vector $ X $
in $ T _ {x} M $
orthogonal to $ \xi $
such that $ \{ X, \phi X \} $
is an orthonormal basis of $ \pi $.
The $ \phi $-
sectional curvature of $ M $
with respect to a $ \phi $-
section $ \pi $
is defined by $ H ( \pi ) = g ( R ( X, \phi X ) \phi X,X ) $,
where $ R $
is the curvature tensor field of $ \nabla $.
When the $ \phi $-
sectional curvature does not depend on both the point $ x \in M $
and the $ \phi $-
section $ \pi $,
one says that $ M $
has constant $ \phi $-
sectional curvature and calls it a Sasakian space form.
General references for Sasakian manifolds are [a2], [a3], [a6].
Submanifolds of Sasakian manifolds.
Three classes of submanifolds of a Sasakian manifold $ M $
have been studied intensively.
First, let $ N $
be a $ ( 2n + 1 ) $-
dimensional submanifold of $ M $
such that $ \xi $
is tangent to $ N $
and $ \phi ( T _ {x} N ) \subset T _ {x} N $,
for all $ x \in N $.
Then $ N $
is said to be an invariant submanifold of $ M $.
It follows that $ N $
is a Sasakian manifold too, and, in general, $ N $
inherits the properties of the ambient Sasakian manifold $ M $.
Next, an $ n $-
dimensional submanifold $ N $
of $ M $
is an anti-invariant submanifold if $ \phi ( T _ {x} N ) \subset T _ {x} N ^ \perp $
for all $ x \in N $,
where $ T _ {x} N ^ \perp $
is the normal space of $ N $
at $ x $.
The most important results on anti-invariant submanifolds have been collected in [a5].
Finally, an $ n $-
dimensional submanifold $ N $
of $ M $
is said to be a semi-invariant submanifold (a contact CR-submanifold; cf. also CR-submanifold) if $ \xi $
is tangent to $ N $
and there exist two distributions $ D $
and $ D ^ \perp $
on $ N $
such that $ TN $
has the orthogonal decomposition $ TN = D \oplus D ^ \perp \oplus \{ \xi \} $,
with $ \phi ( D _ {x} ) = D _ {x} $
and $ \phi ( D _ {x} ^ \perp ) \subset T _ {x} N ^ \perp $
for all $ x \in N $,
where $ \{ \xi \} $
denotes the distribution spanned by $ \xi $
on $ N $.
For the geometry of semi-invariant submanifolds, see [a1].
References
| [a1] | A. Bejancu, "Geometry of 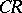 submanifolds" , Reidel (1986) submanifolds" , Reidel (1986) |
| [a2] | D.E. Blair, "Contact manifolds in Riemannian geometry" , Lecture Notes in Mathematics , 509 , Springer (1976) |
| [a3] | S. Sasaki, "Almost contact manifolds" , Lecture Notes , 1–3 , Math. Inst. Tôhoku Univ. (1965–1968) |
| [a4] | S. Sasaki, Y. Hatakeyama, "On differentiable manifolds with contact metric strctures" J. Math. Soc. Japan , 14 (1962) pp. 249–271 |
| [a5] | K. Yano, M. Kon, "Anti-invariant submanifolds" , M. Dekker (1976) |
| [a6] | K. Yano, M. Kon, "Structures on manifolds" , World Sci. (1984) |
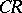 submanifolds" , Reidel (1986)
submanifolds" , Reidel (1986)