Difference between revisions of "Recurrent point"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | r0801901.png | ||
| + | $#A+1 = 43 n = 0 | ||
| + | $#C+1 = 43 : ~/encyclopedia/old_files/data/R080/R.0800190 Recurrent point | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''of a dynamical system'' | ''of a dynamical system'' | ||
| − | A point | + | A point $ x $ |
| + | of a [[Dynamical system|dynamical system]] $ f ^ { t } $( | ||
| + | also denoted by $ f( t, \cdot ) $, | ||
| + | see [[#References|[2]]]) in a metric space $ S $ | ||
| + | that satisfies the following condition: For any $ \epsilon > 0 $ | ||
| + | there exists a $ T > 0 $ | ||
| + | such that all points of the trajectory $ f ^ { t } x $ | ||
| + | are contained in an $ \epsilon $- | ||
| + | neighbourhood of any arc of time length $ T $ | ||
| + | of this trajectory (in other words, with any $ \tau \in \mathbf R $, | ||
| + | the $ \epsilon $- | ||
| + | neighbourhood of the set | ||
| − | + | $$ | |
| + | \{ {f ^ { t } x } : {t \in [ \tau , \tau + T ] } \} | ||
| + | $$ | ||
| − | contains all of the trajectory | + | contains all of the trajectory $ f ^ { t } x $). |
| + | In this case $ f ^ { t } x $ | ||
| + | is called a recurrent trajectory. | ||
| − | Birkhoff's theorem: If the space | + | Birkhoff's theorem: If the space $ S $ |
| + | is complete (e.g. $ S = \mathbf R ^ {n} $), | ||
| + | then: 1) for a point to be recurrent it is necessary and sufficient that the closure of its trajectory be a compact [[Minimal set|minimal set]]; and 2) for the existence of a recurrent point it is sufficient that there be a point that is stable according to Lagrange (see [[Lagrange stability|Lagrange stability]]). | ||
| − | A recurrent point is stable according to Poisson (see [[Poisson stability|Poisson stability]]), and if the space | + | A recurrent point is stable according to Poisson (see [[Poisson stability|Poisson stability]]), and if the space $ S $ |
| + | is complete, also stable according to Lagrange (see [[Lagrange stability|Lagrange stability]]). An almost-periodic (in particular, a fixed or periodic) point of a dynamical system is recurrent. In general, any point of a strictly ergodic dynamical system (in a complete space) is recurrent, but the restriction of a dynamical system to the closure of a recurrent trajectory (a minimal set) need not be a strictly ergodic dynamical system (Markov's example, see [[#References|[2]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> G.D. Birkhoff, "Dynamical systems" , Amer. Math. Soc. (1927)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G.D. Birkhoff, "Dynamical systems" , Amer. Math. Soc. (1927)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | An almost-periodic point of a dynamical system | + | An almost-periodic point of a dynamical system $ f ^ { t } $ |
| + | on a metric space $ ( S , \rho ) $ | ||
| + | is a point $ x \in G $ | ||
| + | with the following property: For every $ \epsilon > 0 $ | ||
| + | the set | ||
| − | + | $$ | |
| + | AP ( x, \epsilon ) = \{ {t \in \mathbf R } : { | ||
| + | \rho ( f ^ { s+ t } ( x), f ^ { s } ( x) ) < \epsilon \ | ||
| + | \textrm{ for all } s \in \mathbf R } \} | ||
| + | $$ | ||
| − | is relatively dense in | + | is relatively dense in $ \mathbf R $, |
| + | i.e., there exists a length $ l ( \epsilon ) $ | ||
| + | such that every interval in $ \mathbf R $ | ||
| + | with length $ h \geq l ( \epsilon ) $ | ||
| + | contains a point of $ AP( x, \epsilon ) $. | ||
| + | (Thus, one might say that the function $ t \mapsto f ^ { t } ( x) : \mathbf R \rightarrow S $ | ||
| + | is almost-periodic; cf. [[Almost-period|Almost-period]].) | ||
| − | Another important notion is that of an almost-recurrent point: A point | + | Another important notion is that of an almost-recurrent point: A point $ x \in S $ |
| + | such that for every $ \epsilon > 0 $ | ||
| + | the set | ||
| − | + | $$ | |
| + | R( x , U _ \epsilon ) = \ | ||
| + | \{ {t \in \mathbf R } : {f ^ { t } ( x) \in U _ \epsilon } \} | ||
| + | $$ | ||
| − | is relatively dense in | + | is relatively dense in $ \mathbf R $, |
| + | where $ U _ \epsilon $ | ||
| + | is the open $ \epsilon $- | ||
| + | ball around $ x $. | ||
| + | (This definition can easily be generalized to the case of a flow or a cascade on an arbitrary topological space.) The relationship of these notions with that of a recurrent point, Birkhoff's theorem and a number of other implications can be visualized as follows: | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r080190a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/r080190a.gif" /> | ||
| Line 33: | Line 84: | ||
Figure: r080190a | Figure: r080190a | ||
| − | Here the implication indicated by the dotted arrow holds only in a complete space, and | + | Here the implication indicated by the dotted arrow holds only in a complete space, and $ \Sigma _ {x} $ |
| + | denotes the closure of the trajectory of $ x $. | ||
| + | The property "Sx is Lyapunov stable rel(ative) Sx" means that the family $ \{ f ^ { t } \mid _ {\Sigma _ {x} } \} _ {t \in \mathbf R } $ | ||
| + | of functions from $ \Sigma _ {x} $ | ||
| + | into $ \Sigma _ {x} $ | ||
| + | is equicontinuous on $ \Sigma _ {x} $( | ||
| + | see [[Lyapunov stability|Lyapunov stability]]). For a refinement of this diagram (including the notions of a pseudo-recurrent point and a uniformly Poisson-stable trajectory) see [[#References|[a3]]]. | ||
| − | In the literature on topological dynamics (in particular, in the literature directly or indirectly influenced by [[#References|[a2]]]) another terminology is in use: | + | In the literature on topological dynamics (in particular, in the literature directly or indirectly influenced by [[#References|[a2]]]) another terminology is in use:<table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1">Above, [[#References|[2]]], [[#References|[a3]]]</td> <td colname="2" style="background-color:white;" colspan="1">[[#References|[a2]]]</td> <td colname="3" style="background-color:white;" colspan="1">[[#References|[a1]]]</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">almost periodic</td> <td colname="2" style="background-color:white;" colspan="1">—</td> <td colname="3" style="background-color:white;" colspan="1">—</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">recurrent</td> <td colname="2" style="background-color:white;" colspan="1">—</td> <td colname="3" style="background-color:white;" colspan="1">—</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">almost recurrent</td> <td colname="2" style="background-color:white;" colspan="1">almost periodic</td> <td colname="3" style="background-color:white;" colspan="1">uniformly recurrent</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">Poisson-stable</td> <td colname="2" style="background-color:white;" colspan="1">recurrent</td> <td colname="3" style="background-color:white;" colspan="1">recurrent</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">(non-) wandering</td> <td colname="2" style="background-color:white;" colspan="1">(not) regionally recurrent</td> <td colname="3" style="background-color:white;" colspan="1">—</td> </tr> </tbody> </table> |
</td></tr> </table> | </td></tr> </table> | ||
| − | (To be precise, in [[#References|[a1]]] "recurrent" means positive Poisson stable, i.e., | + | (To be precise, in [[#References|[a1]]] "recurrent" means positive Poisson stable, i.e., $ x $ |
| + | belongs only to the $ \omega $- | ||
| + | limit set of its own trajectory.) | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Furstenberg, "Recurrence in ergodic theory and combinatorial number theory" , Princeton Univ. Press (1981)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W.H. Gottschalk, G.A. Hedlund, "Topological dynamics" , Amer. Math. Soc. (1955)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> K.S. [K.S. Sibirskii] Sibirsky, "Introduction to topological dynamics" , Noordhoff (1975) (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Furstenberg, "Recurrence in ergodic theory and combinatorial number theory" , Princeton Univ. Press (1981)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> W.H. Gottschalk, G.A. Hedlund, "Topological dynamics" , Amer. Math. Soc. (1955)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> K.S. [K.S. Sibirskii] Sibirsky, "Introduction to topological dynamics" , Noordhoff (1975) (Translated from Russian)</TD></TR></table> | ||
Revision as of 08:10, 6 June 2020
of a dynamical system
A point $ x $ of a dynamical system $ f ^ { t } $( also denoted by $ f( t, \cdot ) $, see [2]) in a metric space $ S $ that satisfies the following condition: For any $ \epsilon > 0 $ there exists a $ T > 0 $ such that all points of the trajectory $ f ^ { t } x $ are contained in an $ \epsilon $- neighbourhood of any arc of time length $ T $ of this trajectory (in other words, with any $ \tau \in \mathbf R $, the $ \epsilon $- neighbourhood of the set
$$ \{ {f ^ { t } x } : {t \in [ \tau , \tau + T ] } \} $$
contains all of the trajectory $ f ^ { t } x $). In this case $ f ^ { t } x $ is called a recurrent trajectory.
Birkhoff's theorem: If the space $ S $ is complete (e.g. $ S = \mathbf R ^ {n} $), then: 1) for a point to be recurrent it is necessary and sufficient that the closure of its trajectory be a compact minimal set; and 2) for the existence of a recurrent point it is sufficient that there be a point that is stable according to Lagrange (see Lagrange stability).
A recurrent point is stable according to Poisson (see Poisson stability), and if the space $ S $ is complete, also stable according to Lagrange (see Lagrange stability). An almost-periodic (in particular, a fixed or periodic) point of a dynamical system is recurrent. In general, any point of a strictly ergodic dynamical system (in a complete space) is recurrent, but the restriction of a dynamical system to the closure of a recurrent trajectory (a minimal set) need not be a strictly ergodic dynamical system (Markov's example, see [2]).
References
| [1] | G.D. Birkhoff, "Dynamical systems" , Amer. Math. Soc. (1927) |
| [2] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) |
Comments
An almost-periodic point of a dynamical system $ f ^ { t } $ on a metric space $ ( S , \rho ) $ is a point $ x \in G $ with the following property: For every $ \epsilon > 0 $ the set
$$ AP ( x, \epsilon ) = \{ {t \in \mathbf R } : { \rho ( f ^ { s+ t } ( x), f ^ { s } ( x) ) < \epsilon \ \textrm{ for all } s \in \mathbf R } \} $$
is relatively dense in $ \mathbf R $, i.e., there exists a length $ l ( \epsilon ) $ such that every interval in $ \mathbf R $ with length $ h \geq l ( \epsilon ) $ contains a point of $ AP( x, \epsilon ) $. (Thus, one might say that the function $ t \mapsto f ^ { t } ( x) : \mathbf R \rightarrow S $ is almost-periodic; cf. Almost-period.)
Another important notion is that of an almost-recurrent point: A point $ x \in S $ such that for every $ \epsilon > 0 $ the set
$$ R( x , U _ \epsilon ) = \ \{ {t \in \mathbf R } : {f ^ { t } ( x) \in U _ \epsilon } \} $$
is relatively dense in $ \mathbf R $, where $ U _ \epsilon $ is the open $ \epsilon $- ball around $ x $. (This definition can easily be generalized to the case of a flow or a cascade on an arbitrary topological space.) The relationship of these notions with that of a recurrent point, Birkhoff's theorem and a number of other implications can be visualized as follows:
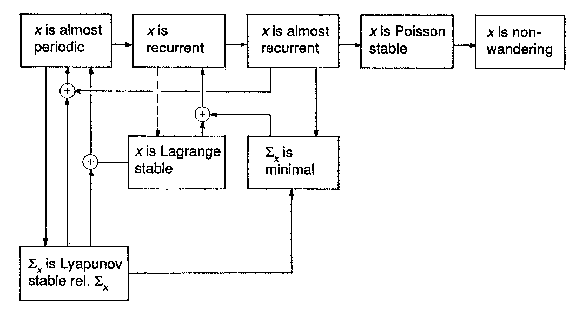
Figure: r080190a
Here the implication indicated by the dotted arrow holds only in a complete space, and $ \Sigma _ {x} $ denotes the closure of the trajectory of $ x $. The property "Sx is Lyapunov stable rel(ative) Sx" means that the family $ \{ f ^ { t } \mid _ {\Sigma _ {x} } \} _ {t \in \mathbf R } $ of functions from $ \Sigma _ {x} $ into $ \Sigma _ {x} $ is equicontinuous on $ \Sigma _ {x} $( see Lyapunov stability). For a refinement of this diagram (including the notions of a pseudo-recurrent point and a uniformly Poisson-stable trajectory) see [a3].
In the literature on topological dynamics (in particular, in the literature directly or indirectly influenced by [a2]) another terminology is in use:
<tbody> </tbody>
|
(To be precise, in [a1] "recurrent" means positive Poisson stable, i.e., $ x $ belongs only to the $ \omega $- limit set of its own trajectory.)
References
| [a1] | H. Furstenberg, "Recurrence in ergodic theory and combinatorial number theory" , Princeton Univ. Press (1981) |
| [a2] | W.H. Gottschalk, G.A. Hedlund, "Topological dynamics" , Amer. Math. Soc. (1955) |
| [a3] | K.S. [K.S. Sibirskii] Sibirsky, "Introduction to topological dynamics" , Noordhoff (1975) (Translated from Russian) |
Recurrent point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Recurrent_point&oldid=48455