Difference between revisions of "Positive element"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | p0739201.png | ||
| + | $#A+1 = 20 n = 2 | ||
| + | $#C+1 = 20 : ~/encyclopedia/old_files/data/P073/P.0703920 Positive element | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | An element | + | {{TEX|auto}} |
| + | {{TEX|done}} | ||
| + | |||
| + | ''of an algebra $ A $ | ||
| + | with an involution $ {} ^ {*} $'' | ||
| + | |||
| + | An element $ x $ | ||
| + | of $ A $ | ||
| + | of the form $ x = y ^ {*} y $, | ||
| + | where $ y \in A $. | ||
| + | The set $ P( A) $ | ||
| + | of positive elements in a Banach $ * $- | ||
| + | algebra $ A $ | ||
| + | contains the set $ Q( A) $ | ||
| + | of squares of the Hermitian elements, which in turn contains the set $ P _ {0} ( A) ^ {+} $ | ||
| + | of all Hermitian elements with positive spectrum (cf. [[Spectrum of an element|Spectrum of an element]]), but in general it does not contain the set $ A ^ {+} $ | ||
| + | of all Hermitian elements with non-negative spectrum. The condition $ P( A) \subset A ^ {+} $ | ||
| + | defines the class of completely-symmetric (or Hermitian) Banach $ * $- | ||
| + | algebras. For a $ * $- | ||
| + | algebra to be completely symmetric it is necessary and sufficient that all Hermitian elements in it have real spectrum. The equality $ P( A) = A ^ {+} $ | ||
| + | holds if and only if $ A $ | ||
| + | is a [[C*-algebra| $ C ^ {*} $- | ||
| + | algebra]]. In that case $ P( A) $ | ||
| + | is a reproducing cone (cf. [[Semi-ordered space|Semi-ordered space]]) in the space of all Hermitian elements of the algebra $ A $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J. Dixmier, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073920/p07392021.png" /> algebras" , North-Holland (1977) (Translated from French)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> D.N. Raikov, ''Dokl. Akad. Nauk. SSSR'' , '''54''' : 5 (1946) pp. 391–394</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V. Pták, "On the spectral radius in Banach algebras with involution" ''Bull. London Math. Soc.'' , '''2''' (1970) pp. 327–334</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> T.W. Palmer, "Hermitian Banach <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073920/p07392022.png" />-algebras" ''Bull. Amer. Math. Soc.'' , '''78''' (1972) pp. 522–524</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J. Dixmier, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073920/p07392021.png" /> algebras" , North-Holland (1977) (Translated from French)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> D.N. Raikov, ''Dokl. Akad. Nauk. SSSR'' , '''54''' : 5 (1946) pp. 391–394</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V. Pták, "On the spectral radius in Banach algebras with involution" ''Bull. London Math. Soc.'' , '''2''' (1970) pp. 327–334</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> T.W. Palmer, "Hermitian Banach <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073920/p07392022.png" />-algebras" ''Bull. Amer. Math. Soc.'' , '''78''' (1972) pp. 522–524</TD></TR></table> | ||
Latest revision as of 08:07, 6 June 2020
of an algebra $ A $
with an involution $ {} ^ {*} $
An element $ x $ of $ A $ of the form $ x = y ^ {*} y $, where $ y \in A $. The set $ P( A) $ of positive elements in a Banach $ * $- algebra $ A $ contains the set $ Q( A) $ of squares of the Hermitian elements, which in turn contains the set $ P _ {0} ( A) ^ {+} $ of all Hermitian elements with positive spectrum (cf. Spectrum of an element), but in general it does not contain the set $ A ^ {+} $ of all Hermitian elements with non-negative spectrum. The condition $ P( A) \subset A ^ {+} $ defines the class of completely-symmetric (or Hermitian) Banach $ * $- algebras. For a $ * $- algebra to be completely symmetric it is necessary and sufficient that all Hermitian elements in it have real spectrum. The equality $ P( A) = A ^ {+} $ holds if and only if $ A $ is a $ C ^ {*} $- algebra. In that case $ P( A) $ is a reproducing cone (cf. Semi-ordered space) in the space of all Hermitian elements of the algebra $ A $.
References
| [1] | M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian) |
| [2] | J. Dixmier, "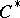 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
| [3] | D.N. Raikov, Dokl. Akad. Nauk. SSSR , 54 : 5 (1946) pp. 391–394 |
| [4] | V. Pták, "On the spectral radius in Banach algebras with involution" Bull. London Math. Soc. , 2 (1970) pp. 327–334 |
| [5] | T.W. Palmer, "Hermitian Banach  -algebras" Bull. Amer. Math. Soc. , 78 (1972) pp. 522–524 -algebras" Bull. Amer. Math. Soc. , 78 (1972) pp. 522–524 |
Positive element. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Positive_element&oldid=48253