Difference between revisions of "Pontryagin space"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | p0738001.png | ||
| + | $#A+1 = 98 n = 2 | ||
| + | $#C+1 = 98 : ~/encyclopedia/old_files/data/P073/P.0703800 Pontryagin space | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A [[Hilbert space with an indefinite metric|Hilbert space with an indefinite metric]] $ \Pi _ \kappa $ | |
| + | that has a finite rank of indefiniteness $ \kappa $. | ||
| + | Basic facts concerning the geometry of these spaces were established by L.S. Pontryagin [[#References|[1]]]. Besides the facts common for spaces with an indefinite metric, the following properties hold. | ||
| − | + | If $ {\mathcal P} $ | |
| + | is an arbitrary non-negative linear manifold in $ \Pi _ \kappa $, | ||
| + | then $ \mathop{\rm dim} {\mathcal P} \leq \kappa $; | ||
| + | if $ {\mathcal P} $ | ||
| + | is a positive linear manifold and $ \mathop{\rm dim} {\mathcal P} = \kappa $, | ||
| + | then its $ J $- | ||
| + | orthogonal complement $ N $ | ||
| + | is a negative linear manifold and $ \Pi _ \kappa = {\mathcal P} \oplus N $. | ||
| + | Moreover, $ N $ | ||
| + | is a complete space with respect to the norm $ | x | = \sqrt {- J ( x , x ) } $. | ||
| + | If the linear manifold $ L \subset \Pi _ \kappa $ | ||
| + | is non-degenerate, then its $ J $- | ||
| + | orthogonal complement $ M $ | ||
| + | is non-degenerate as well and $ \Pi _ \kappa = M \oplus L $. | ||
| − | + | The spectrum (in particular, the discrete spectrum) of a $ J $- | |
| + | unitary ( $ J $- | ||
| + | self-adjoint) operator is symmetric with respect to the unit circle (real line), all elementary divisors corresponding to eigen values $ \lambda $, | ||
| + | $ | \lambda | > 1 $, | ||
| + | are of finite order $ \rho _ \lambda $, | ||
| + | $ \rho _ \lambda \leq \kappa $, | ||
| + | $ \rho _ \lambda = - \rho _ {\lambda ^ {-} 1 } $. | ||
| + | The sum of the dimensions of the root subspaces of a $ J $- | ||
| + | unitary ( $ J $- | ||
| + | self-adjoint) operator corresponding to eigen values $ \lambda $, | ||
| + | $ | \lambda | > 1 $( | ||
| + | $ \mathop{\rm lm} \lambda > 0 $), | ||
| + | does not exceed $ \kappa $. | ||
| − | + | The following theorem [[#References|[1]]] is fundamental in the theory of $ J $- | |
| + | self-adjoint operators on a Pontryagin space $ \Pi _ \kappa $: | ||
| + | For each $ J $- | ||
| + | self-adjoint operator $ A $( | ||
| + | $ \overline{ {D ( A) }}\; = \Pi _ \kappa $) | ||
| + | there exists a $ \kappa $- | ||
| + | dimensional (maximal) non-negative invariant subspace $ {\mathcal T} $ | ||
| + | in which all eigen values of $ A $ | ||
| + | have non-negative imaginary parts, and a $ \kappa $- | ||
| + | dimensional non-negative invariant subspace $ {\mathcal T} ^ \prime $ | ||
| + | in which all eigen values have non-positive imaginary parts. A similar statement in which the upper (lower) half-plane is replaced by the exterior (interior) of the unit disc is also valid for $ J $- | ||
| + | unitary operators, and under certain additional conditions — even for operators on the space $ \Pi _ \infty $. | ||
| − | + | If $ U $ | |
| + | is a $ J $- | ||
| + | unitary operator, then its maximal invariant subspaces $ {\mathcal T} $, | ||
| + | $ {\mathcal T} ^ \prime $ | ||
| + | can be chosen so that the elementary divisors of the operator $ U _ {\mathcal T} = U \mid _ {\mathcal T} $, | ||
| + | $ U _ { {\mathcal T} ^ \prime } = U \mid _ { {\mathcal T} ^ \prime } $ | ||
| + | are of minimal order. In order that a polynomial $ P ( \lambda ) $ | ||
| + | with no roots inside the unit disc has the property: $ ( P ( U) x , P ( U) x ) \leq 0 $, | ||
| + | $ x \in \Pi _ \kappa $, | ||
| + | it is necessary and sufficient that it can be divided by the minimal annihilating polynomial of the operator $ U _ {\mathcal T} $. | ||
| + | If $ U $ | ||
| + | is a cyclic operator, then its non-negative invariant subspaces of dimension $ \kappa $ | ||
| + | are uniquely determined. In this case the above-mentioned property of the polynomial $ P $ | ||
| + | with roots $ \{ \lambda _ {i} \} $ | ||
| + | outside the unit disc, $ | \lambda _ {i} | > 1 $, | ||
| + | is equivalent to the divisibility of $ P ( \lambda ) $ | ||
| + | by the characteristic polynomial of $ U _ {\mathcal T} $. | ||
| − | + | Each completely-continuous $ J $- | |
| + | self-adjoint operator $ A $ | ||
| + | on a Pontryagin space $ \Pi _ \kappa $ | ||
| + | such that zero belongs to its continuous spectrum does not have a residual spectrum. The root vectors of such an operator form a [[Riesz basis|Riesz basis]] in $ \Pi _ \kappa $ | ||
| + | with respect to the (definite) norm $ ( | J | x , x ) $. | ||
| + | |||
| + | Many facts concerning invariant subspaces and the spectrum can be generalized to a case of $ J $- | ||
| + | isometric and $ J $- | ||
| + | non-expanding operators. Thus, if $ \lambda _ {1} \dots \lambda _ {n} $ | ||
| + | is an arbitrary set of eigen values of a $ J $- | ||
| + | isometric operator, $ \lambda _ {i} \overline \lambda \; _ {k} \neq 1 $, | ||
| + | $ i , k = 1 \dots n $, | ||
| + | and if $ \rho _ {i} $ | ||
| + | is the order of the elementary divisor at the point $ \lambda _ {i} $, | ||
| + | then $ \sum _ {1} ^ {n} \rho _ {i} \leq \kappa $. | ||
| + | Any $ J $- | ||
| + | non-expanding boundedly-invertible operator $ T $ | ||
| + | has a $ \kappa $- | ||
| + | dimensional invariant non-negative subspace $ {\mathcal T} $ | ||
| + | such that all eigen values of the restriction $ T \mid _ {\mathcal T} $ | ||
| + | lie in the unit disc [[#References|[2]]]. A similar fact holds for maximal $ J $- | ||
| + | dissipative operators. In general, a $ J $- | ||
| + | dissipative operator $ A $, | ||
| + | $ D ( A) \subset D ( A ^ {*} ) $, | ||
| + | has at most $ \kappa $ | ||
| + | eigen values in the upper half-plane. $ J $- | ||
| + | isometric and $ J $- | ||
| + | symmetric (and more generally, $ J $- | ||
| + | non-expanding and $ J $- | ||
| + | dissipative) operators are related by the Cayley transformation (cf. [[Cayley transform|Cayley transform]]), which has on $ \Pi _ \kappa $ | ||
| + | all natural properties [[#References|[2]]]. This fact allows one to develop the extension theory simultaneously for $ J $- | ||
| + | isometric and $ J $- | ||
| + | symmetric operators. In particular, every $ J $- | ||
| + | isometric ( $ J $- | ||
| + | symmetric) operator can be extended to a maximal one. If its deficiency indices are different, then it has no $ J $- | ||
| + | unitary ( $ J $- | ||
| + | self-adjoint) extensions. If these indices are equal and finite, then any maximal extension is $ J $- | ||
| + | unitary ( $ J $- | ||
| + | self-adjoint). | ||
| + | |||
| + | For completely-continuous operators on $ \Pi _ \kappa $, | ||
| + | a number of statements on the completeness of the system of root vectors, analogous to the corresponding facts from the theory of dissipative operators on spaces with a definite metric, is valid. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.S. Pontryagin, "Hermitian operators in a space with indefinite metric" ''Izv. Akad. Nauk. SSSR Ser. Mat.'' , '''8''' (1944) pp. 243–280 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.S. Iokhvidov, M.G. Krein, "Spectral theory of operators in a space with indefinite metric I" ''Transl. Amer. Math. Soc. (2)'' , '''13''' (1960) pp. 105–175 ''Trudy Moskov. Mat. Obshch.'' , '''5''' (1956) pp. 367–432</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.S. Iokhvidov, M.G. Krein, "Spectral theory of operators in a space with indefinite metric II" ''Trudy Moskov. Mat. Obshch.'' , '''8''' (1959) pp. 413–496 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> T.Ya. Azizov, I.S. Iokhvidov, "Linear operators in Hilbert spaces with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073800/p073800102.png" />-metric" ''Russian Math. Surveys'' , '''26''' : 4 (1971) pp. 45–97 ''Uspekhi Mat. Nauk'' , '''26''' : 4 (1971) pp. 43–92</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M.G. Krein, "Introduction to the geometry of indefinite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073800/p073800103.png" />-spaces and the theory of operators in these spaces" , ''Second Math. Summer School'' , '''1''' , Kiev (1965) pp. 15–92 (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M.A. Naimark, R.S. Ismagilov, "Representations of groups and algebras in a space with indefinite metric" ''Itogi Nauk. i Tekhn. Mat. Anal.'' (1969) pp. 73–105 (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> L. Nagy, "State vector spaces with indefinite metric in quantum field theory" , Noordhoff (1966)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.S. Pontryagin, "Hermitian operators in a space with indefinite metric" ''Izv. Akad. Nauk. SSSR Ser. Mat.'' , '''8''' (1944) pp. 243–280 (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.S. Iokhvidov, M.G. Krein, "Spectral theory of operators in a space with indefinite metric I" ''Transl. Amer. Math. Soc. (2)'' , '''13''' (1960) pp. 105–175 ''Trudy Moskov. Mat. Obshch.'' , '''5''' (1956) pp. 367–432</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.S. Iokhvidov, M.G. Krein, "Spectral theory of operators in a space with indefinite metric II" ''Trudy Moskov. Mat. Obshch.'' , '''8''' (1959) pp. 413–496 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> T.Ya. Azizov, I.S. Iokhvidov, "Linear operators in Hilbert spaces with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073800/p073800102.png" />-metric" ''Russian Math. Surveys'' , '''26''' : 4 (1971) pp. 45–97 ''Uspekhi Mat. Nauk'' , '''26''' : 4 (1971) pp. 43–92</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M.G. Krein, "Introduction to the geometry of indefinite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073800/p073800103.png" />-spaces and the theory of operators in these spaces" , ''Second Math. Summer School'' , '''1''' , Kiev (1965) pp. 15–92 (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M.A. Naimark, R.S. Ismagilov, "Representations of groups and algebras in a space with indefinite metric" ''Itogi Nauk. i Tekhn. Mat. Anal.'' (1969) pp. 73–105 (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> L. Nagy, "State vector spaces with indefinite metric in quantum field theory" , Noordhoff (1966)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | Pontryagin spaces form a subclass of the class of Krein spaces (cf. [[Krein space|Krein space]] and also [[Hilbert space with an indefinite metric|Hilbert space with an indefinite metric]]). The operator | + | Pontryagin spaces form a subclass of the class of Krein spaces (cf. [[Krein space|Krein space]] and also [[Hilbert space with an indefinite metric|Hilbert space with an indefinite metric]]). The operator $ J $ |
| + | appearing in the beginning of the main article above is the fundamental symmetry (see [[Krein space|Krein space]]), which defines the indefinite inner product via the formula $ [ x, y] = ( Jx, y) $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> T.Ya. Azizov, I.S. [I.S. Iokhvidov] Iohidov, "Linear operators in spaces with an indefinite metric" , Wiley (1989) (Translated from Russian)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> I.S. [I.S. Iokhvidov] Iohidov, M.G. Krein, H. Langer, "Introduction to the spectral theory of operators in spaces with an indefinite metric" , Akademie Verlag (1982)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> T.Ya. Azizov, I.S. [I.S. Iokhvidov] Iohidov, "Linear operators in spaces with an indefinite metric" , Wiley (1989) (Translated from Russian)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> I.S. [I.S. Iokhvidov] Iohidov, M.G. Krein, H. Langer, "Introduction to the spectral theory of operators in spaces with an indefinite metric" , Akademie Verlag (1982)</TD></TR></table> | ||
Latest revision as of 08:07, 6 June 2020
A Hilbert space with an indefinite metric $ \Pi _ \kappa $
that has a finite rank of indefiniteness $ \kappa $.
Basic facts concerning the geometry of these spaces were established by L.S. Pontryagin [1]. Besides the facts common for spaces with an indefinite metric, the following properties hold.
If $ {\mathcal P} $ is an arbitrary non-negative linear manifold in $ \Pi _ \kappa $, then $ \mathop{\rm dim} {\mathcal P} \leq \kappa $; if $ {\mathcal P} $ is a positive linear manifold and $ \mathop{\rm dim} {\mathcal P} = \kappa $, then its $ J $- orthogonal complement $ N $ is a negative linear manifold and $ \Pi _ \kappa = {\mathcal P} \oplus N $. Moreover, $ N $ is a complete space with respect to the norm $ | x | = \sqrt {- J ( x , x ) } $. If the linear manifold $ L \subset \Pi _ \kappa $ is non-degenerate, then its $ J $- orthogonal complement $ M $ is non-degenerate as well and $ \Pi _ \kappa = M \oplus L $.
The spectrum (in particular, the discrete spectrum) of a $ J $- unitary ( $ J $- self-adjoint) operator is symmetric with respect to the unit circle (real line), all elementary divisors corresponding to eigen values $ \lambda $, $ | \lambda | > 1 $, are of finite order $ \rho _ \lambda $, $ \rho _ \lambda \leq \kappa $, $ \rho _ \lambda = - \rho _ {\lambda ^ {-} 1 } $. The sum of the dimensions of the root subspaces of a $ J $- unitary ( $ J $- self-adjoint) operator corresponding to eigen values $ \lambda $, $ | \lambda | > 1 $( $ \mathop{\rm lm} \lambda > 0 $), does not exceed $ \kappa $.
The following theorem [1] is fundamental in the theory of $ J $- self-adjoint operators on a Pontryagin space $ \Pi _ \kappa $: For each $ J $- self-adjoint operator $ A $( $ \overline{ {D ( A) }}\; = \Pi _ \kappa $) there exists a $ \kappa $- dimensional (maximal) non-negative invariant subspace $ {\mathcal T} $ in which all eigen values of $ A $ have non-negative imaginary parts, and a $ \kappa $- dimensional non-negative invariant subspace $ {\mathcal T} ^ \prime $ in which all eigen values have non-positive imaginary parts. A similar statement in which the upper (lower) half-plane is replaced by the exterior (interior) of the unit disc is also valid for $ J $- unitary operators, and under certain additional conditions — even for operators on the space $ \Pi _ \infty $.
If $ U $ is a $ J $- unitary operator, then its maximal invariant subspaces $ {\mathcal T} $, $ {\mathcal T} ^ \prime $ can be chosen so that the elementary divisors of the operator $ U _ {\mathcal T} = U \mid _ {\mathcal T} $, $ U _ { {\mathcal T} ^ \prime } = U \mid _ { {\mathcal T} ^ \prime } $ are of minimal order. In order that a polynomial $ P ( \lambda ) $ with no roots inside the unit disc has the property: $ ( P ( U) x , P ( U) x ) \leq 0 $, $ x \in \Pi _ \kappa $, it is necessary and sufficient that it can be divided by the minimal annihilating polynomial of the operator $ U _ {\mathcal T} $. If $ U $ is a cyclic operator, then its non-negative invariant subspaces of dimension $ \kappa $ are uniquely determined. In this case the above-mentioned property of the polynomial $ P $ with roots $ \{ \lambda _ {i} \} $ outside the unit disc, $ | \lambda _ {i} | > 1 $, is equivalent to the divisibility of $ P ( \lambda ) $ by the characteristic polynomial of $ U _ {\mathcal T} $.
Each completely-continuous $ J $- self-adjoint operator $ A $ on a Pontryagin space $ \Pi _ \kappa $ such that zero belongs to its continuous spectrum does not have a residual spectrum. The root vectors of such an operator form a Riesz basis in $ \Pi _ \kappa $ with respect to the (definite) norm $ ( | J | x , x ) $.
Many facts concerning invariant subspaces and the spectrum can be generalized to a case of $ J $- isometric and $ J $- non-expanding operators. Thus, if $ \lambda _ {1} \dots \lambda _ {n} $ is an arbitrary set of eigen values of a $ J $- isometric operator, $ \lambda _ {i} \overline \lambda \; _ {k} \neq 1 $, $ i , k = 1 \dots n $, and if $ \rho _ {i} $ is the order of the elementary divisor at the point $ \lambda _ {i} $, then $ \sum _ {1} ^ {n} \rho _ {i} \leq \kappa $. Any $ J $- non-expanding boundedly-invertible operator $ T $ has a $ \kappa $- dimensional invariant non-negative subspace $ {\mathcal T} $ such that all eigen values of the restriction $ T \mid _ {\mathcal T} $ lie in the unit disc [2]. A similar fact holds for maximal $ J $- dissipative operators. In general, a $ J $- dissipative operator $ A $, $ D ( A) \subset D ( A ^ {*} ) $, has at most $ \kappa $ eigen values in the upper half-plane. $ J $- isometric and $ J $- symmetric (and more generally, $ J $- non-expanding and $ J $- dissipative) operators are related by the Cayley transformation (cf. Cayley transform), which has on $ \Pi _ \kappa $ all natural properties [2]. This fact allows one to develop the extension theory simultaneously for $ J $- isometric and $ J $- symmetric operators. In particular, every $ J $- isometric ( $ J $- symmetric) operator can be extended to a maximal one. If its deficiency indices are different, then it has no $ J $- unitary ( $ J $- self-adjoint) extensions. If these indices are equal and finite, then any maximal extension is $ J $- unitary ( $ J $- self-adjoint).
For completely-continuous operators on $ \Pi _ \kappa $, a number of statements on the completeness of the system of root vectors, analogous to the corresponding facts from the theory of dissipative operators on spaces with a definite metric, is valid.
References
| [1] | L.S. Pontryagin, "Hermitian operators in a space with indefinite metric" Izv. Akad. Nauk. SSSR Ser. Mat. , 8 (1944) pp. 243–280 (In Russian) |
| [2] | I.S. Iokhvidov, M.G. Krein, "Spectral theory of operators in a space with indefinite metric I" Transl. Amer. Math. Soc. (2) , 13 (1960) pp. 105–175 Trudy Moskov. Mat. Obshch. , 5 (1956) pp. 367–432 |
| [3] | I.S. Iokhvidov, M.G. Krein, "Spectral theory of operators in a space with indefinite metric II" Trudy Moskov. Mat. Obshch. , 8 (1959) pp. 413–496 (In Russian) |
| [4] | T.Ya. Azizov, I.S. Iokhvidov, "Linear operators in Hilbert spaces with 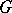 -metric" Russian Math. Surveys , 26 : 4 (1971) pp. 45–97 Uspekhi Mat. Nauk , 26 : 4 (1971) pp. 43–92 -metric" Russian Math. Surveys , 26 : 4 (1971) pp. 45–97 Uspekhi Mat. Nauk , 26 : 4 (1971) pp. 43–92 |
| [5] | M.G. Krein, "Introduction to the geometry of indefinite 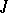 -spaces and the theory of operators in these spaces" , Second Math. Summer School , 1 , Kiev (1965) pp. 15–92 (In Russian) -spaces and the theory of operators in these spaces" , Second Math. Summer School , 1 , Kiev (1965) pp. 15–92 (In Russian) |
| [6] | M.A. Naimark, R.S. Ismagilov, "Representations of groups and algebras in a space with indefinite metric" Itogi Nauk. i Tekhn. Mat. Anal. (1969) pp. 73–105 (In Russian) |
| [7] | L. Nagy, "State vector spaces with indefinite metric in quantum field theory" , Noordhoff (1966) |
Comments
Pontryagin spaces form a subclass of the class of Krein spaces (cf. Krein space and also Hilbert space with an indefinite metric). The operator $ J $ appearing in the beginning of the main article above is the fundamental symmetry (see Krein space), which defines the indefinite inner product via the formula $ [ x, y] = ( Jx, y) $.
References
| [a1] | T.Ya. Azizov, I.S. [I.S. Iokhvidov] Iohidov, "Linear operators in spaces with an indefinite metric" , Wiley (1989) (Translated from Russian) |
| [a2] | I.S. [I.S. Iokhvidov] Iohidov, M.G. Krein, H. Langer, "Introduction to the spectral theory of operators in spaces with an indefinite metric" , Akademie Verlag (1982) |
Pontryagin space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pontryagin_space&oldid=48243