Difference between revisions of "Poisson integral"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | p0733301.png | ||
| + | $#A+1 = 84 n = 2 | ||
| + | $#C+1 = 84 : ~/encyclopedia/old_files/data/P073/P.0703330 Poisson integral | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | An integral representation of the solution of the [[Dirichlet problem|Dirichlet problem]] for the [[Laplace equation|Laplace equation]] in the simplest domains. Thus, the Poisson integral for the ball $ B _ {n} ( 0 , R ) $ | |
| + | in the Euclidean space $ \mathbf R ^ {n} $, | ||
| + | $ n \geq 2 $, | ||
| + | of radius $ R $ | ||
| + | and with centre at the coordinate origin has the form | ||
| − | + | $$ \tag{1 } | |
| + | u ( x) = \int\limits _ {S _ {n} ( 0 , R ) } | ||
| + | f ( y) P B _ {n} ( x , y ) d S _ {n} ( y) , | ||
| + | $$ | ||
| − | is the Poisson kernel for the ball, | + | where $ f $ |
| + | is a given continuous function on the sphere $ S _ {n} ( 0 , R ) $ | ||
| + | of radius $ R $, | ||
| + | |||
| + | $$ | ||
| + | P B _ {n} ( x , y ) = \ | ||
| + | |||
| + | \frac{1}{\sigma _ {n} } | ||
| + | |||
| + | \frac{R ^ {n-} 2 ( R ^ {2} - | x | ^ {2} ) }{| x - y | ^ {n} } | ||
| + | |||
| + | $$ | ||
| + | |||
| + | is the Poisson kernel for the ball, $ \sigma _ {n} = n \pi ^ {n/2} R ^ {n-} 1 / \Gamma ( 1 + n / 2 ) $ | ||
| + | is the area of the sphere $ S _ {n} ( 0 , R ) $, | ||
| + | and $ d S _ {n} $ | ||
| + | is the surface element on $ S _ {n} ( 0 , R ) $. | ||
S.D. Poisson | S.D. Poisson | ||
| − | arrived at formula (1) in the case | + | arrived at formula (1) in the case $ n = 2 $ |
| + | as an integral formula for the sum of the trigonometric series | ||
| + | |||
| + | $$ | ||
| + | |||
| + | \frac{a _ {0} }{2} | ||
| + | + | ||
| + | \sum _ { k= } 1 ^ \infty | ||
| + | ( a _ {k} \cos k \theta + b _ {k} \sin k \theta ) | ||
| + | r ^ {k} , | ||
| + | $$ | ||
| − | + | where $ a _ {k} $, | |
| + | $ b _ {k} $ | ||
| + | are the Fourier coefficients of the function $ f ( y) = f ( e ^ {i \phi } ) $, | ||
| + | and $ ( r , \theta ) $ | ||
| + | and $ ( 1 , \phi ) $ | ||
| + | are the polar coordinates of the points $ x = r e ^ {i \theta } $ | ||
| + | and $ y = e ^ {i \phi } $, | ||
| + | respectively; in this case the Poisson kernel has the form | ||
| − | + | $$ \tag{2 } | |
| + | P B _ {2} ( x , y ) = \ | ||
| + | P B _ {2} ( r e ^ {i \theta } , e ^ {i \phi } ) = \ | ||
| − | + | \frac{1}{2 \pi } | |
| + | |||
| + | \frac{1 - r ^ {2} }{1 - 2 r \cos ( \theta - \phi ) + r ^ {2} } | ||
| + | |||
| + | $$ | ||
(for applications of the Poisson integral in the theory of trigonometric series see [[#References|[3]]] and also [[Abel–Poisson summation method|Abel–Poisson summation method]]). | (for applications of the Poisson integral in the theory of trigonometric series see [[#References|[3]]] and also [[Abel–Poisson summation method|Abel–Poisson summation method]]). | ||
| Line 23: | Line 77: | ||
The Poisson integral for the half-space | The Poisson integral for the half-space | ||
| − | + | $$ | |
| + | \mathbf R _ {+} ^ {n} = \ | ||
| + | \{ {x = ( x _ {1} \dots x _ {n} ) \in \mathbf R ^ {n} } : {x _ {n} > 0 } \} | ||
| + | $$ | ||
has the form | has the form | ||
| − | + | $$ \tag{3 } | |
| + | u ( x) = \int\limits _ {\mathbf R _ {0} ^ {n} } | ||
| + | f ( y) P R _ {+} ^ {n} ( x , y ) d R _ {0} ^ {n} ( y) , | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | \mathbf R _ {0} ^ {n} = \ | ||
| + | \{ {y = ( y _ {1} \dots y _ {n} ) \in \mathbf R ^ {n} } : {y _ {n} = 0 } \} | ||
| + | , | ||
| + | $$ | ||
| + | |||
| + | $ d R _ {0} ^ {n} $ | ||
| + | is the volume element in $ \mathbf R _ {0} ^ {n} $, | ||
| + | $ f $ | ||
| + | is a bounded continuous function on $ \mathbf R _ {0} ^ {n} $ | ||
| + | and | ||
| + | |||
| + | $$ | ||
| + | P R _ {+} ^ {n} ( x , y ) = \ | ||
| − | + | \frac{2 \Gamma ( 1 + n/2) }{n \pi ^ {n/2} } | |
| − | + | \frac{x _ {n} }{| x - y | ^ {n} } | |
| + | |||
| + | $$ | ||
is the Poisson kernel for the half-space. The formulas (1) and (3) are particular cases of the Green formula | is the Poisson kernel for the half-space. The formulas (1) and (3) are particular cases of the Green formula | ||
| − | + | $$ \tag{4 } | |
| + | u ( x) = \int\limits _ \Gamma f ( y) | ||
| − | + | \frac{\partial G ( x , y ) }{\partial n _ {y} } | |
| + | \ | ||
| + | d \Gamma ( y) , | ||
| + | $$ | ||
| − | + | giving the solution of the Dirichlet problem for domains $ D \subset \mathbf R ^ {n} $ | |
| + | with smooth boundary $ \Gamma $ | ||
| + | using the derivative $ \partial G ( x , y ) / \partial n _ {y} $ | ||
| + | of the Green function $ G ( x , y ) $ | ||
| + | in the direction of the interior normal to $ \Gamma $ | ||
| + | at the point $ y \in \Gamma $. | ||
| + | Sometimes formula (4) is also called the Poisson integral. | ||
| − | The Poisson integral | + | The basic properties of the Poisson integral are: 1) $ u ( x) $ |
| + | is a [[Harmonic function|harmonic function]] of the coordinates of the point $ x $; | ||
| + | and 2) the Poisson integral gives the solution of the Dirichlet problem with boundary data $ f $ | ||
| + | in the class of (bounded) harmonic functions, that is, the function $ u ( x) $ | ||
| + | extended to the boundary of the domain by the values $ f ( y) $ | ||
| + | is continuous in the closed domain. Applications of the Poisson integral in classical mathematical physics are based on these properties (see [[#References|[4]]]). | ||
| − | + | The Poisson integral understood in the sense of Lebesgue when $ f $ | |
| + | is a summable function, for example on $ S _ {n} ( 0 , R ) $, | ||
| + | is called a Poisson–Lebesgue integral; an integral of the form | ||
| − | with respect to an arbitrary finite [[Borel measure|Borel measure]] | + | $$ \tag{5 } |
| + | u ( x) = \int\limits _ {S _ {n} ( 0 , R ) } | ||
| + | P B _ {n} ( x , y ) d \mu ( y) | ||
| + | $$ | ||
| + | |||
| + | with respect to an arbitrary finite [[Borel measure|Borel measure]] $ \mu $ | ||
| + | concentrated on $ S _ {n} ( 0 , R ) $ | ||
| + | is called a Poisson–Stieltjes integral. The class $ A $ | ||
| + | of harmonic functions $ u $ | ||
| + | representable by an integral (5) is characterized by the fact that any function $ u \in A $ | ||
| + | is the difference of two non-negative harmonic functions in $ B _ {n} ( 0 , R ) $. | ||
| + | The class of functions representable by a Poisson–Lebesgue integral is a proper subclass of the class $ A $ | ||
| + | and contains all bounded harmonic functions in $ B _ {n} ( 0 , R ) $. | ||
| + | For almost-all points $ y \in S _ {n} ( 0 , R ) $ | ||
| + | with respect to Lebesgue measure on $ S _ {n} ( 0 , R ) $, | ||
| + | a Poisson–Stieltjes integral (5) has angular boundary values coinciding with the values of the derivative $ \mu ^ \prime ( y) $ | ||
| + | of the measure $ \mu $ | ||
| + | with respect to Lebesgue measure. The theory of Poisson–Stieltjes and Poisson–Lebesgue integrals has also been constructed for the half-space (see [[#References|[5]]]). | ||
Various modifications of the Poisson integral play a large role in the theory of analytic functions of several complex variables and in its applications to quantum field theory. For example, the Poisson kernel for the polydisc | Various modifications of the Poisson integral play a large role in the theory of analytic functions of several complex variables and in its applications to quantum field theory. For example, the Poisson kernel for the polydisc | ||
| − | + | $$ | |
| + | U ^ {n} = \{ {z = ( z _ {1} \dots z _ {n} ) \in \mathbf C ^ {n} } : { | ||
| + | | z _ {j} | < 1 , j = 1 \dots n } \} | ||
| + | $$ | ||
| − | in the complex space | + | in the complex space $ \mathbf C ^ {n} $ |
| + | is obtained by multiplying the kernels (2): | ||
| − | + | $$ | |
| + | P U ^ {n} ( z , \zeta ) \ | ||
| + | = \prod _ { j= } 1 ^ { n } P B _ {2} ( z _ {j} , \zeta _ {j} ) . | ||
| + | $$ | ||
The corresponding Poisson integral | The corresponding Poisson integral | ||
| − | + | $$ | |
| + | u ( z) = \int\limits _ {T ^ {n} } | ||
| + | f ( \zeta ) P U ^ {n} ( z , \zeta ) d T ^ {n} ( \zeta ) | ||
| + | $$ | ||
| − | with respect to the distinguished boundary | + | with respect to the distinguished boundary $ T ^ {n} = \{ {\zeta = ( \zeta _ {1} \dots \zeta _ {n} ) \in \mathbf C ^ {n} } : {| \zeta _ {j} | = 1, j = 1 \dots n } \} $ |
| + | of the polydisc gives a multi-harmonic function $ u ( z) $, | ||
| + | $ z \in U ^ {n} $, | ||
| + | taking the continuous values $ f ( \zeta ) $ | ||
| + | on $ T ^ {n} $. | ||
| + | Generalizations in the form of Poisson–Lebesgue and Poisson–Stieltjes integrals are also considered (see [[#References|[6]]]). | ||
| − | In quantum field theory Poisson integrals are also applied to tube domains | + | In quantum field theory Poisson integrals are also applied to tube domains $ T ^ {C} $ |
| + | in the complex space $ \mathbf C ^ {n} $ | ||
| + | over a convex open acute cone $ C $ | ||
| + | in the space $ \mathbf R ^ {n} $( | ||
| + | with vertex at the origin). These have the form | ||
| − | + | $$ | |
| + | T ^ {C} = \mathbf R ^ {n} + i C = | ||
| + | $$ | ||
| − | + | $$ | |
| + | = \ | ||
| + | \{ z = x + i y \in \mathbf C ^ {n} : x = ( | ||
| + | x _ {1} \dots x _ {n} ) \in \mathbf R ^ {n} : y | ||
| + | = ( y _ {1} \dots y _ {n} ) \in C \} . | ||
| + | $$ | ||
| − | A Poisson integral of the form (3) for the half-plane when | + | A Poisson integral of the form (3) for the half-plane when $ n = 2 $ |
| + | is a particular case of such Poisson integrals for tube domains; the Poisson integral for bounded symmetric domains in the space $ \mathbf C ^ {n} $ | ||
| + | is the same as the Poisson integral for a tube domain in the space of matrices. Taking the density of the Poisson integral $ f $ | ||
| + | to be a generalized function and the Poisson integral itself to be the convolution of $ f $ | ||
| + | with the Poisson kernel one arrives at the important concept of the Poisson integral for certain classes of generalized functions (see [[#References|[7]]]–[[#References|[9]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1a]</TD> <TD valign="top"> S.D. Poisson, ''J. Ecole R. Polytechn.'' , '''11''' (1820) pp. 295–341</TD></TR><TR><TD valign="top">[1b]</TD> <TD valign="top"> S.D. Poisson, "Suite du mémoire sur les intégrales définies et sur la sommation des séries" ''J. Ecole R. Polytechn.'' , '''12''' (1823) pp. 404–509</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H.A. Schwarz, "Ueber die Integration der partiellen Differentialgleichung <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073330/p07333078.png" /> für die Fläche eines Kreises" ''Vierteljahrsschr. Naturforsch. Ges. Zurich'' , '''15''' (1870) pp. 113–128</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.N. Tikhonov, A.A. Samarskii, "Equations of mathematical physics" , Pergamon (1963) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E.D. Solomentsev, "Harmonic and subharmonic functions and their generalizations" ''Itogi Nauk. Mat. Anal. Teor. Veroyatnost. Regulirovanie. 1962'' (1964) pp. 83–100 (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> W. Rudin, "Function theory in polydiscs" , Benjamin (1969)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> V.S. Vladimirov, "Generalized functions in mathematical physics" , MIR (1979) (Translated from Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> L.K. Hua, "Harmonic analysis of functions of several complex variables in the classical domains" , Amer. Math. Soc. (1963) (Translated from Russian)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> E.M. Stein, G. Weiss, "Introduction to Fourier analysis on Euclidean spaces" , Princeton Univ. Press (1971)</TD></TR></table> | <table><TR><TD valign="top">[1a]</TD> <TD valign="top"> S.D. Poisson, ''J. Ecole R. Polytechn.'' , '''11''' (1820) pp. 295–341</TD></TR><TR><TD valign="top">[1b]</TD> <TD valign="top"> S.D. Poisson, "Suite du mémoire sur les intégrales définies et sur la sommation des séries" ''J. Ecole R. Polytechn.'' , '''12''' (1823) pp. 404–509</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H.A. Schwarz, "Ueber die Integration der partiellen Differentialgleichung <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073330/p07333078.png" /> für die Fläche eines Kreises" ''Vierteljahrsschr. Naturforsch. Ges. Zurich'' , '''15''' (1870) pp. 113–128</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.N. Tikhonov, A.A. Samarskii, "Equations of mathematical physics" , Pergamon (1963) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E.D. Solomentsev, "Harmonic and subharmonic functions and their generalizations" ''Itogi Nauk. Mat. Anal. Teor. Veroyatnost. Regulirovanie. 1962'' (1964) pp. 83–100 (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> W. Rudin, "Function theory in polydiscs" , Benjamin (1969)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> V.S. Vladimirov, "Generalized functions in mathematical physics" , MIR (1979) (Translated from Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> L.K. Hua, "Harmonic analysis of functions of several complex variables in the classical domains" , Amer. Math. Soc. (1963) (Translated from Russian)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> E.M. Stein, G. Weiss, "Introduction to Fourier analysis on Euclidean spaces" , Princeton Univ. Press (1971)</TD></TR></table> | ||
| + | ====Comments==== | ||
| + | The Poisson kernel for the exterior of the ball $ B _ {n} ( 0, R) $ | ||
| + | is given by | ||
| + | $$ | ||
| + | PB _ {n} ^ {c} ( x, y) = \ | ||
| − | + | \frac{1}{\sigma _ {n} } | |
| − | + | R ^ {n-} 2 | |
| + | \left ( | ||
| + | \frac{| x | ^ {2} - R ^ {2} }{| x- y | ^ {n} } | ||
| + | + | ||
| − | + | \frac{1}{R ^ {n-} 2 } | |
| + | - | ||
| + | \frac{1}{| x | ^ {n-} 2 } | ||
| + | \right ) . | ||
| + | $$ | ||
| − | In case of the unit ball | + | In case of the unit ball $ B $ |
| + | in $ \mathbf C ^ {n} $, | ||
| + | there are several Poisson-type kernels, e.g. the classical one, solving the classical Dirichlet problem, and the invariant Poisson kernel, which is invariant under holomorphic automorphisms of the unit ball. It reads | ||
| − | + | $$ | |
| + | P( z, \zeta ) = | ||
| + | \frac{( 1- | z | ^ {2} ) }{| 1-\langle z, \zeta \rangle | ^ {2n} } | ||
| + | ,\ \ | ||
| + | z \in B ,\ \zeta \in \partial B, | ||
| + | $$ | ||
| − | where | + | where $ \langle z, \zeta \rangle = \sum _ {1} ^ {n} z _ {j} \zeta _ {j} $ |
| + | and $ | z | ^ {2} = \langle z, z \rangle $. | ||
| + | This is the analogue for the ball of the Poisson kernel with respect to the distinguished boundary of the polydisc, described above. The invariant Poisson kernel solves the Dirichlet problem for the so-called invariant Laplacian, see [[#References|[a1]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Rudin, "Function theory in the unit ball in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073330/p07333086.png" />" , Springer (1980)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Rudin, "Function theory in the unit ball in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p073/p073330/p07333086.png" />" , Springer (1980)</TD></TR></table> | ||
Revision as of 08:06, 6 June 2020
An integral representation of the solution of the Dirichlet problem for the Laplace equation in the simplest domains. Thus, the Poisson integral for the ball $ B _ {n} ( 0 , R ) $
in the Euclidean space $ \mathbf R ^ {n} $,
$ n \geq 2 $,
of radius $ R $
and with centre at the coordinate origin has the form
$$ \tag{1 } u ( x) = \int\limits _ {S _ {n} ( 0 , R ) } f ( y) P B _ {n} ( x , y ) d S _ {n} ( y) , $$
where $ f $ is a given continuous function on the sphere $ S _ {n} ( 0 , R ) $ of radius $ R $,
$$ P B _ {n} ( x , y ) = \ \frac{1}{\sigma _ {n} } \frac{R ^ {n-} 2 ( R ^ {2} - | x | ^ {2} ) }{| x - y | ^ {n} } $$
is the Poisson kernel for the ball, $ \sigma _ {n} = n \pi ^ {n/2} R ^ {n-} 1 / \Gamma ( 1 + n / 2 ) $ is the area of the sphere $ S _ {n} ( 0 , R ) $, and $ d S _ {n} $ is the surface element on $ S _ {n} ( 0 , R ) $.
S.D. Poisson
arrived at formula (1) in the case $ n = 2 $ as an integral formula for the sum of the trigonometric series
$$ \frac{a _ {0} }{2} + \sum _ { k= } 1 ^ \infty ( a _ {k} \cos k \theta + b _ {k} \sin k \theta ) r ^ {k} , $$
where $ a _ {k} $, $ b _ {k} $ are the Fourier coefficients of the function $ f ( y) = f ( e ^ {i \phi } ) $, and $ ( r , \theta ) $ and $ ( 1 , \phi ) $ are the polar coordinates of the points $ x = r e ^ {i \theta } $ and $ y = e ^ {i \phi } $, respectively; in this case the Poisson kernel has the form
$$ \tag{2 } P B _ {2} ( x , y ) = \ P B _ {2} ( r e ^ {i \theta } , e ^ {i \phi } ) = \ \frac{1}{2 \pi } \frac{1 - r ^ {2} }{1 - 2 r \cos ( \theta - \phi ) + r ^ {2} } $$
(for applications of the Poisson integral in the theory of trigonometric series see [3] and also Abel–Poisson summation method).
The Poisson integral for the half-space
$$ \mathbf R _ {+} ^ {n} = \ \{ {x = ( x _ {1} \dots x _ {n} ) \in \mathbf R ^ {n} } : {x _ {n} > 0 } \} $$
has the form
$$ \tag{3 } u ( x) = \int\limits _ {\mathbf R _ {0} ^ {n} } f ( y) P R _ {+} ^ {n} ( x , y ) d R _ {0} ^ {n} ( y) , $$
where
$$ \mathbf R _ {0} ^ {n} = \ \{ {y = ( y _ {1} \dots y _ {n} ) \in \mathbf R ^ {n} } : {y _ {n} = 0 } \} , $$
$ d R _ {0} ^ {n} $ is the volume element in $ \mathbf R _ {0} ^ {n} $, $ f $ is a bounded continuous function on $ \mathbf R _ {0} ^ {n} $ and
$$ P R _ {+} ^ {n} ( x , y ) = \ \frac{2 \Gamma ( 1 + n/2) }{n \pi ^ {n/2} } \frac{x _ {n} }{| x - y | ^ {n} } $$
is the Poisson kernel for the half-space. The formulas (1) and (3) are particular cases of the Green formula
$$ \tag{4 } u ( x) = \int\limits _ \Gamma f ( y) \frac{\partial G ( x , y ) }{\partial n _ {y} } \ d \Gamma ( y) , $$
giving the solution of the Dirichlet problem for domains $ D \subset \mathbf R ^ {n} $ with smooth boundary $ \Gamma $ using the derivative $ \partial G ( x , y ) / \partial n _ {y} $ of the Green function $ G ( x , y ) $ in the direction of the interior normal to $ \Gamma $ at the point $ y \in \Gamma $. Sometimes formula (4) is also called the Poisson integral.
The basic properties of the Poisson integral are: 1) $ u ( x) $ is a harmonic function of the coordinates of the point $ x $; and 2) the Poisson integral gives the solution of the Dirichlet problem with boundary data $ f $ in the class of (bounded) harmonic functions, that is, the function $ u ( x) $ extended to the boundary of the domain by the values $ f ( y) $ is continuous in the closed domain. Applications of the Poisson integral in classical mathematical physics are based on these properties (see [4]).
The Poisson integral understood in the sense of Lebesgue when $ f $ is a summable function, for example on $ S _ {n} ( 0 , R ) $, is called a Poisson–Lebesgue integral; an integral of the form
$$ \tag{5 } u ( x) = \int\limits _ {S _ {n} ( 0 , R ) } P B _ {n} ( x , y ) d \mu ( y) $$
with respect to an arbitrary finite Borel measure $ \mu $ concentrated on $ S _ {n} ( 0 , R ) $ is called a Poisson–Stieltjes integral. The class $ A $ of harmonic functions $ u $ representable by an integral (5) is characterized by the fact that any function $ u \in A $ is the difference of two non-negative harmonic functions in $ B _ {n} ( 0 , R ) $. The class of functions representable by a Poisson–Lebesgue integral is a proper subclass of the class $ A $ and contains all bounded harmonic functions in $ B _ {n} ( 0 , R ) $. For almost-all points $ y \in S _ {n} ( 0 , R ) $ with respect to Lebesgue measure on $ S _ {n} ( 0 , R ) $, a Poisson–Stieltjes integral (5) has angular boundary values coinciding with the values of the derivative $ \mu ^ \prime ( y) $ of the measure $ \mu $ with respect to Lebesgue measure. The theory of Poisson–Stieltjes and Poisson–Lebesgue integrals has also been constructed for the half-space (see [5]).
Various modifications of the Poisson integral play a large role in the theory of analytic functions of several complex variables and in its applications to quantum field theory. For example, the Poisson kernel for the polydisc
$$ U ^ {n} = \{ {z = ( z _ {1} \dots z _ {n} ) \in \mathbf C ^ {n} } : { | z _ {j} | < 1 , j = 1 \dots n } \} $$
in the complex space $ \mathbf C ^ {n} $ is obtained by multiplying the kernels (2):
$$ P U ^ {n} ( z , \zeta ) \ = \prod _ { j= } 1 ^ { n } P B _ {2} ( z _ {j} , \zeta _ {j} ) . $$
The corresponding Poisson integral
$$ u ( z) = \int\limits _ {T ^ {n} } f ( \zeta ) P U ^ {n} ( z , \zeta ) d T ^ {n} ( \zeta ) $$
with respect to the distinguished boundary $ T ^ {n} = \{ {\zeta = ( \zeta _ {1} \dots \zeta _ {n} ) \in \mathbf C ^ {n} } : {| \zeta _ {j} | = 1, j = 1 \dots n } \} $ of the polydisc gives a multi-harmonic function $ u ( z) $, $ z \in U ^ {n} $, taking the continuous values $ f ( \zeta ) $ on $ T ^ {n} $. Generalizations in the form of Poisson–Lebesgue and Poisson–Stieltjes integrals are also considered (see [6]).
In quantum field theory Poisson integrals are also applied to tube domains $ T ^ {C} $ in the complex space $ \mathbf C ^ {n} $ over a convex open acute cone $ C $ in the space $ \mathbf R ^ {n} $( with vertex at the origin). These have the form
$$ T ^ {C} = \mathbf R ^ {n} + i C = $$
$$ = \ \{ z = x + i y \in \mathbf C ^ {n} : x = ( x _ {1} \dots x _ {n} ) \in \mathbf R ^ {n} : y = ( y _ {1} \dots y _ {n} ) \in C \} . $$
A Poisson integral of the form (3) for the half-plane when $ n = 2 $ is a particular case of such Poisson integrals for tube domains; the Poisson integral for bounded symmetric domains in the space $ \mathbf C ^ {n} $ is the same as the Poisson integral for a tube domain in the space of matrices. Taking the density of the Poisson integral $ f $ to be a generalized function and the Poisson integral itself to be the convolution of $ f $ with the Poisson kernel one arrives at the important concept of the Poisson integral for certain classes of generalized functions (see [7]–[9]).
References
| [1a] | S.D. Poisson, J. Ecole R. Polytechn. , 11 (1820) pp. 295–341 |
| [1b] | S.D. Poisson, "Suite du mémoire sur les intégrales définies et sur la sommation des séries" J. Ecole R. Polytechn. , 12 (1823) pp. 404–509 |
| [2] | H.A. Schwarz, "Ueber die Integration der partiellen Differentialgleichung 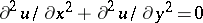 für die Fläche eines Kreises" Vierteljahrsschr. Naturforsch. Ges. Zurich , 15 (1870) pp. 113–128 für die Fläche eines Kreises" Vierteljahrsschr. Naturforsch. Ges. Zurich , 15 (1870) pp. 113–128 |
| [3] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
| [4] | A.N. Tikhonov, A.A. Samarskii, "Equations of mathematical physics" , Pergamon (1963) (Translated from Russian) |
| [5] | E.D. Solomentsev, "Harmonic and subharmonic functions and their generalizations" Itogi Nauk. Mat. Anal. Teor. Veroyatnost. Regulirovanie. 1962 (1964) pp. 83–100 (In Russian) |
| [6] | W. Rudin, "Function theory in polydiscs" , Benjamin (1969) |
| [7] | V.S. Vladimirov, "Generalized functions in mathematical physics" , MIR (1979) (Translated from Russian) |
| [8] | L.K. Hua, "Harmonic analysis of functions of several complex variables in the classical domains" , Amer. Math. Soc. (1963) (Translated from Russian) |
| [9] | E.M. Stein, G. Weiss, "Introduction to Fourier analysis on Euclidean spaces" , Princeton Univ. Press (1971) |
Comments
The Poisson kernel for the exterior of the ball $ B _ {n} ( 0, R) $ is given by
$$ PB _ {n} ^ {c} ( x, y) = \ \frac{1}{\sigma _ {n} } R ^ {n-} 2 \left ( \frac{| x | ^ {2} - R ^ {2} }{| x- y | ^ {n} } + \frac{1}{R ^ {n-} 2 } - \frac{1}{| x | ^ {n-} 2 } \right ) . $$
In case of the unit ball $ B $ in $ \mathbf C ^ {n} $, there are several Poisson-type kernels, e.g. the classical one, solving the classical Dirichlet problem, and the invariant Poisson kernel, which is invariant under holomorphic automorphisms of the unit ball. It reads
$$ P( z, \zeta ) = \frac{( 1- | z | ^ {2} ) }{| 1-\langle z, \zeta \rangle | ^ {2n} } ,\ \ z \in B ,\ \zeta \in \partial B, $$
where $ \langle z, \zeta \rangle = \sum _ {1} ^ {n} z _ {j} \zeta _ {j} $ and $ | z | ^ {2} = \langle z, z \rangle $. This is the analogue for the ball of the Poisson kernel with respect to the distinguished boundary of the polydisc, described above. The invariant Poisson kernel solves the Dirichlet problem for the so-called invariant Laplacian, see [a1].
References
| [a1] | W. Rudin, "Function theory in the unit ball in  " , Springer (1980) " , Springer (1980) |
Poisson integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Poisson_integral&oldid=48219