Difference between revisions of "Operator group"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | A group of operators, a one-parameter group of operators (cf. [[Operator|Operator]]) on a [[Banach space|Banach space]] | + | <!-- |
| + | o0683701.png | ||
| + | $#A+1 = 81 n = 3 | ||
| + | $#C+1 = 81 : ~/encyclopedia/old_files/data/O068/O.0608370 Operator group | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | A group of operators, a one-parameter group of operators (cf. [[Operator|Operator]]) on a [[Banach space|Banach space]] $ E $, | ||
| + | i.e. a family of bounded linear operators $ U _ {t} $, | ||
| + | $ - \infty < t < \infty $, | ||
| + | such that $ U _ {0} = I $, | ||
| + | $ U _ {s+} t = U _ {s} \cdot U _ {t} $ | ||
| + | and $ U _ {t} $ | ||
| + | depends continuously on $ t $( | ||
| + | in the uniform, strong or weak topology). If $ E $ | ||
| + | is a [[Hilbert space|Hilbert space]] and $ \| U _ {t} \| $ | ||
| + | is uniformly bounded, then the group $ \{ U _ {t} \} $ | ||
| + | is similar to a group of unitary operators (Sz.-Nagy's theorem, cf. also [[Unitary operator|Unitary operator]]). | ||
====References==== | ====References==== | ||
| Line 6: | Line 28: | ||
''V.I. Lomonosov'' | ''V.I. Lomonosov'' | ||
| − | A group with operators, a group with domain of operators | + | A group with operators, a group with domain of operators $ \Sigma $, |
| + | where $ \Sigma $ | ||
| + | is a set of symbols, is a [[Group|group]] $ G $ | ||
| + | such that for every element $ a \in G $ | ||
| + | and every $ \sigma \in \Sigma $ | ||
| + | there is a corresponding element $ a \sigma \in G $ | ||
| + | such that $ ( ab) \sigma = a \sigma \cdot b \sigma $ | ||
| + | for any $ a, b \in G $. | ||
| + | Let $ G $ | ||
| + | and $ G ^ \prime $ | ||
| + | be groups with the same domain of operators $ \Sigma $; | ||
| + | an isomorphic (a homomorphic) mapping $ \phi $ | ||
| + | of $ G $ | ||
| + | onto $ G ^ \prime $ | ||
| + | is called an operator isomorphism (operator homomorphism) if $ ( a \sigma ) \phi = ( a \phi ) \sigma $ | ||
| + | for any $ a \in G $, | ||
| + | $ \sigma \in \Sigma $. | ||
| + | A subgroup (normal subgroup) $ H $ | ||
| + | of the group $ G $ | ||
| + | with domain of operators $ \Sigma $ | ||
| + | is called an admissible subgroup (admissible normal subgroup) if $ H \sigma \subseteq H $ | ||
| + | for any $ \sigma \in \Sigma $. | ||
| + | The intersection of all admissible subgroups containing a given subset $ M $ | ||
| + | of $ G $ | ||
| + | is called the admissible subgroup generated by the set $ M $. | ||
| + | A group which does not have admissible normal subgroups apart from itself and the trivial subgroup is called a simple group (with respect to the given domain of operators). Every quotient group of an operator group by an admissible normal subgroup is a group with the same domain of operators. | ||
| − | A group | + | A group $ G $ |
| + | is called a group with a semi-group of operators $ \Sigma $ | ||
| + | if $ G $ | ||
| + | is a group with domain of operators $ \Sigma $, | ||
| + | $ \Sigma $ | ||
| + | is a semi-group and $ a( \sigma \tau ) = ( a \sigma ) \tau $ | ||
| + | for any $ a \in G $, | ||
| + | $ \sigma , \tau \in \Sigma $. | ||
| + | If $ \Sigma $ | ||
| + | is a semi-group with an identity element $ \epsilon $, | ||
| + | it is supposed that $ a \epsilon = a $ | ||
| + | for every $ a \in G $. | ||
| + | Every group with an arbitrary domain of operators $ \Sigma _ {0} $ | ||
| + | is a group with semi-group of operators $ \Sigma $, | ||
| + | where $ \Sigma $ | ||
| + | is the free semi-group generated by the set $ \Sigma _ {0} $. | ||
| + | A group $ F $ | ||
| + | with semi-group of operators $ \Sigma $ | ||
| + | possessing an identity element is called $ \Sigma $- | ||
| + | free if it is generated by a system of elements $ X $ | ||
| + | such that the elements $ x \alpha $, | ||
| + | where $ x \in X $, | ||
| + | $ \alpha \in \Sigma $, | ||
| + | constitute for $ F $( | ||
| + | as a group without operators) a system of free generators. Let $ F $ | ||
| + | be a $ \Gamma $- | ||
| + | free group ( $ \Gamma $ | ||
| + | being a group of operators), let $ \Delta $ | ||
| + | be a subgroup of $ \Gamma $, | ||
| + | let $ f \in F $, | ||
| + | and let $ A _ {f, \Delta } $ | ||
| + | be the admissible subgroup of $ F $ | ||
| + | generated by all elements of the form $ f ^ { - 1 } ( f \alpha ) $, | ||
| + | where $ \alpha \in \Delta $. | ||
| + | Then every admissible subgroup of $ F $ | ||
| + | is an operator free product of groups of type $ A _ {f, \Delta } $ | ||
| + | and a $ \Gamma $- | ||
| + | free group (see [[#References|[2]]]). If $ \Sigma $ | ||
| + | is a free semi-group of operators, then, if $ a \neq 1 $, | ||
| + | the admissible subgroup of the $ \Sigma $- | ||
| + | free group $ F $ | ||
| + | generated by the element $ a $ | ||
| + | is itself a $ \Sigma $- | ||
| + | free group with free generator $ a $( | ||
| + | see also ). | ||
| − | An Abelian group with an associative ring of operators | + | An Abelian group with an associative ring of operators $ K $ |
| + | is just a $ K $- | ||
| + | module (cf. [[Module|Module]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.G. Kurosh, "The theory of groups" , '''1–2''' , Chelsea (1955–1956) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.T. Zavalo, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068370/o06837083.png" />-free operator groups" ''Mat. Sb.'' , '''33''' (1953) pp. 399–432 (In Russian)</TD></TR><TR><TD valign="top">[3a]</TD> <TD valign="top"> S.T. Zavalo, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068370/o06837084.png" />-free operator groups I" ''Ukr. Mat. Zh.'' , '''16''' : 5 (1964) pp. 593–602 (In Russian)</TD></TR><TR><TD valign="top">[3b]</TD> <TD valign="top"> S.T. Zavalo, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068370/o06837085.png" />-free operator groups II" ''Ukr. Mat. Zh.'' , '''16''' : 6 (1964) pp. 730–751 (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.G. Kurosh, "The theory of groups" , '''1–2''' , Chelsea (1955–1956) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.T. Zavalo, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068370/o06837083.png" />-free operator groups" ''Mat. Sb.'' , '''33''' (1953) pp. 399–432 (In Russian)</TD></TR><TR><TD valign="top">[3a]</TD> <TD valign="top"> S.T. Zavalo, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068370/o06837084.png" />-free operator groups I" ''Ukr. Mat. Zh.'' , '''16''' : 5 (1964) pp. 593–602 (In Russian)</TD></TR><TR><TD valign="top">[3b]</TD> <TD valign="top"> S.T. Zavalo, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o068/o068370/o06837085.png" />-free operator groups II" ''Ukr. Mat. Zh.'' , '''16''' : 6 (1964) pp. 730–751 (In Russian)</TD></TR></table> | ||
Latest revision as of 08:04, 6 June 2020
A group of operators, a one-parameter group of operators (cf. Operator) on a Banach space $ E $,
i.e. a family of bounded linear operators $ U _ {t} $,
$ - \infty < t < \infty $,
such that $ U _ {0} = I $,
$ U _ {s+} t = U _ {s} \cdot U _ {t} $
and $ U _ {t} $
depends continuously on $ t $(
in the uniform, strong or weak topology). If $ E $
is a Hilbert space and $ \| U _ {t} \| $
is uniformly bounded, then the group $ \{ U _ {t} \} $
is similar to a group of unitary operators (Sz.-Nagy's theorem, cf. also Unitary operator).
References
| [1] | B. Szökevalfi-Nagy, "On uniformly bounded linear transformations in Hilbert space" Acta Sci. Math. (Szeged) , 11 (1947) pp. 152–157 |
| [2] | E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1948) |
V.I. Lomonosov
A group with operators, a group with domain of operators $ \Sigma $, where $ \Sigma $ is a set of symbols, is a group $ G $ such that for every element $ a \in G $ and every $ \sigma \in \Sigma $ there is a corresponding element $ a \sigma \in G $ such that $ ( ab) \sigma = a \sigma \cdot b \sigma $ for any $ a, b \in G $. Let $ G $ and $ G ^ \prime $ be groups with the same domain of operators $ \Sigma $; an isomorphic (a homomorphic) mapping $ \phi $ of $ G $ onto $ G ^ \prime $ is called an operator isomorphism (operator homomorphism) if $ ( a \sigma ) \phi = ( a \phi ) \sigma $ for any $ a \in G $, $ \sigma \in \Sigma $. A subgroup (normal subgroup) $ H $ of the group $ G $ with domain of operators $ \Sigma $ is called an admissible subgroup (admissible normal subgroup) if $ H \sigma \subseteq H $ for any $ \sigma \in \Sigma $. The intersection of all admissible subgroups containing a given subset $ M $ of $ G $ is called the admissible subgroup generated by the set $ M $. A group which does not have admissible normal subgroups apart from itself and the trivial subgroup is called a simple group (with respect to the given domain of operators). Every quotient group of an operator group by an admissible normal subgroup is a group with the same domain of operators.
A group $ G $ is called a group with a semi-group of operators $ \Sigma $ if $ G $ is a group with domain of operators $ \Sigma $, $ \Sigma $ is a semi-group and $ a( \sigma \tau ) = ( a \sigma ) \tau $ for any $ a \in G $, $ \sigma , \tau \in \Sigma $. If $ \Sigma $ is a semi-group with an identity element $ \epsilon $, it is supposed that $ a \epsilon = a $ for every $ a \in G $. Every group with an arbitrary domain of operators $ \Sigma _ {0} $ is a group with semi-group of operators $ \Sigma $, where $ \Sigma $ is the free semi-group generated by the set $ \Sigma _ {0} $. A group $ F $ with semi-group of operators $ \Sigma $ possessing an identity element is called $ \Sigma $- free if it is generated by a system of elements $ X $ such that the elements $ x \alpha $, where $ x \in X $, $ \alpha \in \Sigma $, constitute for $ F $( as a group without operators) a system of free generators. Let $ F $ be a $ \Gamma $- free group ( $ \Gamma $ being a group of operators), let $ \Delta $ be a subgroup of $ \Gamma $, let $ f \in F $, and let $ A _ {f, \Delta } $ be the admissible subgroup of $ F $ generated by all elements of the form $ f ^ { - 1 } ( f \alpha ) $, where $ \alpha \in \Delta $. Then every admissible subgroup of $ F $ is an operator free product of groups of type $ A _ {f, \Delta } $ and a $ \Gamma $- free group (see [2]). If $ \Sigma $ is a free semi-group of operators, then, if $ a \neq 1 $, the admissible subgroup of the $ \Sigma $- free group $ F $ generated by the element $ a $ is itself a $ \Sigma $- free group with free generator $ a $( see also ).
An Abelian group with an associative ring of operators $ K $ is just a $ K $- module (cf. Module).
References
| [1] | A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian) |
| [2] | S.T. Zavalo, "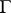 -free operator groups" Mat. Sb. , 33 (1953) pp. 399–432 (In Russian) -free operator groups" Mat. Sb. , 33 (1953) pp. 399–432 (In Russian) |
| [3a] | S.T. Zavalo, "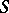 -free operator groups I" Ukr. Mat. Zh. , 16 : 5 (1964) pp. 593–602 (In Russian) -free operator groups I" Ukr. Mat. Zh. , 16 : 5 (1964) pp. 593–602 (In Russian) |
| [3b] | S.T. Zavalo, "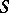 -free operator groups II" Ukr. Mat. Zh. , 16 : 6 (1964) pp. 730–751 (In Russian) -free operator groups II" Ukr. Mat. Zh. , 16 : 6 (1964) pp. 730–751 (In Russian) |
Operator group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Operator_group&oldid=48049