Difference between revisions of "Nuclear-C*-algebra"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | n0678302.png | ||
| + | $#A+1 = 52 n = 2 | ||
| + | $#C+1 = 52 : ~/encyclopedia/old_files/data/N067/N.0607830 Nuclear \BMI C sup \ast\EMI\AAhalgebra | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | A | + | A [[C*-algebra| $ C ^ {*} $- |
| + | algebra]] $ A $ | ||
| + | with the following property: For any $ C ^ {*} $- | ||
| + | algebra $ B $ | ||
| + | there is on the algebraic tensor product $ A \otimes B $ | ||
| + | a unique norm such that the completion of $ A \otimes B $ | ||
| + | with respect to this norm is a $ C ^ {*} $- | ||
| + | algebra. Thus, relative to tensor products, nuclear $ C ^ {*} $- | ||
| + | algebras behave similarly to nuclear spaces (cf. [[Nuclear space|Nuclear space]]) (although infinite-dimensional nuclear $ C ^ {*} $- | ||
| + | algebras are not nuclear spaces). The class of nuclear $ C ^ {*} $- | ||
| + | algebras includes all type I $ C ^ {*} $- | ||
| + | algebras. This class is closed with respect to the inductive limit. If $ I $ | ||
| + | is a closed two-sided ideal in a $ C ^ {*} $- | ||
| + | algebra $ A $, | ||
| + | then $ A $ | ||
| + | is nuclear if and only if $ I $ | ||
| + | and $ A/I $ | ||
| + | are. A subalgebra of a nuclear $ C ^ {*} $- | ||
| + | algebra need not be a nuclear $ C ^ {*} $- | ||
| + | algebra. The tensor product of two $ C ^ {*} $- | ||
| + | algebras $ A $ | ||
| + | and $ B $ | ||
| + | is nuclear if and only if $ A $ | ||
| + | and $ B $( | ||
| + | both) are nuclear. If $ G $ | ||
| + | is an amenable locally compact group, then the enveloping $ C ^ {*} $- | ||
| + | algebra of the group algebra $ L _ {1} ( G) $ | ||
| + | is nuclear (the converse is not true). Each [[Factor representation|factor representation]] of a nuclear $ C ^ {*} $- | ||
| + | algebra is hyperfinite, that is, the [[Von Neumann algebra|von Neumann algebra]] generated by this representation can be obtained from an increasing sequence of finite-dimensional factors (matrix algebras). Any factor state on a nuclear $ C ^ {*} $- | ||
| + | subalgebra of a $ C ^ {*} $- | ||
| + | algebra can be extended to a factor state on the whole algebra. | ||
| − | + | Let $ L ( H) $ | |
| + | be the $ C ^ {*} $- | ||
| + | algebra of all bounded linear operators on a Hilbert space $ H $, | ||
| + | and let $ A $ | ||
| + | be a $ C ^ {*} $- | ||
| + | algebra of operators on $ H $. | ||
| + | If $ A $ | ||
| + | is nuclear, then its weak closure $ \overline{A}\; $ | ||
| + | is an injective von Neumann algebra, that is, there is a projection $ L ( H) \rightarrow \overline{A}\; $ | ||
| + | with norm one; in this case the commutant $ A ^ \prime $ | ||
| + | of $ A $ | ||
| + | is also injective. An arbitrary $ C ^ {*} $- | ||
| + | algebra $ A $ | ||
| + | is nuclear if and only if its enveloping von Neumann algebra is injective. | ||
| + | |||
| + | A $ C ^ {*} $- | ||
| + | algebra $ A $ | ||
| + | is nuclear if and only if it has the completely positive approximation property, i.e. the identity operator in $ A $ | ||
| + | can be approximated in the strong operator topology by linear operators of finite rank with norm not exceeding 1, and with the additional property of "complete positivity" [[#References|[1]]]. | ||
| + | |||
| + | Every nuclear $ C ^ {*} $- | ||
| + | algebra has the approximation and bounded approximation properties (see [[Nuclear operator|Nuclear operator]]). There is, however, a non-nuclear $ C ^ {*} $- | ||
| + | algebra with the bounded approximation property. The $ C ^ {*} $- | ||
| + | algebra $ L ( H) $ | ||
| + | of all bounded operators on an infinite-dimensional Hilbert space $ H $ | ||
| + | does not have the completely positive approximation property, or even the approximation property, so that $ L ( H) $ | ||
| + | is not nuclear. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> E.C. Lance, "Tensor products and nuclear <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067830/n06783056.png" />-algebras" R.V. Kadison (ed.) , ''Operator algebras and applications'' , ''Proc. Symp. Pure Math.'' , '''38''' , Amer. Math. Soc. (1982) pp. 379–399</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> O. Bratteli, D.W. Robinson, "Operator algebras and quantum statistical mechanics" , '''1''' , Springer (1979)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E.C. Lance, "Tensor products and nuclear <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067830/n06783056.png" />-algebras" R.V. Kadison (ed.) , ''Operator algebras and applications'' , ''Proc. Symp. Pure Math.'' , '''38''' , Amer. Math. Soc. (1982) pp. 379–399</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> O. Bratteli, D.W. Robinson, "Operator algebras and quantum statistical mechanics" , '''1''' , Springer (1979)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.V. Kadison, J.R. Ringrose, "Fundamentals of the theory of operator algebras" , '''1–2''' , Acad. Press (1983)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> G.K. Pedersen, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067830/n06783057.png" />-algebras and their automorphism groups" , Acad. Press (1979) pp. Sect. 8.15.15</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.V. Kadison, J.R. Ringrose, "Fundamentals of the theory of operator algebras" , '''1–2''' , Acad. Press (1983)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> G.K. Pedersen, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067830/n06783057.png" />-algebras and their automorphism groups" , Acad. Press (1979) pp. Sect. 8.15.15</TD></TR></table> | ||
Revision as of 08:03, 6 June 2020
A $ C ^ {*} $-
algebra $ A $
with the following property: For any $ C ^ {*} $-
algebra $ B $
there is on the algebraic tensor product $ A \otimes B $
a unique norm such that the completion of $ A \otimes B $
with respect to this norm is a $ C ^ {*} $-
algebra. Thus, relative to tensor products, nuclear $ C ^ {*} $-
algebras behave similarly to nuclear spaces (cf. Nuclear space) (although infinite-dimensional nuclear $ C ^ {*} $-
algebras are not nuclear spaces). The class of nuclear $ C ^ {*} $-
algebras includes all type I $ C ^ {*} $-
algebras. This class is closed with respect to the inductive limit. If $ I $
is a closed two-sided ideal in a $ C ^ {*} $-
algebra $ A $,
then $ A $
is nuclear if and only if $ I $
and $ A/I $
are. A subalgebra of a nuclear $ C ^ {*} $-
algebra need not be a nuclear $ C ^ {*} $-
algebra. The tensor product of two $ C ^ {*} $-
algebras $ A $
and $ B $
is nuclear if and only if $ A $
and $ B $(
both) are nuclear. If $ G $
is an amenable locally compact group, then the enveloping $ C ^ {*} $-
algebra of the group algebra $ L _ {1} ( G) $
is nuclear (the converse is not true). Each factor representation of a nuclear $ C ^ {*} $-
algebra is hyperfinite, that is, the von Neumann algebra generated by this representation can be obtained from an increasing sequence of finite-dimensional factors (matrix algebras). Any factor state on a nuclear $ C ^ {*} $-
subalgebra of a $ C ^ {*} $-
algebra can be extended to a factor state on the whole algebra.
Let $ L ( H) $ be the $ C ^ {*} $- algebra of all bounded linear operators on a Hilbert space $ H $, and let $ A $ be a $ C ^ {*} $- algebra of operators on $ H $. If $ A $ is nuclear, then its weak closure $ \overline{A}\; $ is an injective von Neumann algebra, that is, there is a projection $ L ( H) \rightarrow \overline{A}\; $ with norm one; in this case the commutant $ A ^ \prime $ of $ A $ is also injective. An arbitrary $ C ^ {*} $- algebra $ A $ is nuclear if and only if its enveloping von Neumann algebra is injective.
A $ C ^ {*} $- algebra $ A $ is nuclear if and only if it has the completely positive approximation property, i.e. the identity operator in $ A $ can be approximated in the strong operator topology by linear operators of finite rank with norm not exceeding 1, and with the additional property of "complete positivity" [1].
Every nuclear $ C ^ {*} $- algebra has the approximation and bounded approximation properties (see Nuclear operator). There is, however, a non-nuclear $ C ^ {*} $- algebra with the bounded approximation property. The $ C ^ {*} $- algebra $ L ( H) $ of all bounded operators on an infinite-dimensional Hilbert space $ H $ does not have the completely positive approximation property, or even the approximation property, so that $ L ( H) $ is not nuclear.
References
| [1] | E.C. Lance, "Tensor products and nuclear 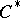 -algebras" R.V. Kadison (ed.) , Operator algebras and applications , Proc. Symp. Pure Math. , 38 , Amer. Math. Soc. (1982) pp. 379–399 -algebras" R.V. Kadison (ed.) , Operator algebras and applications , Proc. Symp. Pure Math. , 38 , Amer. Math. Soc. (1982) pp. 379–399 |
| [2] | O. Bratteli, D.W. Robinson, "Operator algebras and quantum statistical mechanics" , 1 , Springer (1979) |
Comments
References
| [a1] | R.V. Kadison, J.R. Ringrose, "Fundamentals of the theory of operator algebras" , 1–2 , Acad. Press (1983) |
| [a2] | G.K. Pedersen, "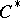 -algebras and their automorphism groups" , Acad. Press (1979) pp. Sect. 8.15.15 -algebras and their automorphism groups" , Acad. Press (1979) pp. Sect. 8.15.15 |
Nuclear-C*-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nuclear-C*-algebra&oldid=48023