Difference between revisions of "Newton diagram"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | n0665201.png | ||
| + | $#A+1 = 75 n = 0 | ||
| + | $#C+1 = 75 : ~/encyclopedia/old_files/data/N066/N.0606520 Newton diagram, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''Newton polygon'' | ''Newton polygon'' | ||
A convex polygonal line, introduced by I. Newton in 1669 (see [[#References|[1]]]) to determine the exponents of the principal terms of algebraic functions. The process of finding successively the terms of the expansion of an algebraic function with the help of the Newton diagram is called the method of the Newton diagram. In more detail it was worked out by V. Puiseux [[#References|[2]]] and it is sometimes called the Puiseux diagram in mathematical literature. Before Puiseux, an algebraic version of the Newton diagram was studied by J.L. Lagrange [[#References|[3]]]. | A convex polygonal line, introduced by I. Newton in 1669 (see [[#References|[1]]]) to determine the exponents of the principal terms of algebraic functions. The process of finding successively the terms of the expansion of an algebraic function with the help of the Newton diagram is called the method of the Newton diagram. In more detail it was worked out by V. Puiseux [[#References|[2]]] and it is sometimes called the Puiseux diagram in mathematical literature. Before Puiseux, an algebraic version of the Newton diagram was studied by J.L. Lagrange [[#References|[3]]]. | ||
| − | Let | + | Let $ F ( x, y) $ |
| + | be a pseudo-polynomial in $ y $, | ||
| + | that is, let | ||
| − | + | $$ | |
| + | F ( x, y) = \ | ||
| + | \sum _ {s = 0 } ^ { n } | ||
| + | F _ {s} ( x) y ^ {s} , | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | F _ {s} ( x) = \ | ||
| + | x ^ {\rho _ {s} } | ||
| + | \sum _ {r = 0 } ^ \infty | ||
| + | F _ {rs} x ^ {r/p} , | ||
| + | $$ | ||
| − | + | $ x $ | |
| + | and $ y $ | ||
| + | are complex variables, $ F _ {rs} $ | ||
| + | are complex numbers, $ p $ | ||
| + | is a natural number, $ \rho _ {s} $ | ||
| + | are non-negative rational numbers, $ F _ {n} ( x) \not\equiv 0 $, | ||
| + | and $ F _ {0} ( x) \not\equiv 0 $. | ||
| + | As a rule one assumes that if $ F _ {s} ( x) \not\equiv 0 $, | ||
| + | then $ F _ {0s} ( x) \not\equiv 0 $, | ||
| + | hence, $ F _ {00} \neq 0 $, | ||
| + | $ F _ {0n} \neq 0 $. | ||
| + | A solution $ y = y ( \lambda ) $ | ||
| + | of the equation | ||
| − | + | $$ \tag{1 } | |
| + | F ( x, y) = 0 | ||
| + | $$ | ||
is sought for in the form of a series | is sought for in the form of a series | ||
| − | + | $$ \tag{2 } | |
| + | y = y _ \epsilon x ^ \epsilon + | ||
| + | y _ {\epsilon ^ \prime } x ^ {\epsilon ^ \prime } + \dots , | ||
| + | $$ | ||
| − | where < | + | where $ \epsilon < \epsilon ^ \prime < \dots $ |
| + | or, briefly, $ y = y _ \epsilon x ^ \epsilon + z $, | ||
| + | $ z = o ( x ^ \epsilon ) $ | ||
| + | as $ x \rightarrow 0 $. | ||
| + | To determine the possible values of $ \epsilon $ | ||
| + | and $ y _ \epsilon $ | ||
| + | one substitutes (2) in (1), collects terms with equal powers of $ x $, | ||
| + | and equates to zero the coefficients of these powers. | ||
| − | The process begins with the term of lowest degree. As long as the exponent | + | The process begins with the term of lowest degree. As long as the exponent $ \epsilon $ |
| + | is not yet determined, there is no way of telling which of the resulting terms are lowest in $ x $. | ||
| + | However, the terms of lowest order are among the following: | ||
| − | + | $$ \tag{3 } | |
| + | F _ {00} x ^ {\rho _ {0} } ,\ \ | ||
| + | F _ {0k} y _ {\epsilon ^ {k} } | ||
| + | x ^ {\rho _ {k} + k \epsilon } ,\ \ | ||
| + | F _ {0n} y _ \epsilon ^ {n} x ^ {\rho _ {n} + n \epsilon } , | ||
| + | $$ | ||
| − | where | + | where $ k $ |
| + | ranges over those values $ 1, 2 \dots $ | ||
| + | for which $ F _ {k} ( x) \not\equiv 0 $. | ||
| + | To annihilate the terms of lowest order one has to choose $ \epsilon $ | ||
| + | so that at least two of the exponents $ \rho _ {0} $, | ||
| + | $ \rho _ {k} + k \epsilon $, | ||
| + | $ \rho _ {n} + n \epsilon $ | ||
| + | coincide and the remaining ones are to be not smaller. This argument leads to Newton's diagram. | ||
| − | In the plane one takes a rectangular Cartesian coordinate system and plots the points | + | In the plane one takes a rectangular Cartesian coordinate system and plots the points $ ( 0, \rho _ {0} ) $, |
| + | $ ( k, \rho _ {k} ) $ | ||
| + | and $ ( n, \rho _ {n} ) $, | ||
| + | where $ k $ | ||
| + | ranges over the same values as in (3). Through the point $ ( 0, \rho _ {0} ) $ | ||
| + | one draws the line that coincides with the $ y $- | ||
| + | axis and then rotates around $ ( 0, \rho _ {0} ) $ | ||
| + | anti-clockwise until it falls onto one of the plotted points, say $ ( l, \rho _ {l} ) $. | ||
| + | The tangent of the angle that the line $ L $ | ||
| + | passing through $ ( 0, \rho _ {0} ) $ | ||
| + | and $ ( l, \rho _ {l} ) $ | ||
| + | makes with the negative $ x $- | ||
| + | axis is one of the values $ \epsilon $, | ||
| + | since $ \rho _ {0} = \rho _ {l} + l _ \epsilon $, | ||
| + | and $ \rho _ {k} + k \epsilon > \rho _ {l} + l _ \epsilon $ | ||
| + | if $ ( k, \rho _ {k} ) \notin L $. | ||
| + | Suppose that $ ( s, \rho _ {s} ) $ | ||
| + | is the point on $ L $ | ||
| + | with largest $ x $- | ||
| + | coordinate and that $ L $ | ||
| + | is rotated anti-clockwise around $ ( s, \rho _ {s} ) $ | ||
| + | until it falls onto another one of the plotted points, say, $ ( t, \rho _ {t} ) $ | ||
| + | with $ t > s $. | ||
| + | Let $ L ^ \prime $ | ||
| + | be the line through $ ( s, \rho _ {s} ) $ | ||
| + | and $ ( t, \rho _ {t} ) $. | ||
| + | The tangent of the angle between $ L ^ \prime $ | ||
| + | and the negative $ x $- | ||
| + | axis gives another possible value of $ \epsilon $. | ||
| + | Continuing these constructions one obtains a convex polygonal line, which is called Newton's diagram. | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/n066520a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/n066520a.gif" /> | ||
| Line 33: | Line 123: | ||
Figure: n066520a | Figure: n066520a | ||
| − | The value of the coefficient of | + | The value of the coefficient of $ y _ {s} ^ \epsilon $ |
| + | is determined as follows. Let $ ( i, \rho _ {i} ) $ | ||
| + | and $ ( j, \rho _ {j} ) $ | ||
| + | be the extreme points of a segment of the Newton diagram that determines one of the possible values of $ \epsilon $. | ||
| + | To annihilate the terms of lowest order when (2) is substituted in (1) it is necessary and sufficient that | ||
| − | + | $$ \tag{4 } | |
| + | {\sum _ \epsilon } {} \prime | ||
| + | F _ {0s} y _ \epsilon ^ {s} = 0, | ||
| + | $$ | ||
| − | where the prime in the sum denotes that summation is over those | + | where the prime in the sum denotes that summation is over those $ \rho $ |
| + | for which $ \rho _ {s} + s \epsilon = \rho _ {i} + i \epsilon $. | ||
| + | Equation (4) has $ j - i $ | ||
| + | non-zero roots (including multiplicity), that is, as many as the length of the projection of the relevant segment of the Newton diagram. Hence it is clear that by the method of the Newton diagram one obtains all $ n $ | ||
| + | values of the principal term $ y _ \epsilon x ^ \epsilon $ | ||
| + | in (2). By the same method one determines the next term in the expansion (2), etc. As a result, all $ n $ | ||
| + | solutions of (1) have the form (2), so-called Puiseux series (see [[Algebraic function|Algebraic function]]). The method of the Newton diagram is also applicable to the solution of differential equations. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> I. Newton, "The mathematical papers of I. Newton" , '''1–8''' , Cambridge Univ. Press (1967–1981)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V. Puiseux, "Récherches sur les fonctions algébriques" ''J. Math. Pure Appl.'' , '''15''' (1850) pp. 365–480</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J.L. Lagrange, "Solution de quelques problèmes d'astronomie sphérique par le moyen des séries" ''Nouv. Mém. Acad. Roy. Sci. Belles Lettres Berlin'' (1776)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.M. Vainberg, V.A. Trenogin, "Theory of branching of solutions of non-linear equations" , Noordhoff (1974) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> , ''Isaac Newton 1643 - 1727; a collection of articles on the tercentenary of his birth'' , Moscow (1943) (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> A.D. [A.D. Bryuno] Bruno, "Local methods in nonlinear differential equations" , Springer (1989) (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I. Newton, "The mathematical papers of I. Newton" , '''1–8''' , Cambridge Univ. Press (1967–1981)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V. Puiseux, "Récherches sur les fonctions algébriques" ''J. Math. Pure Appl.'' , '''15''' (1850) pp. 365–480</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J.L. Lagrange, "Solution de quelques problèmes d'astronomie sphérique par le moyen des séries" ''Nouv. Mém. Acad. Roy. Sci. Belles Lettres Berlin'' (1776)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.M. Vainberg, V.A. Trenogin, "Theory of branching of solutions of non-linear equations" , Noordhoff (1974) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> , ''Isaac Newton 1643 - 1727; a collection of articles on the tercentenary of his birth'' , Moscow (1943) (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> A.D. [A.D. Bryuno] Bruno, "Local methods in nonlinear differential equations" , Springer (1989) (Translated from Russian)</TD></TR></table> | ||
Latest revision as of 08:02, 6 June 2020
Newton polygon
A convex polygonal line, introduced by I. Newton in 1669 (see [1]) to determine the exponents of the principal terms of algebraic functions. The process of finding successively the terms of the expansion of an algebraic function with the help of the Newton diagram is called the method of the Newton diagram. In more detail it was worked out by V. Puiseux [2] and it is sometimes called the Puiseux diagram in mathematical literature. Before Puiseux, an algebraic version of the Newton diagram was studied by J.L. Lagrange [3].
Let $ F ( x, y) $ be a pseudo-polynomial in $ y $, that is, let
$$ F ( x, y) = \ \sum _ {s = 0 } ^ { n } F _ {s} ( x) y ^ {s} , $$
where
$$ F _ {s} ( x) = \ x ^ {\rho _ {s} } \sum _ {r = 0 } ^ \infty F _ {rs} x ^ {r/p} , $$
$ x $ and $ y $ are complex variables, $ F _ {rs} $ are complex numbers, $ p $ is a natural number, $ \rho _ {s} $ are non-negative rational numbers, $ F _ {n} ( x) \not\equiv 0 $, and $ F _ {0} ( x) \not\equiv 0 $. As a rule one assumes that if $ F _ {s} ( x) \not\equiv 0 $, then $ F _ {0s} ( x) \not\equiv 0 $, hence, $ F _ {00} \neq 0 $, $ F _ {0n} \neq 0 $. A solution $ y = y ( \lambda ) $ of the equation
$$ \tag{1 } F ( x, y) = 0 $$
is sought for in the form of a series
$$ \tag{2 } y = y _ \epsilon x ^ \epsilon + y _ {\epsilon ^ \prime } x ^ {\epsilon ^ \prime } + \dots , $$
where $ \epsilon < \epsilon ^ \prime < \dots $ or, briefly, $ y = y _ \epsilon x ^ \epsilon + z $, $ z = o ( x ^ \epsilon ) $ as $ x \rightarrow 0 $. To determine the possible values of $ \epsilon $ and $ y _ \epsilon $ one substitutes (2) in (1), collects terms with equal powers of $ x $, and equates to zero the coefficients of these powers.
The process begins with the term of lowest degree. As long as the exponent $ \epsilon $ is not yet determined, there is no way of telling which of the resulting terms are lowest in $ x $. However, the terms of lowest order are among the following:
$$ \tag{3 } F _ {00} x ^ {\rho _ {0} } ,\ \ F _ {0k} y _ {\epsilon ^ {k} } x ^ {\rho _ {k} + k \epsilon } ,\ \ F _ {0n} y _ \epsilon ^ {n} x ^ {\rho _ {n} + n \epsilon } , $$
where $ k $ ranges over those values $ 1, 2 \dots $ for which $ F _ {k} ( x) \not\equiv 0 $. To annihilate the terms of lowest order one has to choose $ \epsilon $ so that at least two of the exponents $ \rho _ {0} $, $ \rho _ {k} + k \epsilon $, $ \rho _ {n} + n \epsilon $ coincide and the remaining ones are to be not smaller. This argument leads to Newton's diagram.
In the plane one takes a rectangular Cartesian coordinate system and plots the points $ ( 0, \rho _ {0} ) $, $ ( k, \rho _ {k} ) $ and $ ( n, \rho _ {n} ) $, where $ k $ ranges over the same values as in (3). Through the point $ ( 0, \rho _ {0} ) $ one draws the line that coincides with the $ y $- axis and then rotates around $ ( 0, \rho _ {0} ) $ anti-clockwise until it falls onto one of the plotted points, say $ ( l, \rho _ {l} ) $. The tangent of the angle that the line $ L $ passing through $ ( 0, \rho _ {0} ) $ and $ ( l, \rho _ {l} ) $ makes with the negative $ x $- axis is one of the values $ \epsilon $, since $ \rho _ {0} = \rho _ {l} + l _ \epsilon $, and $ \rho _ {k} + k \epsilon > \rho _ {l} + l _ \epsilon $ if $ ( k, \rho _ {k} ) \notin L $. Suppose that $ ( s, \rho _ {s} ) $ is the point on $ L $ with largest $ x $- coordinate and that $ L $ is rotated anti-clockwise around $ ( s, \rho _ {s} ) $ until it falls onto another one of the plotted points, say, $ ( t, \rho _ {t} ) $ with $ t > s $. Let $ L ^ \prime $ be the line through $ ( s, \rho _ {s} ) $ and $ ( t, \rho _ {t} ) $. The tangent of the angle between $ L ^ \prime $ and the negative $ x $- axis gives another possible value of $ \epsilon $. Continuing these constructions one obtains a convex polygonal line, which is called Newton's diagram.
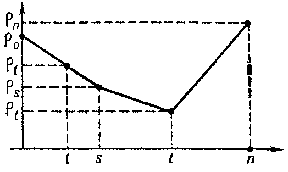
Figure: n066520a
The value of the coefficient of $ y _ {s} ^ \epsilon $ is determined as follows. Let $ ( i, \rho _ {i} ) $ and $ ( j, \rho _ {j} ) $ be the extreme points of a segment of the Newton diagram that determines one of the possible values of $ \epsilon $. To annihilate the terms of lowest order when (2) is substituted in (1) it is necessary and sufficient that
$$ \tag{4 } {\sum _ \epsilon } {} \prime F _ {0s} y _ \epsilon ^ {s} = 0, $$
where the prime in the sum denotes that summation is over those $ \rho $ for which $ \rho _ {s} + s \epsilon = \rho _ {i} + i \epsilon $. Equation (4) has $ j - i $ non-zero roots (including multiplicity), that is, as many as the length of the projection of the relevant segment of the Newton diagram. Hence it is clear that by the method of the Newton diagram one obtains all $ n $ values of the principal term $ y _ \epsilon x ^ \epsilon $ in (2). By the same method one determines the next term in the expansion (2), etc. As a result, all $ n $ solutions of (1) have the form (2), so-called Puiseux series (see Algebraic function). The method of the Newton diagram is also applicable to the solution of differential equations.
References
| [1] | I. Newton, "The mathematical papers of I. Newton" , 1–8 , Cambridge Univ. Press (1967–1981) |
| [2] | V. Puiseux, "Récherches sur les fonctions algébriques" J. Math. Pure Appl. , 15 (1850) pp. 365–480 |
| [3] | J.L. Lagrange, "Solution de quelques problèmes d'astronomie sphérique par le moyen des séries" Nouv. Mém. Acad. Roy. Sci. Belles Lettres Berlin (1776) |
| [4] | M.M. Vainberg, V.A. Trenogin, "Theory of branching of solutions of non-linear equations" , Noordhoff (1974) (Translated from Russian) |
| [5] | , Isaac Newton 1643 - 1727; a collection of articles on the tercentenary of his birth , Moscow (1943) (In Russian) |
| [6] | A.D. [A.D. Bryuno] Bruno, "Local methods in nonlinear differential equations" , Springer (1989) (Translated from Russian) |
Newton diagram. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Newton_diagram&oldid=47966