Difference between revisions of "Martin boundary in the theory of Markov processes"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | m0625601.png | ||
| + | $#A+1 = 87 n = 1 | ||
| + | $#C+1 = 87 : ~/encyclopedia/old_files/data/M062/M.0602560 Martin boundary in the theory of Markov processes | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
The boundary of the state space of a [[Markov process|Markov process]] or of its image in some compact space, constructed by a scheme similar to the Martin scheme (see [[#References|[1]]]). | The boundary of the state space of a [[Markov process|Markov process]] or of its image in some compact space, constructed by a scheme similar to the Martin scheme (see [[#References|[1]]]). | ||
A probabilistic interpretation of Martin's construction was first proposed by J.L. Doob (see [[#References|[4]]]), who discussed the case of discrete Markov chains. | A probabilistic interpretation of Martin's construction was first proposed by J.L. Doob (see [[#References|[4]]]), who discussed the case of discrete Markov chains. | ||
| − | Let | + | Let $ P ( t , x , B ) $ |
| + | be the [[Transition function|transition function]] of a homogeneous Markov process $ X = ( x _ {t} , \zeta , F _ {t} , {\mathsf P} _ {x} ) $, | ||
| + | given on a separable, locally compact space $ E $, | ||
| + | where $ t \geq 0 $, | ||
| + | $ x \in E $, | ||
| + | $ B \in {\mathcal B} $, | ||
| + | and $ {\mathcal B} $ | ||
| + | is the family of Borel sets in $ E $. | ||
| + | A function $ g _ \alpha ( x , y ) \geq 0 $ | ||
| + | defined for $ \alpha \geq 0 $, | ||
| + | $ x \in E $, | ||
| + | $ y \in E $, | ||
| + | which is $ ( {\mathcal B} \times {\mathcal B} ) $- | ||
| + | measurable for fixed $ \alpha $ | ||
| + | is called a Green's function if for each $ B \in {\mathcal B} $, | ||
| − | + | $$ | |
| + | \int\limits _ { B } g _ \alpha ( x , y ) m ( d y ) \equiv \ | ||
| + | \int\limits _ { 0 } ^ \infty e ^ {- \alpha t } P ( t , x , B ) d t , | ||
| + | $$ | ||
| − | where | + | where $ m $ |
| + | is a measure on $ {\mathcal B} $. | ||
| + | To avoid ambiguity in the definition of a Green's function, it can be required in addition that for any continuous function $ f ( x) $ | ||
| + | with compact support, the function | ||
| − | + | $$ | |
| + | g _ \alpha ( \cdot ) = \ | ||
| + | \int\limits _ { E } f ( x) | ||
| + | g _ \alpha ( x , \cdot ) | ||
| + | m ( d x ) | ||
| + | $$ | ||
| − | is | + | is $ \Lambda $- |
| + | continuous (meaning that there exists a function $ F ( t , \omega ) $ | ||
| + | which is left continuous in $ t $ | ||
| + | and such that | ||
| − | + | $$ | |
| + | {\mathsf P} _ {x} \{ F ( t , \omega ) \neq | ||
| + | g _ \alpha ( x _ {t} ( \omega ) ) \} \equiv 0 ,\ \ | ||
| + | x \in E ,\ t > 0 \textrm{ ) } . | ||
| + | $$ | ||
| − | Fixing a measure | + | Fixing a measure $ \gamma $ |
| + | in $ {\mathcal B} $ | ||
| + | and postulating the existence of a Green's function, one defines the Martin kernel | ||
| − | + | $$ | |
| + | K _ {y} ^ \alpha ( x) = \ | ||
| + | |||
| + | \frac{g _ \alpha ( x , y ) }{q ( y ) } | ||
| + | , | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | q ( y) = \int\limits _ { E } | ||
| + | g _ \alpha ( x , y ) | ||
| + | \gamma ( d x ) | ||
| + | $$ | ||
| − | (here some restrictions must be introduced to ensure, in particular, the positivity and | + | (here some restrictions must be introduced to ensure, in particular, the positivity and $ \Lambda $- |
| + | continuity of $ q ( y) $). | ||
| + | If $ \gamma $ | ||
| + | is the unit measure concentrated at some point and $ X $ | ||
| + | is a [[Wiener process|Wiener process]] terminating at the first exit time for some domain, then the definition of $ K _ {y} ^ {0} ( x) $ | ||
| + | reduces to an analogous form [[#References|[1]]]. Under broad conditions one can establish the existence of a compact set $ {\mathcal E} $( | ||
| + | the "Martin compactum" ), a measure $ K _ {y} ^ \alpha ( d x ) $ | ||
| + | on $ {\mathcal B} $( | ||
| + | $ \alpha \geq 0 $, | ||
| + | $ y \in {\mathcal E} $) | ||
| + | and a mapping $ i : E \rightarrow {\mathcal E} $ | ||
| + | for which: a) $ i ( E) $ | ||
| + | is dense in $ {\mathcal E} $; | ||
| + | b) the function | ||
| − | + | $$ | |
| + | K _ {y} ^ \alpha ( f ) = \ | ||
| + | \int\limits _ {\mathcal B} f ( x) K _ {y} ^ \alpha ( d x ) | ||
| + | $$ | ||
| − | separates points and is continuous on | + | separates points and is continuous on $ {\mathcal E} $ |
| + | as $ f $ | ||
| + | runs through all continuous function in $ E $ | ||
| + | with compact support; and c) the measure $ K _ {i ( y) } ^ \alpha ( d x ) $ | ||
| + | coincides with $ K _ {y} ^ \alpha ( x) m ( d x ) $ | ||
| + | if $ y \in E $. | ||
| + | The boundary of the set $ i ( E) $ | ||
| + | in $ {\mathcal E} $ | ||
| + | is called the Martin boundary or exit-boundary (in the study of decompositions of excessive measures the dual object, the entrance-boundary, arises; see [[#References|[3]]], [[#References|[4]]]). | ||
| − | In order to describe the properties of | + | In order to describe the properties of $ {\mathcal E} $ |
| + | it is convenient to invoke $ h $- | ||
| + | processes in the sense of Doob: to each [[Excessive function|excessive function]] $ h $ | ||
| + | is associated the transition function | ||
| − | + | $$ | |
| + | P ^ {h} ( t , x , B ) = \ | ||
| + | h ^ {-} 1 ( x) \int\limits _ { E } | ||
| + | h ( y) P ( t , x , d y ) | ||
| + | $$ | ||
| − | on | + | on $ ( E ^ {h} , {\mathcal B} ^ {h} ) $, |
| + | where $ E ^ {h} = \{ {x \in E } : {0 < h ( x) < \infty } \} $ | ||
| + | and $ {\mathcal B} ^ {h} = \{ {A \in B } : {A \subset E ^ {h} } \} $; | ||
| + | the corresponding Markov process is an $ h $- | ||
| + | process. All $ h $- | ||
| + | processes can be realized, together with $ X $, | ||
| + | on the space of elementary events, so that they are distinguished only by the families of measures $ \{ {\mathsf P} _ {x} ^ {h} \} $. | ||
| + | One constructs in $ {\mathcal E} $ | ||
| + | a modification of $ x _ {t} $, | ||
| + | a left-continuous process $ z _ {t} $( | ||
| + | $ 0 < t \leq \zeta $) | ||
| + | for which $ {\mathsf P} _ {x} ^ {h} \{ z _ {t} \neq i ( x _ {t} ) \} \equiv 0 $ | ||
| + | if $ h \in L _ {1} ( \gamma ) $. | ||
| + | In the topology of $ {\mathcal E} $ | ||
| + | the limit $ z _ \zeta = \lim\limits _ {t \uparrow \zeta } z _ {t} $ | ||
| + | exists almost certainly. | ||
| − | There is a set | + | There is a set $ U \subset {\mathcal E} $( |
| + | the "exit space" ) such that: first, $ {\mathsf P} _ {x} ^ {h} \{ z _ \zeta \in U \} \equiv 1 $ | ||
| + | for all $ h ( x) $ | ||
| + | of the above form; secondly, the measure $ K _ {y} ^ \alpha $ | ||
| + | for $ y \in U $ | ||
| + | has a density $ k _ {y} ^ \alpha ( \cdot ) $ | ||
| + | with respect to $ m $, | ||
| + | where one can take for $ k _ {y} ^ {0} ( \cdot ) $ | ||
| + | an excessive function whose spectral measure is the unit measure concentrated at $ y $; | ||
| + | and thirdly, $ h ( x) $ | ||
| + | admits a unique integral decomposition of the form | ||
| − | + | $$ | |
| + | h ( x) = \int\limits _ { U } k _ {y} ^ {0} ( x) \mu ( d x ) . | ||
| + | $$ | ||
| − | The measure | + | The measure $ \mu $ |
| + | in the decomposition is called the spectral measure of the function $ h $; | ||
| + | it is given by the formula | ||
| − | + | $$ | |
| + | \mu ( B) = \int\limits _ { E } | ||
| + | h ( x) {\mathsf P} _ {x} ^ {h} | ||
| + | \{ z _ \zeta \in B \} | ||
| + | \gamma ( d x ) , | ||
| + | $$ | ||
| − | where | + | where $ B $ |
| + | is a Borel set in $ {\mathcal E} $. | ||
In the theory of Markov processes other types of compactifications are also used, particularly those in which any function of the form | In the theory of Markov processes other types of compactifications are also used, particularly those in which any function of the form | ||
| − | + | $$ | |
| + | \int\limits _ { 0 } ^ \infty | ||
| + | e ^ {- \alpha t } \ | ||
| + | d t \int\limits _ { E } | ||
| + | f ( y) P ( t , x , d y ) ,\ \ | ||
| + | \alpha > 0 ,\ x \in E , | ||
| + | $$ | ||
| − | has a continuous extension for a sufficiently general set of functions | + | has a continuous extension for a sufficiently general set of functions $ f $. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> R.S. Martin, "Minimal positive harmonic functions" ''Trans. Amer. Math. Soc.'' , '''49''' (1941) pp. 137–172</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M. Motoo, "Application of additive functionals to the boundary problem of Markov processes. Lévy's system of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062560/m06256090.png" />-processes" , ''Proc. 5-th Berkeley Symp. Math. Stat. Probab.'' , '''2''' : 2 (1967) pp. 75–110</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H. Kunita, T. Watanabe, "Some theorems concerning resolvents over locally compact spaces" , ''Proc. 5-th Berkeley Symp. Math. Stat. Probab.'' , '''2''' : 2 (1967) pp. 131–164</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J.L. Doob, "Discrete potential theory and boundaries" ''J. Math. and Mech.'' , '''8''' : 3 (1959) pp. 433–458; 993</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> T. Watanabe, "On the theory of Martin boundaries induced by countable Markov processes" ''Mem. Coll. Sci. Kyoto Univ. Ser. A'' , '''33''' : 1 (1960) pp. 39–108</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> G.A. Hunt, "Markov chains and Markov boundaries" ''Illinois J. Math.'' , '''4''' (1960) pp. 313–340</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> P.L. Hennequin, A. Tortrat, "Théorie des probabilites et quelques applications" , Masson (1965)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> H. Kunita, T. Watanabe, "Markov processes and Martin boundaries I" ''Illinois J. Math.'' , '''9''' : 3 (1965) pp. 485–526</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> M.G. Shur, ''Trudy Moskov. Inst. Elektron. Mashinostr.'' , '''5''' (1970) pp. 192–251</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> T. Jeulin, "Compactification de Martin d'un processus droit" ''Z. Wahrsch. Verw. Gebiete'' , '''42''' : 3 (1978) pp. 229–260</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> E.B. Dynkin, "Boundary theory of Markov processes (the discrete case)" ''Russian Math. Surveys'' , '''24''' : 2 (1969) pp. 1–42 ''Uspekhi Mat. Nauk'' , '''24''' : 4 (1969) pp. 89–152</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> R.S. Martin, "Minimal positive harmonic functions" ''Trans. Amer. Math. Soc.'' , '''49''' (1941) pp. 137–172</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M. Motoo, "Application of additive functionals to the boundary problem of Markov processes. Lévy's system of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062560/m06256090.png" />-processes" , ''Proc. 5-th Berkeley Symp. Math. Stat. Probab.'' , '''2''' : 2 (1967) pp. 75–110</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H. Kunita, T. Watanabe, "Some theorems concerning resolvents over locally compact spaces" , ''Proc. 5-th Berkeley Symp. Math. Stat. Probab.'' , '''2''' : 2 (1967) pp. 131–164</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J.L. Doob, "Discrete potential theory and boundaries" ''J. Math. and Mech.'' , '''8''' : 3 (1959) pp. 433–458; 993</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> T. Watanabe, "On the theory of Martin boundaries induced by countable Markov processes" ''Mem. Coll. Sci. Kyoto Univ. Ser. A'' , '''33''' : 1 (1960) pp. 39–108</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> G.A. Hunt, "Markov chains and Markov boundaries" ''Illinois J. Math.'' , '''4''' (1960) pp. 313–340</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> P.L. Hennequin, A. Tortrat, "Théorie des probabilites et quelques applications" , Masson (1965)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> H. Kunita, T. Watanabe, "Markov processes and Martin boundaries I" ''Illinois J. Math.'' , '''9''' : 3 (1965) pp. 485–526</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> M.G. Shur, ''Trudy Moskov. Inst. Elektron. Mashinostr.'' , '''5''' (1970) pp. 192–251</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> T. Jeulin, "Compactification de Martin d'un processus droit" ''Z. Wahrsch. Verw. Gebiete'' , '''42''' : 3 (1978) pp. 229–260</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> E.B. Dynkin, "Boundary theory of Markov processes (the discrete case)" ''Russian Math. Surveys'' , '''24''' : 2 (1969) pp. 1–42 ''Uspekhi Mat. Nauk'' , '''24''' : 4 (1969) pp. 89–152</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Latest revision as of 07:59, 6 June 2020
The boundary of the state space of a Markov process or of its image in some compact space, constructed by a scheme similar to the Martin scheme (see [1]).
A probabilistic interpretation of Martin's construction was first proposed by J.L. Doob (see [4]), who discussed the case of discrete Markov chains.
Let $ P ( t , x , B ) $ be the transition function of a homogeneous Markov process $ X = ( x _ {t} , \zeta , F _ {t} , {\mathsf P} _ {x} ) $, given on a separable, locally compact space $ E $, where $ t \geq 0 $, $ x \in E $, $ B \in {\mathcal B} $, and $ {\mathcal B} $ is the family of Borel sets in $ E $. A function $ g _ \alpha ( x , y ) \geq 0 $ defined for $ \alpha \geq 0 $, $ x \in E $, $ y \in E $, which is $ ( {\mathcal B} \times {\mathcal B} ) $- measurable for fixed $ \alpha $ is called a Green's function if for each $ B \in {\mathcal B} $,
$$ \int\limits _ { B } g _ \alpha ( x , y ) m ( d y ) \equiv \ \int\limits _ { 0 } ^ \infty e ^ {- \alpha t } P ( t , x , B ) d t , $$
where $ m $ is a measure on $ {\mathcal B} $. To avoid ambiguity in the definition of a Green's function, it can be required in addition that for any continuous function $ f ( x) $ with compact support, the function
$$ g _ \alpha ( \cdot ) = \ \int\limits _ { E } f ( x) g _ \alpha ( x , \cdot ) m ( d x ) $$
is $ \Lambda $- continuous (meaning that there exists a function $ F ( t , \omega ) $ which is left continuous in $ t $ and such that
$$ {\mathsf P} _ {x} \{ F ( t , \omega ) \neq g _ \alpha ( x _ {t} ( \omega ) ) \} \equiv 0 ,\ \ x \in E ,\ t > 0 \textrm{ ) } . $$
Fixing a measure $ \gamma $ in $ {\mathcal B} $ and postulating the existence of a Green's function, one defines the Martin kernel
$$ K _ {y} ^ \alpha ( x) = \ \frac{g _ \alpha ( x , y ) }{q ( y ) } , $$
where
$$ q ( y) = \int\limits _ { E } g _ \alpha ( x , y ) \gamma ( d x ) $$
(here some restrictions must be introduced to ensure, in particular, the positivity and $ \Lambda $- continuity of $ q ( y) $). If $ \gamma $ is the unit measure concentrated at some point and $ X $ is a Wiener process terminating at the first exit time for some domain, then the definition of $ K _ {y} ^ {0} ( x) $ reduces to an analogous form [1]. Under broad conditions one can establish the existence of a compact set $ {\mathcal E} $( the "Martin compactum" ), a measure $ K _ {y} ^ \alpha ( d x ) $ on $ {\mathcal B} $( $ \alpha \geq 0 $, $ y \in {\mathcal E} $) and a mapping $ i : E \rightarrow {\mathcal E} $ for which: a) $ i ( E) $ is dense in $ {\mathcal E} $; b) the function
$$ K _ {y} ^ \alpha ( f ) = \ \int\limits _ {\mathcal B} f ( x) K _ {y} ^ \alpha ( d x ) $$
separates points and is continuous on $ {\mathcal E} $ as $ f $ runs through all continuous function in $ E $ with compact support; and c) the measure $ K _ {i ( y) } ^ \alpha ( d x ) $ coincides with $ K _ {y} ^ \alpha ( x) m ( d x ) $ if $ y \in E $. The boundary of the set $ i ( E) $ in $ {\mathcal E} $ is called the Martin boundary or exit-boundary (in the study of decompositions of excessive measures the dual object, the entrance-boundary, arises; see [3], [4]).
In order to describe the properties of $ {\mathcal E} $ it is convenient to invoke $ h $- processes in the sense of Doob: to each excessive function $ h $ is associated the transition function
$$ P ^ {h} ( t , x , B ) = \ h ^ {-} 1 ( x) \int\limits _ { E } h ( y) P ( t , x , d y ) $$
on $ ( E ^ {h} , {\mathcal B} ^ {h} ) $, where $ E ^ {h} = \{ {x \in E } : {0 < h ( x) < \infty } \} $ and $ {\mathcal B} ^ {h} = \{ {A \in B } : {A \subset E ^ {h} } \} $; the corresponding Markov process is an $ h $- process. All $ h $- processes can be realized, together with $ X $, on the space of elementary events, so that they are distinguished only by the families of measures $ \{ {\mathsf P} _ {x} ^ {h} \} $. One constructs in $ {\mathcal E} $ a modification of $ x _ {t} $, a left-continuous process $ z _ {t} $( $ 0 < t \leq \zeta $) for which $ {\mathsf P} _ {x} ^ {h} \{ z _ {t} \neq i ( x _ {t} ) \} \equiv 0 $ if $ h \in L _ {1} ( \gamma ) $. In the topology of $ {\mathcal E} $ the limit $ z _ \zeta = \lim\limits _ {t \uparrow \zeta } z _ {t} $ exists almost certainly.
There is a set $ U \subset {\mathcal E} $( the "exit space" ) such that: first, $ {\mathsf P} _ {x} ^ {h} \{ z _ \zeta \in U \} \equiv 1 $ for all $ h ( x) $ of the above form; secondly, the measure $ K _ {y} ^ \alpha $ for $ y \in U $ has a density $ k _ {y} ^ \alpha ( \cdot ) $ with respect to $ m $, where one can take for $ k _ {y} ^ {0} ( \cdot ) $ an excessive function whose spectral measure is the unit measure concentrated at $ y $; and thirdly, $ h ( x) $ admits a unique integral decomposition of the form
$$ h ( x) = \int\limits _ { U } k _ {y} ^ {0} ( x) \mu ( d x ) . $$
The measure $ \mu $ in the decomposition is called the spectral measure of the function $ h $; it is given by the formula
$$ \mu ( B) = \int\limits _ { E } h ( x) {\mathsf P} _ {x} ^ {h} \{ z _ \zeta \in B \} \gamma ( d x ) , $$
where $ B $ is a Borel set in $ {\mathcal E} $.
In the theory of Markov processes other types of compactifications are also used, particularly those in which any function of the form
$$ \int\limits _ { 0 } ^ \infty e ^ {- \alpha t } \ d t \int\limits _ { E } f ( y) P ( t , x , d y ) ,\ \ \alpha > 0 ,\ x \in E , $$
has a continuous extension for a sufficiently general set of functions $ f $.
References
| [1] | R.S. Martin, "Minimal positive harmonic functions" Trans. Amer. Math. Soc. , 49 (1941) pp. 137–172 |
| [2] | M. Motoo, "Application of additive functionals to the boundary problem of Markov processes. Lévy's system of 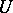 -processes" , Proc. 5-th Berkeley Symp. Math. Stat. Probab. , 2 : 2 (1967) pp. 75–110 -processes" , Proc. 5-th Berkeley Symp. Math. Stat. Probab. , 2 : 2 (1967) pp. 75–110 |
| [3] | H. Kunita, T. Watanabe, "Some theorems concerning resolvents over locally compact spaces" , Proc. 5-th Berkeley Symp. Math. Stat. Probab. , 2 : 2 (1967) pp. 131–164 |
| [4] | J.L. Doob, "Discrete potential theory and boundaries" J. Math. and Mech. , 8 : 3 (1959) pp. 433–458; 993 |
| [5] | T. Watanabe, "On the theory of Martin boundaries induced by countable Markov processes" Mem. Coll. Sci. Kyoto Univ. Ser. A , 33 : 1 (1960) pp. 39–108 |
| [6] | G.A. Hunt, "Markov chains and Markov boundaries" Illinois J. Math. , 4 (1960) pp. 313–340 |
| [7] | P.L. Hennequin, A. Tortrat, "Théorie des probabilites et quelques applications" , Masson (1965) |
| [8] | H. Kunita, T. Watanabe, "Markov processes and Martin boundaries I" Illinois J. Math. , 9 : 3 (1965) pp. 485–526 |
| [9] | M.G. Shur, Trudy Moskov. Inst. Elektron. Mashinostr. , 5 (1970) pp. 192–251 |
| [10] | T. Jeulin, "Compactification de Martin d'un processus droit" Z. Wahrsch. Verw. Gebiete , 42 : 3 (1978) pp. 229–260 |
| [11] | E.B. Dynkin, "Boundary theory of Markov processes (the discrete case)" Russian Math. Surveys , 24 : 2 (1969) pp. 1–42 Uspekhi Mat. Nauk , 24 : 4 (1969) pp. 89–152 |
Comments
One of the other types of compactifications used in the theory of Markov processes is the Ray–Knight compactification.
References
| [a1] | J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1984) |
Martin boundary in the theory of Markov processes. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Martin_boundary_in_the_theory_of_Markov_processes&oldid=47778