Difference between revisions of "Lindelöf theorem"
Ulf Rehmann (talk | contribs) m (moved Lindelof theorem to Lindelöf theorem over redirect: accented title) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | l0590001.png | ||
| + | $#A+1 = 45 n = 1 | ||
| + | $#C+1 = 45 : ~/encyclopedia/old_files/data/L059/L.0509000 Lindel\AGof theorem | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''on asymptotic values'' | ''on asymptotic values'' | ||
| − | 1) Let | + | 1) Let $ w = f ( z) $ |
| + | be a bounded regular analytic function in the unit disc $ D = \{ {z } : {| z | < 1 } \} $ | ||
| + | and let $ \alpha $ | ||
| + | be the [[Asymptotic value|asymptotic value]] of $ f ( z) $ | ||
| + | along a Jordan arc $ L $ | ||
| + | situated in $ D $ | ||
| + | and ending at a point $ e ^ {i \theta _ {0} } $, | ||
| + | that is, $ f ( z) \rightarrow \alpha $ | ||
| + | as $ z \rightarrow e ^ {i \theta _ {0} } $ | ||
| + | along $ L $. | ||
| + | Then $ \alpha $ | ||
| + | is the [[Angular boundary value|angular boundary value]] (non-tangential boundary value) of $ f ( z) $ | ||
| + | at $ e ^ {i \theta _ {0} } $, | ||
| + | that is, $ f ( z) $ | ||
| + | tends uniformly to $ \alpha $ | ||
| + | as $ z \rightarrow e ^ {i \theta _ {0} } $ | ||
| + | inside an angle with vertex $ e ^ {i \theta _ {0} } $ | ||
| + | formed by two chords of the disc $ D $. | ||
| − | The Lindelöf theorem is also true in domains | + | The Lindelöf theorem is also true in domains $ D $ |
| + | of other types, and the conditions on $ f ( z) $ | ||
| + | have been significantly weakened. For example, it is sufficient to require that $ f ( z) $ | ||
| + | is a meromorphic function in $ D $ | ||
| + | that does not assume three different values. Lindelöf's theorem can also be generalized to functions $ f ( z) $ | ||
| + | of several complex variables $ z = ( z _ {1} \dots z _ {n} ) $. | ||
| + | For example, if $ f ( z) $ | ||
| + | is a bounded holomorphic function in the ball $ D = \{ {z } : {| z | < 1 } \} $ | ||
| + | that has asymptotic value $ \alpha $ | ||
| + | along a non-tangential path $ L $ | ||
| + | at a point $ \zeta \in \partial D $, | ||
| + | then $ \alpha $ | ||
| + | is the non-tangential boundary value of $ f ( z) $ | ||
| + | at $ \zeta $( | ||
| + | see [[#References|[4]]]). | ||
| − | 2) Let | + | 2) Let $ w = f ( z) $ |
| + | be a bounded regular analytic function in the disc $ D = \{ {z } : {| z | < 1 } \} $ | ||
| + | that has asymptotic values $ \alpha $ | ||
| + | and $ \beta $ | ||
| + | along two distinct paths $ L _ {1} $ | ||
| + | and $ L _ {2} $ | ||
| + | that end at the point $ e ^ {i \theta _ {0} } $. | ||
| + | Then $ \alpha = \beta $ | ||
| + | and $ f ( z) \rightarrow \alpha $ | ||
| + | uniformly inside the angle between the paths $ L _ {1} $ | ||
| + | and $ L _ {2} $. | ||
| + | This theorem is also true for domains $ D $ | ||
| + | of other types. For unbounded functions it is false, generally speaking. | ||
These theorems were discovered by E. Lindelöf [[#References|[1]]]. | These theorems were discovered by E. Lindelöf [[#References|[1]]]. | ||
| Line 11: | Line 66: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Lindelöf, "Sur un principe générale de l'analyse et ses applications à la théorie de la représentation conforme" ''Acta Soc. Sci. Fennica'' , '''46''' : 4 (1915) pp. 1–35</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G.M. Goluzin, "Geometric theory of functions of a complex variable" , ''Transl. Math. Monogr.'' , '''26''' , Amer. Math. Soc. (1969) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 1;6</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> E.M. [E.M. Chirka] Čirka, G.M. [G.M. Khenkin] Henkin, "Boundary properties of holomorphic functions of several complex variables" ''J. Soviet Math.'' , '''5''' (1976) pp. 612–687 ''Itogi Nauk. i Tekhn. Sovrem. Probl.'' , '''4''' (1975) pp. 13–142</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Lindelöf, "Sur un principe générale de l'analyse et ses applications à la théorie de la représentation conforme" ''Acta Soc. Sci. Fennica'' , '''46''' : 4 (1915) pp. 1–35</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G.M. Goluzin, "Geometric theory of functions of a complex variable" , ''Transl. Math. Monogr.'' , '''26''' , Amer. Math. Soc. (1969) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 1;6</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> E.M. [E.M. Chirka] Čirka, G.M. [G.M. Khenkin] Henkin, "Boundary properties of holomorphic functions of several complex variables" ''J. Soviet Math.'' , '''5''' (1976) pp. 612–687 ''Itogi Nauk. i Tekhn. Sovrem. Probl.'' , '''4''' (1975) pp. 13–142</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | For the generalization of Lindelöf's theorem to functions of several variables, the condition that the path | + | For the generalization of Lindelöf's theorem to functions of several variables, the condition that the path $ L $ |
| + | is non-tangential may be weakened, see [[#References|[a1]]], Chapt. 8. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Rudin, "Function theory in the unit ball in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059000/l05900046.png" />" , Springer (1980)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Rudin, "Function theory in the unit ball in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l059/l059000/l05900046.png" />" , Springer (1980)</TD></TR></table> | ||
Revision as of 22:16, 5 June 2020
on asymptotic values
1) Let $ w = f ( z) $ be a bounded regular analytic function in the unit disc $ D = \{ {z } : {| z | < 1 } \} $ and let $ \alpha $ be the asymptotic value of $ f ( z) $ along a Jordan arc $ L $ situated in $ D $ and ending at a point $ e ^ {i \theta _ {0} } $, that is, $ f ( z) \rightarrow \alpha $ as $ z \rightarrow e ^ {i \theta _ {0} } $ along $ L $. Then $ \alpha $ is the angular boundary value (non-tangential boundary value) of $ f ( z) $ at $ e ^ {i \theta _ {0} } $, that is, $ f ( z) $ tends uniformly to $ \alpha $ as $ z \rightarrow e ^ {i \theta _ {0} } $ inside an angle with vertex $ e ^ {i \theta _ {0} } $ formed by two chords of the disc $ D $.
The Lindelöf theorem is also true in domains $ D $ of other types, and the conditions on $ f ( z) $ have been significantly weakened. For example, it is sufficient to require that $ f ( z) $ is a meromorphic function in $ D $ that does not assume three different values. Lindelöf's theorem can also be generalized to functions $ f ( z) $ of several complex variables $ z = ( z _ {1} \dots z _ {n} ) $. For example, if $ f ( z) $ is a bounded holomorphic function in the ball $ D = \{ {z } : {| z | < 1 } \} $ that has asymptotic value $ \alpha $ along a non-tangential path $ L $ at a point $ \zeta \in \partial D $, then $ \alpha $ is the non-tangential boundary value of $ f ( z) $ at $ \zeta $( see [4]).
2) Let $ w = f ( z) $ be a bounded regular analytic function in the disc $ D = \{ {z } : {| z | < 1 } \} $ that has asymptotic values $ \alpha $ and $ \beta $ along two distinct paths $ L _ {1} $ and $ L _ {2} $ that end at the point $ e ^ {i \theta _ {0} } $. Then $ \alpha = \beta $ and $ f ( z) \rightarrow \alpha $ uniformly inside the angle between the paths $ L _ {1} $ and $ L _ {2} $. This theorem is also true for domains $ D $ of other types. For unbounded functions it is false, generally speaking.
These theorems were discovered by E. Lindelöf [1].
References
| [1] | E. Lindelöf, "Sur un principe générale de l'analyse et ses applications à la théorie de la représentation conforme" Acta Soc. Sci. Fennica , 46 : 4 (1915) pp. 1–35 |
| [2] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [3] | E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 1;6 |
| [4] | E.M. [E.M. Chirka] Čirka, G.M. [G.M. Khenkin] Henkin, "Boundary properties of holomorphic functions of several complex variables" J. Soviet Math. , 5 (1976) pp. 612–687 Itogi Nauk. i Tekhn. Sovrem. Probl. , 4 (1975) pp. 13–142 |
Comments
For the generalization of Lindelöf's theorem to functions of several variables, the condition that the path $ L $ is non-tangential may be weakened, see [a1], Chapt. 8.
References
| [a1] | W. Rudin, "Function theory in the unit ball in 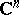 " , Springer (1980) " , Springer (1980) |
Lindelöf theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lindel%C3%B6f_theorem&oldid=47644