Difference between revisions of "Interpolation spline"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | i0519801.png | ||
| + | $#A+1 = 32 n = 1 | ||
| + | $#C+1 = 32 : ~/encyclopedia/old_files/data/I051/I.0501980 Interpolation spline | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
A spline | A spline | ||
| − | + | $$ | |
| + | S _ {m} ( \Delta _ {n} ; x ) = \ | ||
| + | a _ {0} + a _ {1} x + \dots | ||
| + | + a _ {m-} 1 x ^ {m-} 1 + | ||
| + | \sum _ { k= } 0 ^ { n- } 1 | ||
| + | C _ {k} ( x - x _ {k} ) _ {+} ^ {m} , | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | t _ {+} = \ | ||
| + | \left \{ | ||
| + | \begin{array}{ll} | ||
| + | t & t \geq 0 , \\ | ||
| + | 0 & t < 0 , \\ | ||
| + | \end{array} | ||
| + | \ \ | ||
| + | x _ {0} < \dots < x _ {n} , | ||
| + | \right .$$ | ||
| − | that coincides with a given function at given distinct points | + | that coincides with a given function at given distinct points $ \{ \overline{x}\; _ {i} \} $. |
| + | For $ m = 2 k + 1 $ | ||
| + | one usually takes $ \overline{x}\; _ {i} = x _ {i} $, | ||
| + | $ i = 0 \dots n $, | ||
| + | and since for $ S _ {2k+} 1 ( \Delta _ {n} ; x ) $ | ||
| + | there still are $ 2 k $ | ||
| + | free parameters, one prescribes $ k $ | ||
| + | additional conditions at $ x _ {0} $ | ||
| + | and $ x _ {n} $, | ||
| + | e.g. $ S _ {2k+} 1 ^ {(} j) ( \Delta _ {n} ; z ) = y _ {z} ^ {(} j) $, | ||
| + | $ j = 1 \dots k $, | ||
| + | $ z = x _ {0} , x _ {n} $, | ||
| + | where $ y _ {z} ^ {(} j) $ | ||
| + | are given numbers. If the $ y _ {z} ^ {(} j) $ | ||
| + | linearly depend on the given function, then the corresponding spline linearly depends on this function. For $ m = 2 k $ | ||
| + | one usually takes $ \overline{x}\; _ {0} = x _ {0} $, | ||
| + | $ \overline{x}\; _ {n} = x _ {n} $ | ||
| + | and $ x _ {i} = ( \overline{x}\; _ {i-} 1 + \overline{x}\; _ {i} ) / 2 $, | ||
| + | $ i = 1 \dots n - 1 $, | ||
| + | and $ k $ | ||
| + | additional conditions are prescribed at $ x _ {0} $ | ||
| + | and $ x _ {n} $. | ||
| + | If the spline $ S _ {m} ( \Delta _ {n} ; x ) $ | ||
| + | has an $ ( m - s ) $- | ||
| + | th continuous and an $ ( m - s + 1 ) $- | ||
| + | st discontinuous derivative at $ x _ {1} \dots x _ {n-} 1 $, | ||
| + | then for $ s \geq 2 $ | ||
| + | the first $ ( s - 1 ) $- | ||
| + | st derivatives of the spline are prescribed at these points, requiring them to coincide with the corresponding derivatives of the function to be interpolated. Interpolation $ L $- | ||
| + | and $ L _ {q} $- | ||
| + | splines, as well as interpolation splines in several variables, have also been considered. Interpolation splines are used to approximate a function using its values on a grid. In contrast to interpolation polynomials, there exist matrices of nodes such that the interpolation splines converge to an arbitrary given continuous integrable function. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.B. Stechkin, Yu.N. Subbotin, "Splines in numerical mathematics" , Moscow (1976) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.H. Ahlberg, E.N. Nilson, J.F. Walsh, "Theory of splines and their applications" , Acad. Press (1967)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.B. Stechkin, Yu.N. Subbotin, "Splines in numerical mathematics" , Moscow (1976) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.H. Ahlberg, E.N. Nilson, J.F. Walsh, "Theory of splines and their applications" , Acad. Press (1967)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Revision as of 22:13, 5 June 2020
A spline
$$ S _ {m} ( \Delta _ {n} ; x ) = \ a _ {0} + a _ {1} x + \dots + a _ {m-} 1 x ^ {m-} 1 + \sum _ { k= } 0 ^ { n- } 1 C _ {k} ( x - x _ {k} ) _ {+} ^ {m} , $$
where
$$ t _ {+} = \ \left \{ \begin{array}{ll} t & t \geq 0 , \\ 0 & t < 0 , \\ \end{array} \ \ x _ {0} < \dots < x _ {n} , \right .$$
that coincides with a given function at given distinct points $ \{ \overline{x}\; _ {i} \} $. For $ m = 2 k + 1 $ one usually takes $ \overline{x}\; _ {i} = x _ {i} $, $ i = 0 \dots n $, and since for $ S _ {2k+} 1 ( \Delta _ {n} ; x ) $ there still are $ 2 k $ free parameters, one prescribes $ k $ additional conditions at $ x _ {0} $ and $ x _ {n} $, e.g. $ S _ {2k+} 1 ^ {(} j) ( \Delta _ {n} ; z ) = y _ {z} ^ {(} j) $, $ j = 1 \dots k $, $ z = x _ {0} , x _ {n} $, where $ y _ {z} ^ {(} j) $ are given numbers. If the $ y _ {z} ^ {(} j) $ linearly depend on the given function, then the corresponding spline linearly depends on this function. For $ m = 2 k $ one usually takes $ \overline{x}\; _ {0} = x _ {0} $, $ \overline{x}\; _ {n} = x _ {n} $ and $ x _ {i} = ( \overline{x}\; _ {i-} 1 + \overline{x}\; _ {i} ) / 2 $, $ i = 1 \dots n - 1 $, and $ k $ additional conditions are prescribed at $ x _ {0} $ and $ x _ {n} $. If the spline $ S _ {m} ( \Delta _ {n} ; x ) $ has an $ ( m - s ) $- th continuous and an $ ( m - s + 1 ) $- st discontinuous derivative at $ x _ {1} \dots x _ {n-} 1 $, then for $ s \geq 2 $ the first $ ( s - 1 ) $- st derivatives of the spline are prescribed at these points, requiring them to coincide with the corresponding derivatives of the function to be interpolated. Interpolation $ L $- and $ L _ {q} $- splines, as well as interpolation splines in several variables, have also been considered. Interpolation splines are used to approximate a function using its values on a grid. In contrast to interpolation polynomials, there exist matrices of nodes such that the interpolation splines converge to an arbitrary given continuous integrable function.
References
| [1] | S.B. Stechkin, Yu.N. Subbotin, "Splines in numerical mathematics" , Moscow (1976) (In Russian) |
| [2] | J.H. Ahlberg, E.N. Nilson, J.F. Walsh, "Theory of splines and their applications" , Acad. Press (1967) |
Comments
Cf. also Spline; Spline approximation; Spline interpolation.
References
| [a1] | C. de Boor, "Splines as linear combinations of 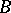 -splines, a survey" G.G. Lorentz (ed.) C.K. Chri (ed.) L.L. Schumaker (ed.) , Approximation theory , 2 , Acad. Press (1976) -splines, a survey" G.G. Lorentz (ed.) C.K. Chri (ed.) L.L. Schumaker (ed.) , Approximation theory , 2 , Acad. Press (1976) |
| [a2] | I.J. Schoenberg, "Cardinal spline interpolation" , SIAM (1973) |
| [a3] | L.L. Schumaker, "Spline functions, basic theory" , Wiley (1981) |
Interpolation spline. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Interpolation_spline&oldid=47396