Difference between revisions of "Homology of a dynamical system"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | h0478201.png | ||
| + | $#A+1 = 14 n = 1 | ||
| + | $#C+1 = 14 : ~/encyclopedia/old_files/data/H047/H.0407820 Homology of a dynamical system, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''cohomology of a dynamical system'' | ''cohomology of a dynamical system'' | ||
| − | One of the invariants in [[Ergodic theory|ergodic theory]], the construction of which recalls the construction of the cohomology of a group [[#References|[1]]]. In the simplest case of the one-dimensional (co)homology group | + | One of the invariants in [[Ergodic theory|ergodic theory]], the construction of which recalls the construction of the cohomology of a group [[#References|[1]]]. In the simplest case of the one-dimensional (co)homology group $ H ^ {1} ( T, X) $ |
| + | of the cascade obtained by iterating an automorphism $ T $ | ||
| + | of a measure space $ X $, | ||
| + | the definition is equivalent to the following one. Let $ Z( X) $ | ||
| + | be the additive group of all measurable functions on $ X $( | ||
| + | or, respectively, the multiplicative group of all measurable functions $ f $ | ||
| + | for which $ | f( x) | = 1 $ | ||
| + | almost-everywhere). The additive (multiplicative) (co) boundary of a function $ f $ | ||
| + | is the function $ g( x) = f( Tx) - f( x) $( | ||
| + | or, respectively, $ g( x) = f( Tx)/f( x) $). | ||
| + | If one denotes the set of all (co)boundaries by $ B( T, X) $, | ||
| + | then one may define the additive (or, respectively, multiplicative) (co)homology group $ H ^ {1} ( T, X) $ | ||
| + | as the quotient group $ Z( X)/B( T, X) $. | ||
| + | Narrower classes of functions rather than all measurable functions may also be considered. The homology groups of a dynamical system are invariants of a trajectory isomorphism (for details on $ H ^ {1} $ | ||
| + | see [[#References|[2]]]). | ||
The homology of a dynamical system has not yet (1977) been computed for even a single non-trivial example. The use of "homological" concepts in ergodic theory stems from the fact that in many real cases it may be important to know (and it is sometimes actually known) whether some given function is or is not a coboundary. | The homology of a dynamical system has not yet (1977) been computed for even a single non-trivial example. The use of "homological" concepts in ergodic theory stems from the fact that in many real cases it may be important to know (and it is sometimes actually known) whether some given function is or is not a coboundary. | ||
| Line 7: | Line 33: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Kirillov, "Dynamical systems, factors and representations of groups" ''Russian Math. Surveys'' , '''22''' : 5 (1967) pp. 63–75 ''Uspekhi Mat. Nauk'' , '''22''' : 5 (1967) pp. 67–80</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.M. Stepin, "Cohomologies of automorphism groups of a Lebesgue space" ''Funct. Anal. Appl.'' , '''5''' (1971) pp. 167–168 ''Funktsional. Anal. i Prilozhen.'' , '''5''' : 2 (1971) pp. 91–92</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Kirillov, "Dynamical systems, factors and representations of groups" ''Russian Math. Surveys'' , '''22''' : 5 (1967) pp. 63–75 ''Uspekhi Mat. Nauk'' , '''22''' : 5 (1967) pp. 67–80</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.M. Stepin, "Cohomologies of automorphism groups of a Lebesgue space" ''Funct. Anal. Appl.'' , '''5''' (1971) pp. 167–168 ''Funktsional. Anal. i Prilozhen.'' , '''5''' : 2 (1971) pp. 91–92</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Latest revision as of 22:10, 5 June 2020
cohomology of a dynamical system
One of the invariants in ergodic theory, the construction of which recalls the construction of the cohomology of a group [1]. In the simplest case of the one-dimensional (co)homology group $ H ^ {1} ( T, X) $ of the cascade obtained by iterating an automorphism $ T $ of a measure space $ X $, the definition is equivalent to the following one. Let $ Z( X) $ be the additive group of all measurable functions on $ X $( or, respectively, the multiplicative group of all measurable functions $ f $ for which $ | f( x) | = 1 $ almost-everywhere). The additive (multiplicative) (co) boundary of a function $ f $ is the function $ g( x) = f( Tx) - f( x) $( or, respectively, $ g( x) = f( Tx)/f( x) $). If one denotes the set of all (co)boundaries by $ B( T, X) $, then one may define the additive (or, respectively, multiplicative) (co)homology group $ H ^ {1} ( T, X) $ as the quotient group $ Z( X)/B( T, X) $. Narrower classes of functions rather than all measurable functions may also be considered. The homology groups of a dynamical system are invariants of a trajectory isomorphism (for details on $ H ^ {1} $ see [2]).
The homology of a dynamical system has not yet (1977) been computed for even a single non-trivial example. The use of "homological" concepts in ergodic theory stems from the fact that in many real cases it may be important to know (and it is sometimes actually known) whether some given function is or is not a coboundary.
References
| [1] | A.A. Kirillov, "Dynamical systems, factors and representations of groups" Russian Math. Surveys , 22 : 5 (1967) pp. 63–75 Uspekhi Mat. Nauk , 22 : 5 (1967) pp. 67–80 |
| [2] | A.M. Stepin, "Cohomologies of automorphism groups of a Lebesgue space" Funct. Anal. Appl. , 5 (1971) pp. 167–168 Funktsional. Anal. i Prilozhen. , 5 : 2 (1971) pp. 91–92 |
Comments
For related results on cocycles, see e.g. [a1] and the references given there (e.g., to work of G.W. Mackey).
The study of cohomology for abstract (minimal) topological dynamical systems (i.e., dynamical systems consisting of arbitrary topological groups acting on a compact space) was initiated in [a3]. For further developments, see [a2].
References
| [a1] | V.Ya. Golodets, S.D. Sinelshchikov, "Locally compact groups appearing as ranges of cocycles of ergodic 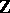 -actions" Ergodic Theory and Dynamical Systems , 5 (1985) pp. 47–57 -actions" Ergodic Theory and Dynamical Systems , 5 (1985) pp. 47–57 |
| [a2] | R. Ellis, "Cohomology of groups and almost periodic extensions of minimal sets" Ergodic Theory and Dynamical Systems , 1 (1981) pp. 49–64 |
| [a3] | K.E. Petersen, "Extension of minimal transformation groups" Math. Systems Theory , 5 (1971) pp. 365–375 |
Homology of a dynamical system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Homology_of_a_dynamical_system&oldid=47259