Difference between revisions of "Holomorphically-convex complex space"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | h0475701.png | ||
| + | $#A+1 = 20 n = 1 | ||
| + | $#C+1 = 20 : ~/encyclopedia/old_files/data/H047/H.0407570 Holomorphically\AAhconvex complex space | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A [[Complex space|complex space]] $ X $ | |
| + | that satisfies the following condition: For each compactum $ K \subset X $ | ||
| + | the set | ||
| − | + | $$ | |
| + | \left \{ {x \in X } : {| f ( x) | \leq | ||
| + | \sup _ { K } | f | ( f \in A) } \right \} | ||
| + | , | ||
| + | $$ | ||
| − | + | where $ A $ | |
| + | is the algebra of holomorphic functions on $ X $, | ||
| + | is compact. A space $ X $ | ||
| + | is holomorphically convex if and only if it admits a proper surjective holomorphic mapping $ \phi $ | ||
| + | onto some [[Stein space|Stein space]] (a holomorphically-complete space) $ \widetilde{X} $ | ||
| + | which induces an isomorphism between the algebras of holomorphic functions on these spaces. The mapping $ \phi : X \rightarrow \widetilde{X} $( | ||
| + | the holomorphic reduction of $ X $) | ||
| + | is uniquely defined and has connected fibres [[#References|[1]]]. For any [[Coherent analytic sheaf|coherent analytic sheaf]] $ F $ | ||
| + | on a holomorphically-convex complex space $ X $, | ||
| + | the cohomology spaces $ H ^ {p} ( X, F ) $ | ||
| + | and $ H _ {c} ^ {p} ( X, F ) $, | ||
| + | $ p \geq 0 $, | ||
| + | are separable topological vector spaces [[#References|[2]]]. | ||
| − | for any coherent analytic sheaf | + | A special class of holomorphically-convex complex spaces is formed by the complex spaces $ X $ |
| + | for which the holomorphic reduction mapping is bijective outside some compact analytic set (such a space is obtained from a Stein space by a proper [[Modification|modification]] which blows-up a finite number of points). A complex space possesses this property if and only if | ||
| + | |||
| + | $$ | ||
| + | \mathop{\rm dim} H ^ {p} ( X, F ) < \infty ,\ \ | ||
| + | p > 0, | ||
| + | $$ | ||
| + | |||
| + | for any coherent analytic sheaf $ F $ | ||
| + | on $ X $[[#References|[3]]]. This class of complex spaces also coincides with the class of strictly $ 1 $- | ||
| + | convex complex spaces (cf. [[Pseudo-convex and pseudo-concave|Pseudo-convex and pseudo-concave]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Cartan, "Quotients of complex analytic spaces" , ''Contributions to function theory. Internat. Colloq. Function Theory, Bombay 1960'' , Tata Inst. (1960) pp. 1–15</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.P. Ramis, "Théorèmes de séperation et de finitude pour l'homologie et la cohomologie des espaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047570/h04757022.png" />-convexes-concaves" ''Ann. Scuola Norm. Sup. Pisa Ser. 3'' , '''27''' (1973) pp. 933–997</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> R. Narasimhan, "The Levi problem for complex spaces II" ''Math. Ann.'' , '''146''' (1962) pp. 195–216</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Cartan, "Quotients of complex analytic spaces" , ''Contributions to function theory. Internat. Colloq. Function Theory, Bombay 1960'' , Tata Inst. (1960) pp. 1–15</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.P. Ramis, "Théorèmes de séperation et de finitude pour l'homologie et la cohomologie des espaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047570/h04757022.png" />-convexes-concaves" ''Ann. Scuola Norm. Sup. Pisa Ser. 3'' , '''27''' (1973) pp. 933–997</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> R. Narasimhan, "The Levi problem for complex spaces II" ''Math. Ann.'' , '''146''' (1962) pp. 195–216</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) pp. Chapt. 1, Sect. G</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> H. Grauert, R. Remmert, "Theory of Stein spaces" , Springer (1979) (Translated from German)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H. Grauert, R. Remmert, "Komplexe Räume" ''Math. Ann.'' , '''136''' (1958) pp. 245–318</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) pp. Chapt. 1, Sect. G</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> H. Grauert, R. Remmert, "Theory of Stein spaces" , Springer (1979) (Translated from German)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H. Grauert, R. Remmert, "Komplexe Räume" ''Math. Ann.'' , '''136''' (1958) pp. 245–318</TD></TR></table> | ||
Latest revision as of 22:10, 5 June 2020
A complex space $ X $
that satisfies the following condition: For each compactum $ K \subset X $
the set
$$ \left \{ {x \in X } : {| f ( x) | \leq \sup _ { K } | f | ( f \in A) } \right \} , $$
where $ A $ is the algebra of holomorphic functions on $ X $, is compact. A space $ X $ is holomorphically convex if and only if it admits a proper surjective holomorphic mapping $ \phi $ onto some Stein space (a holomorphically-complete space) $ \widetilde{X} $ which induces an isomorphism between the algebras of holomorphic functions on these spaces. The mapping $ \phi : X \rightarrow \widetilde{X} $( the holomorphic reduction of $ X $) is uniquely defined and has connected fibres [1]. For any coherent analytic sheaf $ F $ on a holomorphically-convex complex space $ X $, the cohomology spaces $ H ^ {p} ( X, F ) $ and $ H _ {c} ^ {p} ( X, F ) $, $ p \geq 0 $, are separable topological vector spaces [2].
A special class of holomorphically-convex complex spaces is formed by the complex spaces $ X $ for which the holomorphic reduction mapping is bijective outside some compact analytic set (such a space is obtained from a Stein space by a proper modification which blows-up a finite number of points). A complex space possesses this property if and only if
$$ \mathop{\rm dim} H ^ {p} ( X, F ) < \infty ,\ \ p > 0, $$
for any coherent analytic sheaf $ F $ on $ X $[3]. This class of complex spaces also coincides with the class of strictly $ 1 $- convex complex spaces (cf. Pseudo-convex and pseudo-concave).
References
| [1] | H. Cartan, "Quotients of complex analytic spaces" , Contributions to function theory. Internat. Colloq. Function Theory, Bombay 1960 , Tata Inst. (1960) pp. 1–15 |
| [2] | J.P. Ramis, "Théorèmes de séperation et de finitude pour l'homologie et la cohomologie des espaces 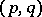 -convexes-concaves" Ann. Scuola Norm. Sup. Pisa Ser. 3 , 27 (1973) pp. 933–997 -convexes-concaves" Ann. Scuola Norm. Sup. Pisa Ser. 3 , 27 (1973) pp. 933–997 |
| [3] | R. Narasimhan, "The Levi problem for complex spaces II" Math. Ann. , 146 (1962) pp. 195–216 |
Comments
References
| [a1] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) pp. Chapt. 1, Sect. G |
| [a2] | H. Grauert, R. Remmert, "Theory of Stein spaces" , Springer (1979) (Translated from German) |
| [a3] | H. Grauert, R. Remmert, "Komplexe Räume" Math. Ann. , 136 (1958) pp. 245–318 |
Holomorphically-convex complex space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Holomorphically-convex_complex_space&oldid=47246