|
|
| Line 1: |
Line 1: |
| − | A mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h0475601.png" /> of a domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h0475602.png" /> into a domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h0475603.png" /> under which
| + | <!-- |
| | + | h0475601.png |
| | + | $#A+1 = 57 n = 1 |
| | + | $#C+1 = 57 : ~/encyclopedia/old_files/data/H047/H.0407560 Holomorphic mapping |
| | + | Automatically converted into TeX, above some diagnostics. |
| | + | Please remove this comment and the {{TEX|auto}} line below, |
| | + | if TeX found to be correct. |
| | + | --> |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h0475604.png" /></td> </tr></table>
| + | {{TEX|auto}} |
| | + | {{TEX|done}} |
| | | | |
| − | where all coordinate functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h0475605.png" /> are holomorphic in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h0475606.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h0475607.png" />, a holomorphic mapping coincides with a holomorphic function (cf. [[Analytic function|Analytic function]]).
| + | A mapping $ f: D \rightarrow D ^ { \prime } $ |
| | + | of a domain $ D \subset \mathbf C ^ {n} $ |
| | + | into a domain $ D ^ { \prime } \subset \mathbf C ^ {m} $ |
| | + | under which |
| | | | |
| − | A holomorphic mapping is called non-degenerate at a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h0475608.png" /> if the rank of the Jacobian matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h0475609.png" /> is maximal at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756010.png" /> (and hence equals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756011.png" />). A holomorphic mapping is said to be non-degenerate in the domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756012.png" /> if it is non-degenerate at all points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756013.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756014.png" />, the non-degeneracy of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756015.png" /> is equivalent to the condition
| + | $$ |
| | + | z = ( z _ {1} \dots z _ {n} ) \rightarrow \ |
| | + | ( f _ {1} ( z) \dots f _ {m} ( z)), |
| | + | $$ |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756016.png" /></td> </tr></table>
| + | where all coordinate functions $ f _ {1} \dots f _ {m} $ |
| | + | are holomorphic in $ D $. |
| | + | If $ m = 1 $, |
| | + | a holomorphic mapping coincides with a holomorphic function (cf. [[Analytic function|Analytic function]]). |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756017.png" />, a non-degenerate holomorphic mapping is a conformal mapping. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756018.png" />, a non-degenerate holomorphic mapping does not, in general, preserve angles between directions. If a holomorphic mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756019.png" /> is non-degenerate at a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756020.png" /> and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756021.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756022.png" /> is locally invertible, i.e., then there exist neighbourhoods <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756023.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756024.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756025.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756026.png" />, and a holomorphic mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756027.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756028.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756029.png" />. If a holomorphic mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756030.png" /> maps <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756031.png" /> onto <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756032.png" /> in a one-to-one correspondence and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756033.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756034.png" /> is non-degenerate in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756035.png" />; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756036.png" />, this is not true, e.g. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756037.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756038.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756039.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756040.png" /> and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756041.png" /> is non-degenerate in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756042.png" />, then the image of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756043.png" /> is also a domain in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756044.png" />; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756045.png" />, the principle of invariance of domain does not hold for mappings that are degenerate at certain points, e.g. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756046.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756047.png" />.
| + | A holomorphic mapping is called non-degenerate at a point $ z \in D $ |
| | + | if the rank of the Jacobian matrix $ \| \partial f / \partial z \| $ |
| | + | is maximal at $ z $( |
| | + | and hence equals $ \min ( n, m) $). |
| | + | A holomorphic mapping is said to be non-degenerate in the domain $ D $ |
| | + | if it is non-degenerate at all points $ z \in D $. |
| | + | If $ m = n $, |
| | + | the non-degeneracy of $ f $ |
| | + | is equivalent to the condition |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756048.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756049.png" /> are complex manifolds, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756050.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756051.png" /> are atlases of their local coordinate systems (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756052.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756053.png" /> are homeomorphisms; cf. [[Manifold|Manifold]]), then a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756054.png" /> is said to be holomorphic if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756055.png" /> is a holomorphic mapping for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756056.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047560/h04756057.png" />. Holomorphic mappings of complex spaces are defined in a similar manner (cf. [[Analytic mapping|Analytic mapping]]). See also [[Biholomorphic mapping|Biholomorphic mapping]]. | + | $$ |
| | + | \mathop{\rm det} \left \| |
| | + | \frac{\partial f }{\partial z } |
| | + | \ |
| | + | \right \| \neq 0. |
| | + | $$ |
| | + | |
| | + | If $ n = m = 1 $, |
| | + | a non-degenerate holomorphic mapping is a conformal mapping. If $ n = m \geq 2 $, |
| | + | a non-degenerate holomorphic mapping does not, in general, preserve angles between directions. If a holomorphic mapping $ f $ |
| | + | is non-degenerate at a point $ a \in D $ |
| | + | and if $ m = n $, |
| | + | then $ f $ |
| | + | is locally invertible, i.e., then there exist neighbourhoods $ U $, |
| | + | $ U ^ { \prime } $, |
| | + | $ a \in U \subset D $, |
| | + | $ f( a) \in U ^ { \prime } \subset D ^ { \prime } $, |
| | + | and a holomorphic mapping $ f ^ { - 1 } : U ^ { \prime } \rightarrow U $ |
| | + | such that $ f ^ { - 1 } \circ f( z) = z $ |
| | + | for all $ z \in U $. |
| | + | If a holomorphic mapping $ f $ |
| | + | maps $ D $ |
| | + | onto $ f( D) $ |
| | + | in a one-to-one correspondence and if $ m = n $, |
| | + | then $ f $ |
| | + | is non-degenerate in $ D $; |
| | + | if $ m > n $, |
| | + | this is not true, e.g. $ z \rightarrow ( z ^ {2} , z ^ {3} ) $, |
| | + | $ D = \mathbf C $, |
| | + | $ D ^ { \prime } = \mathbf C ^ {2} $. |
| | + | If $ m \leq n $ |
| | + | and if $ f $ |
| | + | is non-degenerate in $ D $, |
| | + | then the image of $ D $ |
| | + | is also a domain in $ \mathbf C ^ {m} $; |
| | + | if $ m > 1 $, |
| | + | the principle of invariance of domain does not hold for mappings that are degenerate at certain points, e.g. $ ( z _ {1} , z _ {2} ) \rightarrow ( z _ {1} , z _ {1} z _ {2} ) $, |
| | + | $ D = D ^ { \prime } = \mathbf C ^ {2} $. |
| | + | |
| | + | If $ M $ |
| | + | and $ M ^ { \prime } $ |
| | + | are complex manifolds, $ \{ ( U _ \alpha , \phi _ \alpha ) \} $ |
| | + | and $ \{ ( U _ \beta ^ { \prime } , \phi _ \beta ^ \prime ) \} $ |
| | + | are atlases of their local coordinate systems ( $ \phi _ \alpha : U _ \alpha \rightarrow D _ \alpha \subset \mathbf C ^ {n} $, |
| | + | $ \phi _ \beta ^ \prime : U _ \beta ^ { \prime } \rightarrow D _ \beta ^ { \prime } \subset \mathbf C ^ {m} $ |
| | + | are homeomorphisms; cf. [[Manifold|Manifold]]), then a mapping $ f: M \rightarrow M ^ { \prime } $ |
| | + | is said to be holomorphic if $ \phi _ \beta ^ \prime \circ f \circ \phi _ \alpha ^ {-} 1 : D _ \alpha \rightarrow D _ \beta ^ { \prime } $ |
| | + | is a holomorphic mapping for all $ \alpha $ |
| | + | and $ \beta $. |
| | + | Holomorphic mappings of complex spaces are defined in a similar manner (cf. [[Analytic mapping|Analytic mapping]]). See also [[Biholomorphic mapping|Biholomorphic mapping]]. |
| | | | |
| | ====References==== | | ====References==== |
| | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965)</TD></TR></table> | | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965)</TD></TR></table> |
| − |
| |
| − |
| |
| | | | |
| | ====Comments==== | | ====Comments==== |
A mapping $ f: D \rightarrow D ^ { \prime } $
of a domain $ D \subset \mathbf C ^ {n} $
into a domain $ D ^ { \prime } \subset \mathbf C ^ {m} $
under which
$$
z = ( z _ {1} \dots z _ {n} ) \rightarrow \
( f _ {1} ( z) \dots f _ {m} ( z)),
$$
where all coordinate functions $ f _ {1} \dots f _ {m} $
are holomorphic in $ D $.
If $ m = 1 $,
a holomorphic mapping coincides with a holomorphic function (cf. Analytic function).
A holomorphic mapping is called non-degenerate at a point $ z \in D $
if the rank of the Jacobian matrix $ \| \partial f / \partial z \| $
is maximal at $ z $(
and hence equals $ \min ( n, m) $).
A holomorphic mapping is said to be non-degenerate in the domain $ D $
if it is non-degenerate at all points $ z \in D $.
If $ m = n $,
the non-degeneracy of $ f $
is equivalent to the condition
$$
\mathop{\rm det} \left \|
\frac{\partial f }{\partial z }
\
\right \| \neq 0.
$$
If $ n = m = 1 $,
a non-degenerate holomorphic mapping is a conformal mapping. If $ n = m \geq 2 $,
a non-degenerate holomorphic mapping does not, in general, preserve angles between directions. If a holomorphic mapping $ f $
is non-degenerate at a point $ a \in D $
and if $ m = n $,
then $ f $
is locally invertible, i.e., then there exist neighbourhoods $ U $,
$ U ^ { \prime } $,
$ a \in U \subset D $,
$ f( a) \in U ^ { \prime } \subset D ^ { \prime } $,
and a holomorphic mapping $ f ^ { - 1 } : U ^ { \prime } \rightarrow U $
such that $ f ^ { - 1 } \circ f( z) = z $
for all $ z \in U $.
If a holomorphic mapping $ f $
maps $ D $
onto $ f( D) $
in a one-to-one correspondence and if $ m = n $,
then $ f $
is non-degenerate in $ D $;
if $ m > n $,
this is not true, e.g. $ z \rightarrow ( z ^ {2} , z ^ {3} ) $,
$ D = \mathbf C $,
$ D ^ { \prime } = \mathbf C ^ {2} $.
If $ m \leq n $
and if $ f $
is non-degenerate in $ D $,
then the image of $ D $
is also a domain in $ \mathbf C ^ {m} $;
if $ m > 1 $,
the principle of invariance of domain does not hold for mappings that are degenerate at certain points, e.g. $ ( z _ {1} , z _ {2} ) \rightarrow ( z _ {1} , z _ {1} z _ {2} ) $,
$ D = D ^ { \prime } = \mathbf C ^ {2} $.
If $ M $
and $ M ^ { \prime } $
are complex manifolds, $ \{ ( U _ \alpha , \phi _ \alpha ) \} $
and $ \{ ( U _ \beta ^ { \prime } , \phi _ \beta ^ \prime ) \} $
are atlases of their local coordinate systems ( $ \phi _ \alpha : U _ \alpha \rightarrow D _ \alpha \subset \mathbf C ^ {n} $,
$ \phi _ \beta ^ \prime : U _ \beta ^ { \prime } \rightarrow D _ \beta ^ { \prime } \subset \mathbf C ^ {m} $
are homeomorphisms; cf. Manifold), then a mapping $ f: M \rightarrow M ^ { \prime } $
is said to be holomorphic if $ \phi _ \beta ^ \prime \circ f \circ \phi _ \alpha ^ {-} 1 : D _ \alpha \rightarrow D _ \beta ^ { \prime } $
is a holomorphic mapping for all $ \alpha $
and $ \beta $.
Holomorphic mappings of complex spaces are defined in a similar manner (cf. Analytic mapping). See also Biholomorphic mapping.
References
| [1] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) |
A non-degenerate mapping is also called non-singular.
References
| [a1] | W. Rudin, "Function theory in the unit ball in 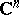 " , Springer (1980) pp. Chapt. 15 " , Springer (1980) pp. Chapt. 15 |
| [a2] | S.G. Krantz, "Function theory of several complex variables" , Wiley (1982) |
 " , Springer (1980) pp. Chapt. 15
" , Springer (1980) pp. Chapt. 15