Difference between revisions of "Feynman integral"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | f0384701.png | ||
| + | $#A+1 = 53 n = 1 | ||
| + | $#C+1 = 53 : ~/encyclopedia/old_files/data/F038/F.0308470 Feynman integral, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''Feynman path integral'' | ''Feynman path integral'' | ||
| Line 5: | Line 17: | ||
Suppose that one is given an equation | Suppose that one is given an equation | ||
| − | + | $$ \tag{1 } | |
| + | |||
| + | \frac{du }{dt } | ||
| + | = Hu, | ||
| + | $$ | ||
| + | |||
| + | where $ 0 \leq t \leq T $, | ||
| + | $ T > 0 $, | ||
| + | and $ u ( t, \omega ) $ | ||
| + | is a function defined on $ T \times \Omega $, | ||
| + | where $ \Omega \ni \omega $ | ||
| + | is some space and $ H $ | ||
| + | is a linear operator acting in a suitable way on a selected space of functions on $ \Omega $. | ||
| + | In a number of cases the transition function $ G ( \omega _ {1} , \omega _ {2} , t) $ | ||
| + | of equation (1) (that is, the kernel operator of the semi-group $ \mathop{\rm exp} \{ tH \} $, | ||
| + | $ t \geq 0 $) | ||
| + | can be represented in the form of a path integral | ||
| − | + | $$ \tag{2 } | |
| + | G ( \omega _ {1} , \omega _ {2} , t) = \ | ||
| + | \int\limits _ {\begin{array}{c} | ||
| + | \omega : \\ | ||
| + | \omega ( 0) = \omega _ {1} \\ | ||
| − | + | \omega ( t) = \omega _ {2} | |
| + | \end{array} | ||
| + | } \mathop{\rm exp} | ||
| + | \left \{ \int\limits _ { 0 } ^ { t } | ||
| + | W [ \omega ( \tau )] d \tau \right \} | ||
| + | \mu _ {\omega _ {1} , \omega _ {2} , t } | ||
| + | ( d \omega ), | ||
| + | $$ | ||
| − | where | + | where $ W ( \cdot ) $ |
| + | is some function defined on $ \Omega $, | ||
| + | the integration is carried out over the set of "trajectories" $ \omega ( \tau ) $, | ||
| + | $ 0 \leq \tau \leq t $, | ||
| + | with values in $ \Omega $, | ||
| + | "leaving" $ \omega _ {1} $ | ||
| + | at time zero and "arriving" at $ \omega _ {2} $ | ||
| + | at time $ t $, | ||
| + | and, finally, $ \mu _ {\omega _ {1} , \omega _ {2} , t } $ | ||
| + | is some measure (or pre-measure) given on this set of trajectories. The integral is interpreted either in the usual Lebesgue sense or in the sense prescribed by any one of the methods of path integration (see [[#References|[5]]], [[#References|[6]]]). Integrals of the form (2), and also integrals obtained from them by means of certain natural transformations (for example, changing the integration variables, an additional integration over the "ends" $ \omega _ {1} $ | ||
| + | and $ \omega _ {2} $ | ||
| + | or over other parameters appearing in (2), differentiation with respect to these parameters, etc.) are commonly called Feynman path integrals. | ||
| − | The representation (2) was introduced by R.P. Feynman [[#References|[1]]] in connection with the new interpretation of quantum mechanics that he proposed. He considered the case when | + | The representation (2) was introduced by R.P. Feynman [[#References|[1]]] in connection with the new interpretation of quantum mechanics that he proposed. He considered the case when $ \Omega = \mathbf R ^ {n} $, |
| + | $ n = 1, 2 \dots $ | ||
| + | the operator $ H $ | ||
| + | has the form $ H = iL $, | ||
| + | where $ L $ | ||
| + | is a Sturm–Liouville differential operator $ Lu = - a \Delta u + Vu $, | ||
| + | $ \Delta $ | ||
| + | is the Laplace operator in $ \mathbf R ^ {n} $, | ||
| + | $ V $ | ||
| + | is some function defined on $ \mathbf R ^ {n} $( | ||
| + | a potential) and $ a > 0 $. | ||
| + | Here one obtains $ W = V $ | ||
| + | in the representation (2) for the function $ G ( x _ {1} , x _ {2} , t) $, | ||
| + | $ x _ {1} , x _ {2} \in \mathbf R ^ {n} $, | ||
| + | $ t > 0 $, | ||
| + | and the complex pre-measure $ \mu _ {x _ {1} , x _ {2} , t } $( | ||
| + | the [[Feynman measure|Feynman measure]]) is given on cylindrical sets of the form | ||
| − | + | $$ | |
| + | \{ {x ( \tau ) } : { | ||
| + | x ( 0) = x _ {1} ,\ | ||
| + | x ( t) = x _ {2} ,\ | ||
| + | x ( \tau _ {i} ) \in G _ {i} ,\ | ||
| + | i = 1 \dots k } \} | ||
| + | $$ | ||
where | where | ||
| − | < | + | $$ |
| + | 0 < \tau _ {1} < \dots < \tau _ {k} < t,\ \ | ||
| + | G _ {i} \subset \mathbf R ^ {n} , | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | i = 1 \dots k,\ k = 1, 2 \dots | ||
| + | $$ | ||
| + | |||
| + | by integration over the set $ G _ {1} \times \dots \times G _ {k} \subseteq ( \mathbf R ^ {n} ) ^ {k} $( | ||
| + | with respect to the usual Lebesgue measure on $ ( \mathbf R ^ {n} ) ^ {k} $) | ||
| + | of the density | ||
| − | + | $$ | |
| + | \prod _ {j = 1 } ^ { {k } + 1 } | ||
| + | [ 2 \pi ia ( \tau _ {j} - | ||
| + | \tau _ {j - 1 } ) ] ^ {-} n/2 \ | ||
| + | \mathop{\rm exp} \left \{ - | ||
| − | + | \frac{( \xi _ {j} - \xi _ {j - 1 } ) ^ {2} }{2ai ( \tau _ {j} - \tau _ {j - 1 } ) } | |
| − | + | \right \} , | |
| + | $$ | ||
| − | where | + | where $ \xi _ {0} = x _ {1} $, |
| + | $ \xi _ {k + 1 } = x _ {2} $, | ||
| + | $ \tau _ {0} = 0 $, | ||
| + | $ \tau _ {k + 1 } = t $. | ||
| + | The expression (2) was regarded by Feynman as the limit of the finitely-multiple integrals obtained by replacing the integral $ \int _ {0} ^ {t} W [ \omega ( t)] d \tau $ | ||
| + | in the exponent in the integrand by some integral sum of it. But he did not give a rigorous foundation for the validity of this definition of the integral, or of equation (2). | ||
| − | Subsequently M. Kac [[#References|[2]]] obtained (2), in which | + | Subsequently M. Kac [[#References|[2]]] obtained (2), in which $ \mu _ {x _ {1} , x _ {2} , t } $ |
| + | is the same as the [[Wiener measure|Wiener measure]], with complete mathematical rigour in the case of an operator $ H = - L $, | ||
| + | where $ L $ | ||
| + | has the form above. Therefore (2) is often called the Feynman–Kac formula. | ||
The Feynman path integral is used as a convenient and deep analytical tool in a variety of questions in mathematical physics ([[#References|[3]]], [[#References|[4]]], [[#References|[6]]]), probability theory [[#References|[7]]] and the theory of differential equations [[#References|[5]]]. | The Feynman path integral is used as a convenient and deep analytical tool in a variety of questions in mathematical physics ([[#References|[3]]], [[#References|[4]]], [[#References|[6]]]), probability theory [[#References|[7]]] and the theory of differential equations [[#References|[5]]]. | ||
| Line 35: | Line 131: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> R.P. Feynman, "Space-time approach to non-relativistic quantum mechanics" ''Rev. Modern Phys.'' , '''20''' (1948) pp. 367–387</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M. Kac, "On some connections between probability theory and differential and integral equations" , ''Proc. 2nd Berkeley Symp. Math. Stat. Probab. (1950)'' , Univ. California Press (1951) pp. 189–215</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Ginibre, "Some applications of functional integration in statistical mechanics" C.M. DeWitt (ed.) R. Stora (ed.) , ''Statistical mechanics and quantum field theory'' , Gordon & Breach pp. 327–427</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> B. Simon, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038470/f03847054.png" /> Euclidean (quantum) field theory" , Princeton Univ. Press (1974)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> Yu.L. Daletskii, "Integration in function spaces" ''Progress in Mathematics'' , '''4''' (1969) pp. 87–132 ''Itogi Nauk. Mat. Anal. 1966'' (1967) pp. 83–124</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> S.A. Albeverio, R.J. Høegh-Krohn, "Mathematical theory of Feynman path integrals" , Springer (1976)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "The theory of stochastic processes" , '''3''' , Springer (1979) (Translated from Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> V.A. Golubeva, "Some problems in the analytic theory of Feynman integrals" ''Russian Math. Surveys'' , '''31''' : 2 (1976) pp. 135–202 ''Uspekhi Mat. Nauk'' , '''31''' : 2 (1976) pp. 135–202</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> R.P. Feynman, "Space-time approach to non-relativistic quantum mechanics" ''Rev. Modern Phys.'' , '''20''' (1948) pp. 367–387</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M. Kac, "On some connections between probability theory and differential and integral equations" , ''Proc. 2nd Berkeley Symp. Math. Stat. Probab. (1950)'' , Univ. California Press (1951) pp. 189–215</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Ginibre, "Some applications of functional integration in statistical mechanics" C.M. DeWitt (ed.) R. Stora (ed.) , ''Statistical mechanics and quantum field theory'' , Gordon & Breach pp. 327–427</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> B. Simon, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038470/f03847054.png" /> Euclidean (quantum) field theory" , Princeton Univ. Press (1974)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> Yu.L. Daletskii, "Integration in function spaces" ''Progress in Mathematics'' , '''4''' (1969) pp. 87–132 ''Itogi Nauk. Mat. Anal. 1966'' (1967) pp. 83–124</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> S.A. Albeverio, R.J. Høegh-Krohn, "Mathematical theory of Feynman path integrals" , Springer (1976)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "The theory of stochastic processes" , '''3''' , Springer (1979) (Translated from Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> V.A. Golubeva, "Some problems in the analytic theory of Feynman integrals" ''Russian Math. Surveys'' , '''31''' : 2 (1976) pp. 135–202 ''Uspekhi Mat. Nauk'' , '''31''' : 2 (1976) pp. 135–202</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Revision as of 19:39, 5 June 2020
Feynman path integral
A collective name for representations in the form of a path integral, or integral over trajectories, of the transition functions (Green functions) of some evolution process.
Suppose that one is given an equation
$$ \tag{1 } \frac{du }{dt } = Hu, $$
where $ 0 \leq t \leq T $, $ T > 0 $, and $ u ( t, \omega ) $ is a function defined on $ T \times \Omega $, where $ \Omega \ni \omega $ is some space and $ H $ is a linear operator acting in a suitable way on a selected space of functions on $ \Omega $. In a number of cases the transition function $ G ( \omega _ {1} , \omega _ {2} , t) $ of equation (1) (that is, the kernel operator of the semi-group $ \mathop{\rm exp} \{ tH \} $, $ t \geq 0 $) can be represented in the form of a path integral
$$ \tag{2 } G ( \omega _ {1} , \omega _ {2} , t) = \ \int\limits _ {\begin{array}{c} \omega : \\ \omega ( 0) = \omega _ {1} \\ \omega ( t) = \omega _ {2} \end{array} } \mathop{\rm exp} \left \{ \int\limits _ { 0 } ^ { t } W [ \omega ( \tau )] d \tau \right \} \mu _ {\omega _ {1} , \omega _ {2} , t } ( d \omega ), $$
where $ W ( \cdot ) $ is some function defined on $ \Omega $, the integration is carried out over the set of "trajectories" $ \omega ( \tau ) $, $ 0 \leq \tau \leq t $, with values in $ \Omega $, "leaving" $ \omega _ {1} $ at time zero and "arriving" at $ \omega _ {2} $ at time $ t $, and, finally, $ \mu _ {\omega _ {1} , \omega _ {2} , t } $ is some measure (or pre-measure) given on this set of trajectories. The integral is interpreted either in the usual Lebesgue sense or in the sense prescribed by any one of the methods of path integration (see [5], [6]). Integrals of the form (2), and also integrals obtained from them by means of certain natural transformations (for example, changing the integration variables, an additional integration over the "ends" $ \omega _ {1} $ and $ \omega _ {2} $ or over other parameters appearing in (2), differentiation with respect to these parameters, etc.) are commonly called Feynman path integrals.
The representation (2) was introduced by R.P. Feynman [1] in connection with the new interpretation of quantum mechanics that he proposed. He considered the case when $ \Omega = \mathbf R ^ {n} $, $ n = 1, 2 \dots $ the operator $ H $ has the form $ H = iL $, where $ L $ is a Sturm–Liouville differential operator $ Lu = - a \Delta u + Vu $, $ \Delta $ is the Laplace operator in $ \mathbf R ^ {n} $, $ V $ is some function defined on $ \mathbf R ^ {n} $( a potential) and $ a > 0 $. Here one obtains $ W = V $ in the representation (2) for the function $ G ( x _ {1} , x _ {2} , t) $, $ x _ {1} , x _ {2} \in \mathbf R ^ {n} $, $ t > 0 $, and the complex pre-measure $ \mu _ {x _ {1} , x _ {2} , t } $( the Feynman measure) is given on cylindrical sets of the form
$$ \{ {x ( \tau ) } : { x ( 0) = x _ {1} ,\ x ( t) = x _ {2} ,\ x ( \tau _ {i} ) \in G _ {i} ,\ i = 1 \dots k } \} $$
where
$$ 0 < \tau _ {1} < \dots < \tau _ {k} < t,\ \ G _ {i} \subset \mathbf R ^ {n} , $$
$$ i = 1 \dots k,\ k = 1, 2 \dots $$
by integration over the set $ G _ {1} \times \dots \times G _ {k} \subseteq ( \mathbf R ^ {n} ) ^ {k} $( with respect to the usual Lebesgue measure on $ ( \mathbf R ^ {n} ) ^ {k} $) of the density
$$ \prod _ {j = 1 } ^ { {k } + 1 } [ 2 \pi ia ( \tau _ {j} - \tau _ {j - 1 } ) ] ^ {-} n/2 \ \mathop{\rm exp} \left \{ - \frac{( \xi _ {j} - \xi _ {j - 1 } ) ^ {2} }{2ai ( \tau _ {j} - \tau _ {j - 1 } ) } \right \} , $$
where $ \xi _ {0} = x _ {1} $, $ \xi _ {k + 1 } = x _ {2} $, $ \tau _ {0} = 0 $, $ \tau _ {k + 1 } = t $. The expression (2) was regarded by Feynman as the limit of the finitely-multiple integrals obtained by replacing the integral $ \int _ {0} ^ {t} W [ \omega ( t)] d \tau $ in the exponent in the integrand by some integral sum of it. But he did not give a rigorous foundation for the validity of this definition of the integral, or of equation (2).
Subsequently M. Kac [2] obtained (2), in which $ \mu _ {x _ {1} , x _ {2} , t } $ is the same as the Wiener measure, with complete mathematical rigour in the case of an operator $ H = - L $, where $ L $ has the form above. Therefore (2) is often called the Feynman–Kac formula.
The Feynman path integral is used as a convenient and deep analytical tool in a variety of questions in mathematical physics ([3], [4], [6]), probability theory [7] and the theory of differential equations [5].
References
| [1] | R.P. Feynman, "Space-time approach to non-relativistic quantum mechanics" Rev. Modern Phys. , 20 (1948) pp. 367–387 |
| [2] | M. Kac, "On some connections between probability theory and differential and integral equations" , Proc. 2nd Berkeley Symp. Math. Stat. Probab. (1950) , Univ. California Press (1951) pp. 189–215 |
| [3] | J. Ginibre, "Some applications of functional integration in statistical mechanics" C.M. DeWitt (ed.) R. Stora (ed.) , Statistical mechanics and quantum field theory , Gordon & Breach pp. 327–427 |
| [4] | B. Simon, "The 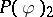 Euclidean (quantum) field theory" , Princeton Univ. Press (1974) Euclidean (quantum) field theory" , Princeton Univ. Press (1974) |
| [5] | Yu.L. Daletskii, "Integration in function spaces" Progress in Mathematics , 4 (1969) pp. 87–132 Itogi Nauk. Mat. Anal. 1966 (1967) pp. 83–124 |
| [6] | S.A. Albeverio, R.J. Høegh-Krohn, "Mathematical theory of Feynman path integrals" , Springer (1976) |
| [7] | I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "The theory of stochastic processes" , 3 , Springer (1979) (Translated from Russian) |
| [8] | V.A. Golubeva, "Some problems in the analytic theory of Feynman integrals" Russian Math. Surveys , 31 : 2 (1976) pp. 135–202 Uspekhi Mat. Nauk , 31 : 2 (1976) pp. 135–202 |
Comments
The phrase "Feynman integral" is also used in physics to denote an (ordinary) integral over a closed loop in a Feynman diagram (arising in particle physics when calculating radiative conditions). Instead of Feynman path integral and Feynman integral one also finds the phrases path integral, functional integral and (rarely) continual integral in the literature.
References
| [a1] | R.P. Feynman, A.R. Hibbs, "Quantum mechanics and path integrals" , McGraw-Hill (1965) |
| [a2] | L.S. Schulman, "Techniques and applications of path integration" , Wiley (1981) |
| [a3] | J. Glimm, A. Jaffe, "Quantum physics, a functional integral point of view" , Springer (1981) |
| [a4] | V.N. Popov, "Functional integrals in quantum field theory and statistical physics" , Reidel (1983) (Translated from Russian) |
| [a5] | J.-P. Antoine (ed.) E. Tirapegui (ed.) , Functional integration. Theory and applications , Plenum (1980) |
| [a6] | B. Simon, "Functional integration and quantum physics" , Acad. Press (1979) pp. 4–6 |
Feynman integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Feynman_integral&oldid=46915