Difference between revisions of "Degenerate series of representations"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | d0308701.png | ||
| + | $#A+1 = 35 n = 2 | ||
| + | $#C+1 = 35 : ~/encyclopedia/old_files/data/D030/D.0300870 Degenerate series of representations | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | The set of representations of a semi-simple Lie group $ G $ | ||
| + | induced by the characters of a non-minimal parabolic subgroup $ P $ | ||
| + | of it. Let $ \Pi $ | ||
| + | be a fundamental root system with respect to which the Lie algebra of a Borel subgroup $ B \subset G $ | ||
| + | is spanned by the root vectors $ e _ \alpha $, | ||
| + | $ \alpha < 0 $. | ||
| + | The set of all parabolic subgroups containing $ B $ | ||
| + | is in one-to-one correspondence with the set of all subsystems $ \Pi _ {0} \subset \Pi $; | ||
| + | $ P \neq B $ | ||
| + | if $ \Pi _ {0} $ | ||
| + | is non-empty, and the Lie algebra of the group $ P $ | ||
| + | is generated by the $ e _ \alpha $, | ||
| + | $ \alpha < 0 $, | ||
| + | and $ e _ \alpha $, | ||
| + | $ \alpha \in \Pi _ {0} $. | ||
| + | Let $ \pi ( \chi ) $ | ||
| + | be the representation of the group $ G $ | ||
| + | induced by a character $ \chi $ | ||
| + | of $ P $ | ||
| + | in the class $ C ^ \infty ( G) $. | ||
| + | There exist characters $ \chi $ | ||
| + | for which $ \pi ( \chi ) $ | ||
| + | can be extended to a unitary representation of the group $ G $ | ||
| + | in $ L _ {2} ( Z) $, | ||
| + | where $ Z $ | ||
| + | is a subgroup in $ G $ | ||
| + | whose Lie algebra is spanned by the vectors $ e _ \alpha $, | ||
| + | $ \alpha > 0 $, | ||
| + | $ \alpha \notin \Delta _ {0} $; | ||
| + | here $ \Delta _ {0} $ | ||
| + | is the additive hull of $ \Pi _ {0} $. | ||
| + | Such representations are known as the representations of the basic degenerate series of representations. A supplementary degenerate series of representations is obtained by extending $ \pi ( \chi ) $( | ||
| + | for certain values of $ \chi $) | ||
| + | with respect to other scalar products in $ \pi ( \chi ) $. | ||
| + | The representations of a degenerate series of representations are irreducible for the group $ G = \mathop{\rm SL} ( n, \mathbf C ) $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.M. Gel'fand, M.A. Naimark, "Unitäre Darstellungen der klassischen Gruppen" , Akademie Verlag (1957) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> K.I. Gross, "The dual of a parabolic subgroup and a degenerate principal series of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d030/d030870/d03087036.png" />" ''Amer. J. Math.'' , '''93''' : 2 (1971) pp. 398–428</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.M. Gel'fand, M.A. Naimark, "Unitäre Darstellungen der klassischen Gruppen" , Akademie Verlag (1957) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> K.I. Gross, "The dual of a parabolic subgroup and a degenerate principal series of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d030/d030870/d03087036.png" />" ''Amer. J. Math.'' , '''93''' : 2 (1971) pp. 398–428</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> B. Speh, D.A., jr. Vogan, "Reducibility of general principal series representations" ''Acta Math.'' , '''145''' (1980) pp. 227–299</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> D.A., jr. Vogan, "The unitary dual of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d030/d030870/d03087037.png" /> over an archimedean field" ''Invent. Math.'' , '''83''' (1986) pp. 449–505</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> B. Speh, D.A., jr. Vogan, "Reducibility of general principal series representations" ''Acta Math.'' , '''145''' (1980) pp. 227–299</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> D.A., jr. Vogan, "The unitary dual of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/d/d030/d030870/d03087037.png" /> over an archimedean field" ''Invent. Math.'' , '''83''' (1986) pp. 449–505</TD></TR></table> | ||
Revision as of 17:32, 5 June 2020
The set of representations of a semi-simple Lie group $ G $
induced by the characters of a non-minimal parabolic subgroup $ P $
of it. Let $ \Pi $
be a fundamental root system with respect to which the Lie algebra of a Borel subgroup $ B \subset G $
is spanned by the root vectors $ e _ \alpha $,
$ \alpha < 0 $.
The set of all parabolic subgroups containing $ B $
is in one-to-one correspondence with the set of all subsystems $ \Pi _ {0} \subset \Pi $;
$ P \neq B $
if $ \Pi _ {0} $
is non-empty, and the Lie algebra of the group $ P $
is generated by the $ e _ \alpha $,
$ \alpha < 0 $,
and $ e _ \alpha $,
$ \alpha \in \Pi _ {0} $.
Let $ \pi ( \chi ) $
be the representation of the group $ G $
induced by a character $ \chi $
of $ P $
in the class $ C ^ \infty ( G) $.
There exist characters $ \chi $
for which $ \pi ( \chi ) $
can be extended to a unitary representation of the group $ G $
in $ L _ {2} ( Z) $,
where $ Z $
is a subgroup in $ G $
whose Lie algebra is spanned by the vectors $ e _ \alpha $,
$ \alpha > 0 $,
$ \alpha \notin \Delta _ {0} $;
here $ \Delta _ {0} $
is the additive hull of $ \Pi _ {0} $.
Such representations are known as the representations of the basic degenerate series of representations. A supplementary degenerate series of representations is obtained by extending $ \pi ( \chi ) $(
for certain values of $ \chi $)
with respect to other scalar products in $ \pi ( \chi ) $.
The representations of a degenerate series of representations are irreducible for the group $ G = \mathop{\rm SL} ( n, \mathbf C ) $.
References
| [1] | I.M. Gel'fand, M.A. Naimark, "Unitäre Darstellungen der klassischen Gruppen" , Akademie Verlag (1957) (Translated from Russian) |
| [2] | K.I. Gross, "The dual of a parabolic subgroup and a degenerate principal series of 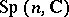 " Amer. J. Math. , 93 : 2 (1971) pp. 398–428 " Amer. J. Math. , 93 : 2 (1971) pp. 398–428 |
Comments
References
| [a1] | B. Speh, D.A., jr. Vogan, "Reducibility of general principal series representations" Acta Math. , 145 (1980) pp. 227–299 |
| [a2] | D.A., jr. Vogan, "The unitary dual of 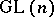 over an archimedean field" Invent. Math. , 83 (1986) pp. 449–505 over an archimedean field" Invent. Math. , 83 (1986) pp. 449–505 |
Degenerate series of representations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Degenerate_series_of_representations&oldid=46616