Difference between revisions of "Darboux sum"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | d0301601.png | ||
| + | $#A+1 = 95 n = 0 | ||
| + | $#C+1 = 95 : ~/encyclopedia/old_files/data/D030/D.0300160 Darboux sum | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| + | |||
| + | A sum of special type. Let a real function $ f $ | ||
| + | be defined and bounded on a segment $ [ a , b ] $, | ||
| + | let $ \tau = {\{ x _ {i} \} } _ {i=} 0 ^ {k} $ | ||
| + | be a decomposition of $ [ a , b ] $: | ||
| + | |||
| + | $$ | ||
| + | a = x _ {0} < x _ {1} < \dots < x _ {k} = b , | ||
| + | $$ | ||
and set | and set | ||
| − | + | $$ | |
| + | m _ {i} = \ | ||
| + | \inf _ {x _ {i-} 1 \leq x \leq x _ {i} } f( x),\ \ | ||
| + | M _ {i} = \sup _ {x _ {i-} 1 \leq x \leq x _ {i} } f ( x) , | ||
| + | $$ | ||
| − | + | $$ | |
| + | \Delta x _ {i} = x _ {i} - x _ {i-} 1 ,\ i = 1 \dots k . | ||
| + | $$ | ||
The sums | The sums | ||
| − | + | $$ | |
| + | s _ \tau = \sum _ {i = 1 } ^ { k } m _ {i} \Delta x _ {i} \ | ||
| + | \textrm{ and } \ \ | ||
| + | S _ \tau = \sum _ {i = 1 } ^ { k } M _ {i} \Delta x _ {i} $$ | ||
| − | are known, respectively, as the lower and upper Darboux sums. For any two decompositions | + | are known, respectively, as the lower and upper Darboux sums. For any two decompositions $ \tau $ |
| + | and $ \tau ^ \prime $ | ||
| + | of $ [ a , b ] $ | ||
| + | the inequality $ s _ \tau \leq S _ {\tau ^ \prime } $ | ||
| + | is valid, i.e. any lower Darboux sum is no larger than an upper. If | ||
| − | + | $$ | |
| + | \sigma _ \tau = \sum _ {i = 1 } ^ { k } f ( \xi _ {i} ) \Delta x _ {i} , | ||
| + | \ \xi _ {i} \in [ x _ {i-} 1 , x _ {i} ] , | ||
| + | $$ | ||
is a Riemann sum, then | is a Riemann sum, then | ||
| − | + | $$ | |
| + | s _ \tau = \inf _ {\xi _ {1} \dots \xi _ {k} } \sigma _ \tau ,\ S _ \tau = \sup _ {\xi _ {1} \dots \xi _ {k} } \sigma _ \tau . | ||
| + | $$ | ||
| − | The geometric meaning of the lower and upper Darboux sums is that they are equal to the planar areas of stepped figures consisting of rectangles whose base widths are | + | The geometric meaning of the lower and upper Darboux sums is that they are equal to the planar areas of stepped figures consisting of rectangles whose base widths are $ \Delta x _ {i} $ |
| + | and with respective heights $ m _ {i} $ | ||
| + | and $ M _ {i} $( | ||
| + | see Fig.) if $ f \geq 0 $. | ||
| + | These figures approximate, from the inside and outside, the curvilinear trapezium formed by the graph of $ f $, | ||
| + | the abscissa axis and the rectilinear segments $ x = a $ | ||
| + | and $ x= b $( | ||
| + | which may degenerate into points). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/d030160a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/d030160a.gif" /> | ||
| Line 29: | Line 71: | ||
The numbers | The numbers | ||
| − | + | $$ \tag{1 } | |
| + | I _ {*} = \sup _ \tau s _ \tau ,\ \ | ||
| + | I ^ {*} = \inf _ \tau S _ \tau $$ | ||
| − | are called, respectively, the lower and the upper Darboux integrals of | + | are called, respectively, the lower and the upper Darboux integrals of $ f $. |
| + | They are the limits of the lower and the upper Darboux sums: | ||
| − | + | $$ | |
| + | I _ {*} = \lim\limits _ {\delta _ \tau \rightarrow 0 } s _ \tau ,\ \ | ||
| + | I ^ {*} = \lim\limits _ {\delta _ \tau \rightarrow 0 } S _ \tau , | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | \delta _ \tau = \max _ {i = 1 \dots k } \Delta x _ {i} $$ | ||
| − | is the fineness (mesh) of the decomposition | + | is the fineness (mesh) of the decomposition $ \tau $. |
| + | The condition | ||
| − | + | $$ \tag{2 } | |
| + | I _ {*} = I ^ {*} | ||
| + | $$ | ||
| − | is necessary and sufficient for a function | + | is necessary and sufficient for a function $ f $ |
| + | to be Riemann integrable on the segment $ [ a , b ] $. | ||
| + | Here, if condition (2) is met, the value of the lower and the upper Darboux integrals becomes identical with the Riemann integral | ||
| − | + | $$ | |
| + | \int\limits _ { a } ^ { b } f ( x) dx . | ||
| + | $$ | ||
| − | With the aid of Darboux sums, condition (2) may be formulated in the following equivalent form: For each | + | With the aid of Darboux sums, condition (2) may be formulated in the following equivalent form: For each $ \epsilon > 0 $ |
| + | there exists a decomposition $ \tau $ | ||
| + | such that | ||
| − | + | $$ | |
| + | S _ \tau - s _ \tau < \epsilon . | ||
| + | $$ | ||
The condition | The condition | ||
| − | + | $$ | |
| + | \lim\limits _ {\delta _ \tau \rightarrow 0 } ( S _ \tau - s _ \tau ) = 0 | ||
| + | $$ | ||
| − | is also necessary and sufficient for the Riemann integrability of | + | is also necessary and sufficient for the Riemann integrability of $ f $ |
| + | on $ [ a , b ] $. | ||
| + | Here | ||
| − | + | $$ | |
| + | S _ \tau - s _ \tau = \sum _ {i = 1 } ^ { k } | ||
| + | \omega _ {i} ( f ) \Delta x _ {i} , | ||
| + | $$ | ||
| − | where | + | where $ \omega _ {i} ( f ) $ |
| + | is the oscillation (cf. [[Oscillation of a function|Oscillation of a function]]) of $ f $ | ||
| + | on | ||
| − | + | $$ | |
| + | [ x _ {i-} 1 , x _ {i} ] ,\ i = 1 \dots k . | ||
| + | $$ | ||
| − | The concept of lower and upper Darboux sums may be generalized to the case of functions of several variables which are measurable in the sense of some positive measure | + | The concept of lower and upper Darboux sums may be generalized to the case of functions of several variables which are measurable in the sense of some positive measure $ \mu $. |
| + | Let $ E $ | ||
| + | be a measurable (for example, Jordan or Lebesgue) subset of the $ n $- | ||
| + | dimensional space, $ n = 1 , 2 \dots $ | ||
| + | and suppose $ \mu ( E) $ | ||
| + | is finite. Let $ \tau = \{ E _ {i} \} _ {i=} 1 ^ {k} $ | ||
| + | be a decomposition of $ E $, | ||
| + | i.e. a system of measurable subsets of $ E $ | ||
| + | such that | ||
| − | + | $$ \tag{3 } | |
| + | \cup _ {i= 1 } ^ { k } E _ {i} = E , | ||
| + | $$ | ||
| − | + | $$ \tag{4 } | |
| + | \mu ( E _ {i} \cap E _ {j } ) = 0 \ \textrm{ if } i \neq j . | ||
| + | $$ | ||
| − | Let a function | + | Let a function $ f $ |
| + | be bounded on $ E $ | ||
| + | and let | ||
| − | + | $$ \tag{5 } | |
| + | m _ {i} = \inf _ {x \in E _ {i} } f ( x), | ||
| + | \ M _ {i} = \sup | ||
| + | _ {x \in E _ {i} } f ( x) ,\ i = 1 \dots k . | ||
| + | $$ | ||
The sums | The sums | ||
| − | + | $$ \tag{6 } | |
| + | s _ \tau = \sum _ {i = 1 } ^ { k } m _ {i} \mu ( E _ {i} ) ,\ \ | ||
| + | S _ \tau = \sum _ {i = 1 } ^ { k } M _ {i} \mu ( E _ {i} ) | ||
| + | $$ | ||
| − | are also said to be, respectively, lower and upper Darboux sums. The lower | + | are also said to be, respectively, lower and upper Darboux sums. The lower $ I _ {*} $ |
| + | and the upper $ I ^ {*} $ | ||
| + | integrals are defined by formulas (1). For Jordan measure, their equality is a sufficient and necessary condition for the function to be Riemann integrable, and their common value coincides with the Riemann integral. For Lebesgue measure, on the other hand, the equality | ||
| − | + | $$ | |
| + | I _ {*} = I ^ {*} = \int\limits _ { E } f( x) dx. | ||
| + | $$ | ||
is always valid for bounded Lebesgue-measurable functions. | is always valid for bounded Lebesgue-measurable functions. | ||
| − | In general, if | + | In general, if $ \mu $ |
| + | is a complete $ \sigma $- | ||
| + | additive bounded measure, defined on a $ \sigma $- | ||
| + | algebra $ \mathfrak S _ \mu $, | ||
| + | if $ f $ | ||
| + | is a bounded measurable real-valued function on $ E $, | ||
| + | if $ \tau = \{ E _ {i} \} _ {i= 1 } ^ {k} $ | ||
| + | is a decomposition of a set $ E \in \mathfrak S _ \mu $ | ||
| + | into $ \mu $- | ||
| + | measurable sets $ E _ {i} $ | ||
| + | which satisfy the conditions (3) and (4), and if the Darboux sums $ s _ \tau $ | ||
| + | and $ S _ \tau $ | ||
| + | are defined by formulas (5) and (6), while the integrals $ I _ {*} $ | ||
| + | and $ I ^ {*} $ | ||
| + | are defined by the formulas (1), in which $ \mu $ | ||
| + | is always understood to mean the measure under consideration, then | ||
| − | + | $$ | |
| + | I _ {*} = I ^ {*} = \int\limits _ { E } f( x) d \mu . | ||
| + | $$ | ||
| − | A generalization of the Darboux sums to unbounded | + | A generalization of the Darboux sums to unbounded $ \mu $- |
| + | measurable functions $ f $ | ||
| + | defined on sets $ E \in \mathfrak S _ \mu $ | ||
| + | are the series (if they are absolutely convergent) | ||
| − | + | $$ \tag{7 } | |
| + | s _ \tau = \sum _ { i= } 1 ^ \infty m _ {i} \mu ( E _ {i} ) ,\ \ | ||
| + | S _ \tau = \sum _ { i= } 1 ^ \infty M _ {i} \mu ( E _ {i} ) | ||
| + | $$ | ||
| − | where | + | where $ \tau = \{ E _ {i} \} _ {i=} 1 ^ \infty $ |
| + | is a decomposition of $ E \in \mathfrak S _ \mu $( | ||
| + | this decomposition consists, generally speaking, of an infinite number of $ \mu $- | ||
| + | measurable sets $ E _ {i} $ | ||
| + | which satisfy condition (4) and are, of course, such that $ \cup _ {i=} 1 ^ \infty E _ {i} = E $), | ||
| + | while $ m _ {i} $ | ||
| + | and $ M _ {i} $ | ||
| + | are defined by (5). In (7) (as in (6) above) it is assumed that $ \infty \cdot 0 = 0 \cdot \infty = 0 $. | ||
| + | If $ I _ {*} $ | ||
| + | and $ I ^ {*} $ | ||
| + | are again defined according to (1) and $ s _ \tau $ | ||
| + | and $ S _ \tau $ | ||
| + | are now defined in the sense of (7) and exist for each $ \tau $, | ||
| + | then $ I _ {*} = I ^ {*} $. | ||
| + | If the value $ I = I _ {*} = I ^ {*} $ | ||
| + | is finite, then $ f $ | ||
| + | is integrable with respect to $ \mu $ | ||
| + | and $ I = \int _ {E} f ( x) d \mu $. | ||
Named after G. Darboux [[#References|[1]]]. | Named after G. Darboux [[#References|[1]]]. | ||
Revision as of 17:32, 5 June 2020
A sum of special type. Let a real function $ f $
be defined and bounded on a segment $ [ a , b ] $,
let $ \tau = {\{ x _ {i} \} } _ {i=} 0 ^ {k} $
be a decomposition of $ [ a , b ] $:
$$ a = x _ {0} < x _ {1} < \dots < x _ {k} = b , $$
and set
$$ m _ {i} = \ \inf _ {x _ {i-} 1 \leq x \leq x _ {i} } f( x),\ \ M _ {i} = \sup _ {x _ {i-} 1 \leq x \leq x _ {i} } f ( x) , $$
$$ \Delta x _ {i} = x _ {i} - x _ {i-} 1 ,\ i = 1 \dots k . $$
The sums
$$ s _ \tau = \sum _ {i = 1 } ^ { k } m _ {i} \Delta x _ {i} \ \textrm{ and } \ \ S _ \tau = \sum _ {i = 1 } ^ { k } M _ {i} \Delta x _ {i} $$
are known, respectively, as the lower and upper Darboux sums. For any two decompositions $ \tau $ and $ \tau ^ \prime $ of $ [ a , b ] $ the inequality $ s _ \tau \leq S _ {\tau ^ \prime } $ is valid, i.e. any lower Darboux sum is no larger than an upper. If
$$ \sigma _ \tau = \sum _ {i = 1 } ^ { k } f ( \xi _ {i} ) \Delta x _ {i} , \ \xi _ {i} \in [ x _ {i-} 1 , x _ {i} ] , $$
is a Riemann sum, then
$$ s _ \tau = \inf _ {\xi _ {1} \dots \xi _ {k} } \sigma _ \tau ,\ S _ \tau = \sup _ {\xi _ {1} \dots \xi _ {k} } \sigma _ \tau . $$
The geometric meaning of the lower and upper Darboux sums is that they are equal to the planar areas of stepped figures consisting of rectangles whose base widths are $ \Delta x _ {i} $ and with respective heights $ m _ {i} $ and $ M _ {i} $( see Fig.) if $ f \geq 0 $. These figures approximate, from the inside and outside, the curvilinear trapezium formed by the graph of $ f $, the abscissa axis and the rectilinear segments $ x = a $ and $ x= b $( which may degenerate into points).
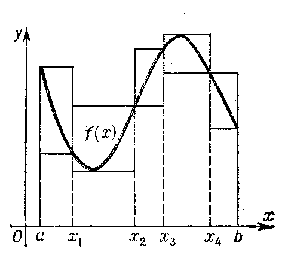
Figure: d030160a
The numbers
$$ \tag{1 } I _ {*} = \sup _ \tau s _ \tau ,\ \ I ^ {*} = \inf _ \tau S _ \tau $$
are called, respectively, the lower and the upper Darboux integrals of $ f $. They are the limits of the lower and the upper Darboux sums:
$$ I _ {*} = \lim\limits _ {\delta _ \tau \rightarrow 0 } s _ \tau ,\ \ I ^ {*} = \lim\limits _ {\delta _ \tau \rightarrow 0 } S _ \tau , $$
where
$$ \delta _ \tau = \max _ {i = 1 \dots k } \Delta x _ {i} $$
is the fineness (mesh) of the decomposition $ \tau $. The condition
$$ \tag{2 } I _ {*} = I ^ {*} $$
is necessary and sufficient for a function $ f $ to be Riemann integrable on the segment $ [ a , b ] $. Here, if condition (2) is met, the value of the lower and the upper Darboux integrals becomes identical with the Riemann integral
$$ \int\limits _ { a } ^ { b } f ( x) dx . $$
With the aid of Darboux sums, condition (2) may be formulated in the following equivalent form: For each $ \epsilon > 0 $ there exists a decomposition $ \tau $ such that
$$ S _ \tau - s _ \tau < \epsilon . $$
The condition
$$ \lim\limits _ {\delta _ \tau \rightarrow 0 } ( S _ \tau - s _ \tau ) = 0 $$
is also necessary and sufficient for the Riemann integrability of $ f $ on $ [ a , b ] $. Here
$$ S _ \tau - s _ \tau = \sum _ {i = 1 } ^ { k } \omega _ {i} ( f ) \Delta x _ {i} , $$
where $ \omega _ {i} ( f ) $ is the oscillation (cf. Oscillation of a function) of $ f $ on
$$ [ x _ {i-} 1 , x _ {i} ] ,\ i = 1 \dots k . $$
The concept of lower and upper Darboux sums may be generalized to the case of functions of several variables which are measurable in the sense of some positive measure $ \mu $. Let $ E $ be a measurable (for example, Jordan or Lebesgue) subset of the $ n $- dimensional space, $ n = 1 , 2 \dots $ and suppose $ \mu ( E) $ is finite. Let $ \tau = \{ E _ {i} \} _ {i=} 1 ^ {k} $ be a decomposition of $ E $, i.e. a system of measurable subsets of $ E $ such that
$$ \tag{3 } \cup _ {i= 1 } ^ { k } E _ {i} = E , $$
$$ \tag{4 } \mu ( E _ {i} \cap E _ {j } ) = 0 \ \textrm{ if } i \neq j . $$
Let a function $ f $ be bounded on $ E $ and let
$$ \tag{5 } m _ {i} = \inf _ {x \in E _ {i} } f ( x), \ M _ {i} = \sup _ {x \in E _ {i} } f ( x) ,\ i = 1 \dots k . $$
The sums
$$ \tag{6 } s _ \tau = \sum _ {i = 1 } ^ { k } m _ {i} \mu ( E _ {i} ) ,\ \ S _ \tau = \sum _ {i = 1 } ^ { k } M _ {i} \mu ( E _ {i} ) $$
are also said to be, respectively, lower and upper Darboux sums. The lower $ I _ {*} $ and the upper $ I ^ {*} $ integrals are defined by formulas (1). For Jordan measure, their equality is a sufficient and necessary condition for the function to be Riemann integrable, and their common value coincides with the Riemann integral. For Lebesgue measure, on the other hand, the equality
$$ I _ {*} = I ^ {*} = \int\limits _ { E } f( x) dx. $$
is always valid for bounded Lebesgue-measurable functions.
In general, if $ \mu $ is a complete $ \sigma $- additive bounded measure, defined on a $ \sigma $- algebra $ \mathfrak S _ \mu $, if $ f $ is a bounded measurable real-valued function on $ E $, if $ \tau = \{ E _ {i} \} _ {i= 1 } ^ {k} $ is a decomposition of a set $ E \in \mathfrak S _ \mu $ into $ \mu $- measurable sets $ E _ {i} $ which satisfy the conditions (3) and (4), and if the Darboux sums $ s _ \tau $ and $ S _ \tau $ are defined by formulas (5) and (6), while the integrals $ I _ {*} $ and $ I ^ {*} $ are defined by the formulas (1), in which $ \mu $ is always understood to mean the measure under consideration, then
$$ I _ {*} = I ^ {*} = \int\limits _ { E } f( x) d \mu . $$
A generalization of the Darboux sums to unbounded $ \mu $- measurable functions $ f $ defined on sets $ E \in \mathfrak S _ \mu $ are the series (if they are absolutely convergent)
$$ \tag{7 } s _ \tau = \sum _ { i= } 1 ^ \infty m _ {i} \mu ( E _ {i} ) ,\ \ S _ \tau = \sum _ { i= } 1 ^ \infty M _ {i} \mu ( E _ {i} ) $$
where $ \tau = \{ E _ {i} \} _ {i=} 1 ^ \infty $ is a decomposition of $ E \in \mathfrak S _ \mu $( this decomposition consists, generally speaking, of an infinite number of $ \mu $- measurable sets $ E _ {i} $ which satisfy condition (4) and are, of course, such that $ \cup _ {i=} 1 ^ \infty E _ {i} = E $), while $ m _ {i} $ and $ M _ {i} $ are defined by (5). In (7) (as in (6) above) it is assumed that $ \infty \cdot 0 = 0 \cdot \infty = 0 $. If $ I _ {*} $ and $ I ^ {*} $ are again defined according to (1) and $ s _ \tau $ and $ S _ \tau $ are now defined in the sense of (7) and exist for each $ \tau $, then $ I _ {*} = I ^ {*} $. If the value $ I = I _ {*} = I ^ {*} $ is finite, then $ f $ is integrable with respect to $ \mu $ and $ I = \int _ {E} f ( x) d \mu $.
Named after G. Darboux [1].
References
| [1] | G. Darboux, Ann. Sci. Ecole Norm. Sup. Ser. 2 , 4 (1875) pp. 57–112 |
| [2] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian) |
| [3] | L.D. Kudryavtsev, "Mathematical analysis" , 1–2 , Moscow (1973) (In Russian) |
| [4] | S.M. Nikol'skii, "A course of mathematical analysis" , 1–2 , MIR (1977) (Translated from Russian) |
Darboux sum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Darboux_sum&oldid=46580