Difference between revisions of "Critical point"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | c0270901.png | ||
| + | $#A+1 = 92 n = 3 | ||
| + | $#C+1 = 92 : ~/encyclopedia/old_files/data/C027/C.0207090 Critical point | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | For an analytic function $ f ( z) $, | |
| + | a critical point of order $ m $ | ||
| + | is a point $ a $ | ||
| + | of the complex plane at which $ f ( z) $ | ||
| + | is regular but its derivative $ f ^ { \prime } ( z) $ | ||
| + | has a zero of order $ m $, | ||
| + | where $ m $ | ||
| + | is a natural number. In other words, a critical point is defined by the conditions | ||
| − | + | $$ | |
| + | \lim\limits _ {z \rightarrow a } | ||
| + | |||
| + | \frac{f ( z) - f ( a) }{( z - a) ^ {m} } | ||
| + | = 0,\ \ | ||
| + | \lim\limits _ {z \rightarrow a } | ||
| + | |||
| + | \frac{f ( z) - f ( a) }{( z - a) ^ {m+} 1 } | ||
| + | \neq 0. | ||
| + | $$ | ||
| − | + | A critical point at infinity, $ a = \infty $, | |
| + | of order $ m $, | ||
| + | for a function $ f ( z) $ | ||
| + | which is regular at infinity, is defined by the conditions | ||
| − | + | $$ | |
| + | \lim\limits _ {z \rightarrow \infty } | ||
| + | [ f ( z) - f ( \infty )] | ||
| + | z ^ {m} = 0,\ \ | ||
| + | \lim\limits _ {z \rightarrow \infty } | ||
| + | [ f ( z) - f ( \infty )] | ||
| + | z ^ {m + 1 } \neq 0. | ||
| + | $$ | ||
| − | + | Under the analytic mapping $ w = f ( z) $, | |
| + | the angle between two curves emanating from a critical point of order $ m $ | ||
| + | is increased by a factor $ m + 1 $. | ||
| + | If $ f ( z) $ | ||
| + | is regarded as the complex potential of some planar flow of an incompressible liquid, a critical point is characterized by the property that through it pass not one but $ m + 1 $ | ||
| + | stream lines, and the velocity of the flow at a critical point vanishes. In terms of the inverse function $ z = \psi ( w) $( | ||
| + | i.e. the function for which $ f [ \psi ( w)] \equiv w $), | ||
| + | a critical point is an algebraic branch point of order $ m + 1 $. | ||
| − | the latter being defined in a neighbourhood | + | A point $ a $ |
| + | of a complex $ ( n - m) $- | ||
| + | dimensional irreducible analytic set | ||
| + | |||
| + | $$ | ||
| + | M = \ | ||
| + | \{ {z \in V } : { | ||
| + | f _ {1} ( z) = \dots = | ||
| + | f _ {m} ( z) = 0 } \} | ||
| + | , | ||
| + | $$ | ||
| + | |||
| + | the latter being defined in a neighbourhood $ V $ | ||
| + | of $ a $ | ||
| + | in the complex space $ \mathbf C ^ {n} $ | ||
| + | by the conditions $ f _ {1} ( z) = \dots = f _ {m} ( z) = 0 $, | ||
| + | where $ f _ {1} \dots f _ {m} $ | ||
| + | are holomorphic functions on $ V $ | ||
| + | in $ n $ | ||
| + | complex variables, $ z = ( z _ {1} \dots z _ {n} ) $, | ||
| + | is called a critical point if the rank of the Jacobian matrix $ \| \partial f _ {j} / \partial z _ {k} \| $, | ||
| + | $ j = 1 \dots m $, | ||
| + | $ k = 1 \dots n $, | ||
| + | is less than $ m $. | ||
| + | The other points of $ M $ | ||
| + | are called regular. There are relatively few critical points on $ M $: | ||
| + | They form an analytic set of complex dimension at most $ n - m - 1 $. | ||
| + | In particular, when $ m = 1 $, | ||
| + | i.e. if $ M = \{ f _ {1} ( z) = 0 \} $, | ||
| + | and the dimension of $ M $ | ||
| + | is $ n - 1 $, | ||
| + | the dimension of the set of critical points is at most $ n - 2 $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , '''1''' , Springer (1964) {{MR|0173749}} {{ZBL|0135.12101}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B.V. Shabat, "Introduction of complex analysis" , '''1–2''' , Moscow (1976) (In Russian) {{MR|}} {{ZBL|0799.32001}} {{ZBL|0732.32001}} {{ZBL|0732.30001}} {{ZBL|0578.32001}} {{ZBL|0574.30001}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , '''1''' , Springer (1964) {{MR|0173749}} {{ZBL|0135.12101}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B.V. Shabat, "Introduction of complex analysis" , '''1–2''' , Moscow (1976) (In Russian) {{MR|}} {{ZBL|0799.32001}} {{ZBL|0732.32001}} {{ZBL|0732.30001}} {{ZBL|0578.32001}} {{ZBL|0574.30001}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | A point as described under 2) is also called a singular point of | + | A point as described under 2) is also called a singular point of $ M $, |
| + | cf. [[#References|[a1]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Grauert, K. Fritzsche, "Several complex variables" , Springer (1976) pp. 95 (Translated from German) {{MR|0414912}} {{ZBL|0381.32001}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Grauert, K. Fritzsche, "Several complex variables" , Springer (1976) pp. 95 (Translated from German) {{MR|0414912}} {{ZBL|0381.32001}} </TD></TR></table> | ||
| − | A critical point of a smooth (i.e. continuously differentiable) mapping | + | A critical point of a smooth (i.e. continuously differentiable) mapping $ f $ |
| + | of a $ k $- | ||
| + | dimensional differentiable manifold $ M $ | ||
| + | into an $ l $- | ||
| + | dimensional differentiable manifold $ N $ | ||
| + | is a point $ x _ {0} \in M $ | ||
| + | such that the rank $ \mathop{\rm Rk} _ {x _ {0} } f $ | ||
| + | of $ f $ | ||
| + | at this point (i.e. the dimension of the image $ df ( T _ {x _ {0} } M) $ | ||
| + | of the tangent space to $ M $ | ||
| + | under the differential mapping $ df: T _ {x _ {0} } M \rightarrow T _ {f ( x _ {0} ) } N $) | ||
| + | is less than $ l $. | ||
| + | The set of all critical points is called the critical set, the image $ f( x _ {0} ) $ | ||
| + | of a critical point $ x _ {0} $ | ||
| + | is called a critical value, and a point $ y \in N $ | ||
| + | which is not the image of any critical point is called a regular point or a regular value (though it need not belong to the image $ f( M) $); | ||
| + | non-critical points of $ M $ | ||
| + | are also called regular. | ||
| − | According to Sard's theorem, if | + | According to Sard's theorem, if $ f $ |
| + | is smooth of class $ C ^ {m} $, | ||
| + | $ m > \min ( k - l, 0) $, | ||
| + | then the image of the critical set is of the first category in $ N $( | ||
| + | i.e. it is the union of at most countably many nowhere-dense sets) and has $ l $- | ||
| + | dimensional measure zero (see [[#References|[1]]], [[#References|[2]]]). The lower bound for $ m $ | ||
| + | cannot be weakened (see [[#References|[3]]]). The case most frequently needed is $ m = \infty $( | ||
| + | in which case the proof is simplified, see [[#References|[4]]]). This theorem is widely used for reductions to [[General position|general position]] via "small movements" ; for example, it may readily be used to prove that, given two smooth submanifolds in $ \mathbf R ^ {n} $, | ||
| + | there exists an arbitrarily small translation of one of them such that their intersection will also be a submanifold (see [[#References|[2]]], [[#References|[4]]], and also [[Transversality|Transversality]] of mappings). | ||
| − | According to the above definition, when < | + | According to the above definition, when $ k < l $ |
| + | every point $ x _ {0} \in M $ | ||
| + | must be considered as critical. Then, however, there are considerable differences between the properties of the points $ x _ {0} $ | ||
| + | for which $ \mathop{\rm Rk} _ {x _ {0} } f = k $ | ||
| + | and the points for which $ \mathop{\rm Rk} _ {x _ {0} } f < k $. | ||
| + | In the former case there is a neighbourhood of $ x _ {0} $ | ||
| + | in which the mapping $ f $ | ||
| + | looks roughly like the standard imbedding of $ \mathbf R ^ {k} $ | ||
| + | into $ \mathbf R ^ {l} $; | ||
| + | more precisely, there exist local coordinates $ x _ {1} \dots x _ {k} $ | ||
| + | near $ x _ {0} $( | ||
| + | on $ M $) | ||
| + | and $ y _ {1} \dots y _ {l} $ | ||
| + | near $ f ( x _ {0} ) $( | ||
| + | on $ N $), | ||
| + | in terms of which $ f $ | ||
| + | is given by | ||
| − | + | $$ | |
| + | y _ {i} = x _ {i} ,\ \ | ||
| + | i \leq k; \ \ | ||
| + | y _ {k + 1 } = \dots | ||
| + | = y _ {l} = 0. | ||
| + | $$ | ||
| − | In the second case the image of a neighbourhood of | + | In the second case the image of a neighbourhood of $ x _ {0} $ |
| + | need not be a manifold, displaying instead various singularities — cusps, self-intersections, etc. For this reason, the definition of a critical point is often modified to include only points $ x _ {0} $ | ||
| + | such that $ \mathop{\rm Rk} _ {x _ {0} } f < \min ( k, l) $; | ||
| + | corresponding modifications are then necessary in the definitions of the other terms listed above [[#References|[5]]]. | ||
| − | The behaviour of mappings in a neighbourhood of a critical point is investigated in the theory of singularities of differentiable mappings (see [[#References|[5]]], [[#References|[6]]]). In that context one studies not arbitrary critical points (concerning which little can be said), but critical points satisfying conditions which ensure that they are "not too strongly degenerate" and "typical" . Thus, one considers critical points of sufficiently smooth mappings, or families of mappings (which depend smoothly on finitely many parameters), which are "unremovable" in the sense that, under small perturbations ( "small" being understood in the sense of | + | The behaviour of mappings in a neighbourhood of a critical point is investigated in the theory of singularities of differentiable mappings (see [[#References|[5]]], [[#References|[6]]]). In that context one studies not arbitrary critical points (concerning which little can be said), but critical points satisfying conditions which ensure that they are "not too strongly degenerate" and "typical" . Thus, one considers critical points of sufficiently smooth mappings, or families of mappings (which depend smoothly on finitely many parameters), which are "unremovable" in the sense that, under small perturbations ( "small" being understood in the sense of $ C ^ {m} $ |
| + | for suitable $ m $) | ||
| + | of the original mapping, or of the original family, the perturbed mapping (family) has a critical point of the same type in some neighbourhood of the original critical point. For a mapping $ M \rightarrow \mathbf R $( | ||
| + | i.e. an ordinary scalar function; in this case critical points are often called stationary points), critical points which are typical in the indicated sense are the non-degenerate critical points at which the Hessian is a non-degenerate quadratic form. Concerning typical critical points for a family of functions see [[#References|[6]]], [[#References|[7]]]. | ||
====References==== | ====References==== | ||
Revision as of 17:31, 5 June 2020
For an analytic function $ f ( z) $,
a critical point of order $ m $
is a point $ a $
of the complex plane at which $ f ( z) $
is regular but its derivative $ f ^ { \prime } ( z) $
has a zero of order $ m $,
where $ m $
is a natural number. In other words, a critical point is defined by the conditions
$$ \lim\limits _ {z \rightarrow a } \frac{f ( z) - f ( a) }{( z - a) ^ {m} } = 0,\ \ \lim\limits _ {z \rightarrow a } \frac{f ( z) - f ( a) }{( z - a) ^ {m+} 1 } \neq 0. $$
A critical point at infinity, $ a = \infty $, of order $ m $, for a function $ f ( z) $ which is regular at infinity, is defined by the conditions
$$ \lim\limits _ {z \rightarrow \infty } [ f ( z) - f ( \infty )] z ^ {m} = 0,\ \ \lim\limits _ {z \rightarrow \infty } [ f ( z) - f ( \infty )] z ^ {m + 1 } \neq 0. $$
Under the analytic mapping $ w = f ( z) $, the angle between two curves emanating from a critical point of order $ m $ is increased by a factor $ m + 1 $. If $ f ( z) $ is regarded as the complex potential of some planar flow of an incompressible liquid, a critical point is characterized by the property that through it pass not one but $ m + 1 $ stream lines, and the velocity of the flow at a critical point vanishes. In terms of the inverse function $ z = \psi ( w) $( i.e. the function for which $ f [ \psi ( w)] \equiv w $), a critical point is an algebraic branch point of order $ m + 1 $.
A point $ a $ of a complex $ ( n - m) $- dimensional irreducible analytic set
$$ M = \ \{ {z \in V } : { f _ {1} ( z) = \dots = f _ {m} ( z) = 0 } \} , $$
the latter being defined in a neighbourhood $ V $ of $ a $ in the complex space $ \mathbf C ^ {n} $ by the conditions $ f _ {1} ( z) = \dots = f _ {m} ( z) = 0 $, where $ f _ {1} \dots f _ {m} $ are holomorphic functions on $ V $ in $ n $ complex variables, $ z = ( z _ {1} \dots z _ {n} ) $, is called a critical point if the rank of the Jacobian matrix $ \| \partial f _ {j} / \partial z _ {k} \| $, $ j = 1 \dots m $, $ k = 1 \dots n $, is less than $ m $. The other points of $ M $ are called regular. There are relatively few critical points on $ M $: They form an analytic set of complex dimension at most $ n - m - 1 $. In particular, when $ m = 1 $, i.e. if $ M = \{ f _ {1} ( z) = 0 \} $, and the dimension of $ M $ is $ n - 1 $, the dimension of the set of critical points is at most $ n - 2 $.
References
| [1] | A. Hurwitz, R. Courant, "Vorlesungen über allgemeine Funktionentheorie und elliptische Funktionen" , 1 , Springer (1964) MR0173749 Zbl 0135.12101 |
| [2] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) Zbl 0799.32001 Zbl 0732.32001 Zbl 0732.30001 Zbl 0578.32001 Zbl 0574.30001 |
Comments
A point as described under 2) is also called a singular point of $ M $, cf. [a1].
References
| [a1] | H. Grauert, K. Fritzsche, "Several complex variables" , Springer (1976) pp. 95 (Translated from German) MR0414912 Zbl 0381.32001 |
A critical point of a smooth (i.e. continuously differentiable) mapping $ f $ of a $ k $- dimensional differentiable manifold $ M $ into an $ l $- dimensional differentiable manifold $ N $ is a point $ x _ {0} \in M $ such that the rank $ \mathop{\rm Rk} _ {x _ {0} } f $ of $ f $ at this point (i.e. the dimension of the image $ df ( T _ {x _ {0} } M) $ of the tangent space to $ M $ under the differential mapping $ df: T _ {x _ {0} } M \rightarrow T _ {f ( x _ {0} ) } N $) is less than $ l $. The set of all critical points is called the critical set, the image $ f( x _ {0} ) $ of a critical point $ x _ {0} $ is called a critical value, and a point $ y \in N $ which is not the image of any critical point is called a regular point or a regular value (though it need not belong to the image $ f( M) $); non-critical points of $ M $ are also called regular.
According to Sard's theorem, if $ f $ is smooth of class $ C ^ {m} $, $ m > \min ( k - l, 0) $, then the image of the critical set is of the first category in $ N $( i.e. it is the union of at most countably many nowhere-dense sets) and has $ l $- dimensional measure zero (see [1], [2]). The lower bound for $ m $ cannot be weakened (see [3]). The case most frequently needed is $ m = \infty $( in which case the proof is simplified, see [4]). This theorem is widely used for reductions to general position via "small movements" ; for example, it may readily be used to prove that, given two smooth submanifolds in $ \mathbf R ^ {n} $, there exists an arbitrarily small translation of one of them such that their intersection will also be a submanifold (see [2], [4], and also Transversality of mappings).
According to the above definition, when $ k < l $ every point $ x _ {0} \in M $ must be considered as critical. Then, however, there are considerable differences between the properties of the points $ x _ {0} $ for which $ \mathop{\rm Rk} _ {x _ {0} } f = k $ and the points for which $ \mathop{\rm Rk} _ {x _ {0} } f < k $. In the former case there is a neighbourhood of $ x _ {0} $ in which the mapping $ f $ looks roughly like the standard imbedding of $ \mathbf R ^ {k} $ into $ \mathbf R ^ {l} $; more precisely, there exist local coordinates $ x _ {1} \dots x _ {k} $ near $ x _ {0} $( on $ M $) and $ y _ {1} \dots y _ {l} $ near $ f ( x _ {0} ) $( on $ N $), in terms of which $ f $ is given by
$$ y _ {i} = x _ {i} ,\ \ i \leq k; \ \ y _ {k + 1 } = \dots = y _ {l} = 0. $$
In the second case the image of a neighbourhood of $ x _ {0} $ need not be a manifold, displaying instead various singularities — cusps, self-intersections, etc. For this reason, the definition of a critical point is often modified to include only points $ x _ {0} $ such that $ \mathop{\rm Rk} _ {x _ {0} } f < \min ( k, l) $; corresponding modifications are then necessary in the definitions of the other terms listed above [5].
The behaviour of mappings in a neighbourhood of a critical point is investigated in the theory of singularities of differentiable mappings (see [5], [6]). In that context one studies not arbitrary critical points (concerning which little can be said), but critical points satisfying conditions which ensure that they are "not too strongly degenerate" and "typical" . Thus, one considers critical points of sufficiently smooth mappings, or families of mappings (which depend smoothly on finitely many parameters), which are "unremovable" in the sense that, under small perturbations ( "small" being understood in the sense of $ C ^ {m} $ for suitable $ m $) of the original mapping, or of the original family, the perturbed mapping (family) has a critical point of the same type in some neighbourhood of the original critical point. For a mapping $ M \rightarrow \mathbf R $( i.e. an ordinary scalar function; in this case critical points are often called stationary points), critical points which are typical in the indicated sense are the non-degenerate critical points at which the Hessian is a non-degenerate quadratic form. Concerning typical critical points for a family of functions see [6], [7].
References
| [1] | A. Sard, "The measure of critical values of differentiable maps" Bull. Amer. Math Soc. , 48 (1942) pp. 883–890 MR7523 Zbl 0063.06720 |
| [2] | S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964) MR0193578 Zbl 0129.13102 |
| [3] | H. Whitney, "A function not constant on a connected set of critical points" Duke Math. J. , 1 : 4 (1935) pp. 514–517 MR1545896 Zbl 0013.05801 Zbl 61.1117.01 Zbl 61.0262.07 |
| [4] | J.W. Milnor, "Topology from the differential viewpoint" , Univ. Virginia Press (1965) |
| [5] | M. Golubitsky, "Stable mappings and their singularities" , Springer (1974) MR0467801 MR0341518 Zbl 0434.58001 Zbl 0429.58004 Zbl 0294.58004 |
| [6] | P. Bröcker, L. Lander, "Differentiable germs and catastrophes" , Cambridge Univ. Press (1975) MR0494220 Zbl 0302.58006 |
| [7] | V.I. Arnol'd, "Normal forms of functions near degenerate critical points, the Weyl groups 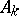 , , 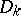 , , 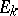 and Lagrangian singularities" Funktsional. Anal. i Prilozh. , 6 : 4 (1972) pp. 3–25 (In Russian) and Lagrangian singularities" Funktsional. Anal. i Prilozh. , 6 : 4 (1972) pp. 3–25 (In Russian) |
D.V. Anosov
Critical point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Critical_point&oldid=46555