Difference between revisions of "Correlation property for sequences"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | c1104302.png | ||
| + | $#A+1 = 82 n = 2 | ||
| + | $#C+1 = 82 : ~/encyclopedia/old_files/data/C110/C.1100430 Correlation property for sequences | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | Complex-valued $ n $- | |
| + | periodic sequences (i.e. sequences $ a = ( a _ {i} ) _ {i = 0 } ^ \infty $ | ||
| + | with $ a _ {i + n } = a _ {i} $, | ||
| + | $ a _ {i} \in \mathbf C $) | ||
| + | with "good" correlation properties have many applications in signal processing (spread spectrum and code division multiple access communication systems, see [[#References|[a10]]]). A good survey is [[#References|[a9]]]. Periodic sequences are recurring or shift register sequences, see [[#References|[a2]]]. | ||
| − | + | If $ a $ | |
| + | and $ b $ | ||
| + | are $ n $- | ||
| + | periodic sequences, one defines $ C _ {a,b } ( t ) = \sum _ {i = 0 } ^ {n - 1 } a _ {i} { {b _ {i + t } } bar } $. | ||
| + | These numbers are called the periodic correlation coefficients (in case $ a = b $, | ||
| + | periodic autocorrelation coefficients). Sometimes also the aperiodic correlation $ A _ {a,b } ( t ) = \sum _ {i = 0 } ^ {n - 1 - t } a _ {i} { {b _ {i + t } } bar } $ | ||
| + | is of interest. The odd correlation of $ ( a _ {i} ) $ | ||
| + | and $ ( b _ {i} ) $ | ||
| + | is $ O _ {a,b } ( t ) = A _ {x,y } ( t ) - A _ {x,y } ( t - n ) $, | ||
| + | $ t = 1 \dots n $. | ||
| − | + | The goal is the design of large sets $ {\mathcal S} = \{ a ^ {( 1 ) } \dots a ^ {( m ) } \} $ | |
| + | of $ n $- | ||
| + | periodic sequences such that | ||
| − | ( | + | $$ |
| + | m ( {\mathcal S} ) = \max \left \{ { \left | {C _ {a ^ {( i ) } ,b ^ {( j ) } } ( t ) } \right | } :\right . | ||
| + | $$ | ||
| − | + | $$ | |
| + | \left . | ||
| + | {t = 0 \dots n - 1, i,j = 1 \dots s, t \neq 0 \textrm{ if } i = j } \right \} | ||
| + | $$ | ||
| − | + | (or the respective value for the aperiodic correlation) is small. Sequences with $ C _ {a,a } ( t ) = 0 $, | |
| + | $ t = 1 \dots n - 1 $, | ||
| + | are called perfect. Perfect sequences whose entries are $ t $ | ||
| + | th roots of unity ( $ t > 2 $) | ||
| + | are known for many periods $ n $, | ||
| + | but no example of a $ \pm 1 $- | ||
| + | sequence with period $ n > 4 $ | ||
| + | is known (the perfect sequence conjecture: there are no perfect binary sequences with $ n > 4 $). | ||
| + | In the aperiodic case, the $ \pm 1 $- | ||
| + | sequences with odd period $ n $ | ||
| + | and aperiodic correlation coefficients $ 0 $ | ||
| + | and $ \pm 1 $( | ||
| + | Barker sequences) have been classified [[#References|[a12]]]. If $ n $ | ||
| + | is even, the existence of an $ n $- | ||
| + | periodic Barker sequence implies the existence of an $ n $- | ||
| + | periodic perfect $ \pm 1 $- | ||
| + | sequence. | ||
| − | + | If one assumes that the sequences are normalized, i.e. $ C _ {a ^ {( i ) } ,a ^ {( i ) } } = n $, | |
| + | then it is known that for $ k \geq 0 $, | ||
| − | + | $$ | |
| + | m ( {\mathcal S} ) ^ {2k } \geq { | ||
| + | \frac{1}{nm ( nm - 1 ) } | ||
| + | } \left \{ { | ||
| + | \frac{n ^ {2k } ( nm ) ^ {2} }{\left ( \begin{array}{c} | ||
| + | {k + n - 1 } \\ | ||
| + | {n - 1 } | ||
| + | \end{array} | ||
| + | \right ) } | ||
| + | } - mn ^ {2k + 1 } \right \} | ||
| + | $$ | ||
| − | + | and, if the entries of the sequences are just $ \pm 1 $: | |
| − | + | $$ | |
| + | m ( {\mathcal S} ) ^ {2} > ( 2k + 1 ) ( n - k ) + { | ||
| + | \frac{k ( k + 1 ) }{2} | ||
| + | } - { | ||
| + | \frac{2 ^ {k} n ^ {2k + 1 } }{m ( 2k ) ! \left ( \begin{array}{c} | ||
| + | n \\ | ||
| + | k | ||
| + | \end{array} | ||
| + | \right ) } | ||
| + | } | ||
| + | $$ | ||
| − | + | for $ 0 \leq k < { {2n } / 5 } $. | |
| + | If the entries of the sequences are $ t $ | ||
| + | th roots of unity ( $ t > 2 $), | ||
| + | then the bound is | ||
| − | + | $$ | |
| + | m ( {\mathcal S} ) > { | ||
| + | \frac{k + 1 }{2} | ||
| + | } ( 2n - k ) - { | ||
| + | \frac{2 ^ {k} n ^ {2k + 1 } }{m ( k! ) ^ {2} \left ( \begin{array}{c} | ||
| + | {2n } \\ | ||
| + | k | ||
| + | \end{array} | ||
| + | \right ) } | ||
| + | } , k \geq 0. | ||
| + | $$ | ||
| − | In | + | The first bound is due to L.R. Welch, the second two bounds are due to V.M. Sidel'nikov. In all cases, $ k $ |
| + | is an integer. Some improvements of these bounds are known. Similar bounds hold for the maximum odd correlation coefficient [[#References|[a7]]]. | ||
| + | |||
| + | Important classes of sequences are derived from so-called $ m $- | ||
| + | sequences $ ( a _ {i} ) = ( { \mathop{\rm trace} } ( \alpha ^ {i} ) ) $, | ||
| + | where $ \alpha $ | ||
| + | is a primitive element of the [[Finite field|finite field]] $ { \mathop{\rm GF} } ( q ^ {e} ) $ | ||
| + | and $ { \mathop{\rm trace} } ( x ) = \sum _ {i = 0 } ^ {e - 1 } x ^ {q ^ {i} } $. | ||
| + | The sequence $ ( a _ {i} ) $ | ||
| + | is defined over a finite field. The complex-valued sequences corresponding to such finite field sequences are $ ( \chi ( a _ {i} ) ) $, | ||
| + | where $ \chi $ | ||
| + | is a [[Homomorphism|homomorphism]] from the additive group of the field into the multiplicative group of $ \mathbf C $. | ||
| + | The $ m $- | ||
| + | sequences yield complex sequences with autocorrelation coefficients $ - 1 $. | ||
| + | The $ s $- | ||
| + | decimation of an $ n $- | ||
| + | periodic sequence is $ a _ {s \cdot i ( { \mathop{\rm mod} } n ) } $. | ||
| + | Systematic investigations of the correlation properties between $ m $- | ||
| + | sequences and their decimations can be found in [[#References|[a4]]] and [[#References|[a11]]]. The $ m $- | ||
| + | sequences are recurring sequences of maximum period length. Their good autocorrelation properties show that they have good "random" properties (pseudo-noise sequences). | ||
| + | |||
| + | In many cases, variations of the construction of $ m $- | ||
| + | sequences yield sets of sequences with optimal correlation properties with respect to the Welch and Sidel'nikov bounds: The cases $ m \approx n $ | ||
| + | and $ m \approx \sqrt n $ | ||
| + | have been investigated intensively. Regarding binary sequences, both the Gold sequences ( $ m = n + 2 = 2 ^ {e} + 1 $) | ||
| + | and the Kasami sequences ( $ m = \sqrt {n + 1 } = 2 ^ {e/2 } $) | ||
| + | are asymptotically optimal. (One says that a family $ {\mathcal S} _ {n} $ | ||
| + | of sets of $ n $- | ||
| + | periodic sequences is asymptotically optimal if $ {\lim\limits } _ {n \rightarrow \infty } { {m ( {\mathcal S} _ {n} ) } / {\sqrt n } } = b $, | ||
| + | is best possible. If $ | { {\mathcal S} _ {n} } | \approx n $, | ||
| + | the lower bounds show that $ b \geq \sqrt 2 $ | ||
| + | for binary and $ b \geq 1 $ | ||
| + | for arbitrary complex valued sequences. For $ | { {\mathcal S} _ {n} } | \approx \sqrt n $, | ||
| + | one has $ b \geq 1 $.) | ||
| + | Sequences whose entries are $ t $ | ||
| + | th roots of unity ( $ t \neq 2 $) | ||
| + | and which are optimal have been constructed ( $ m \approx n $, | ||
| + | $ t $ | ||
| + | prime [[#References|[a5]]]; $ m \approx n $, | ||
| + | $ t = 4 $[[#References|[a1]]]). The latter construction is of particular interest in view of its connection with Kerdock and Preparata codes (cf. [[Kerdock and Preparata codes|Kerdock and Preparata codes]]) and their linearity as codes over $ \mathbf Z _ {4} $, | ||
| + | see [[#References|[a3]]]. More sequences with good correlation properties where $ t $ | ||
| + | is not a prime number can be constructed. In these constructions, sequences over Galois rings instead of finite fields are converted via homomorphisms $ \chi $ | ||
| + | into complex-valued sequences. A systematic investigation of shift register sequences over rings can be found in [[#References|[a6]]]. | ||
Other important classes of sequences with good correlation properties are bent function sequences, [[#References|[a8]]]. | Other important classes of sequences with good correlation properties are bent function sequences, [[#References|[a8]]]. | ||
Revision as of 17:31, 5 June 2020
Complex-valued $ n $-
periodic sequences (i.e. sequences $ a = ( a _ {i} ) _ {i = 0 } ^ \infty $
with $ a _ {i + n } = a _ {i} $,
$ a _ {i} \in \mathbf C $)
with "good" correlation properties have many applications in signal processing (spread spectrum and code division multiple access communication systems, see [a10]). A good survey is [a9]. Periodic sequences are recurring or shift register sequences, see [a2].
If $ a $ and $ b $ are $ n $- periodic sequences, one defines $ C _ {a,b } ( t ) = \sum _ {i = 0 } ^ {n - 1 } a _ {i} { {b _ {i + t } } bar } $. These numbers are called the periodic correlation coefficients (in case $ a = b $, periodic autocorrelation coefficients). Sometimes also the aperiodic correlation $ A _ {a,b } ( t ) = \sum _ {i = 0 } ^ {n - 1 - t } a _ {i} { {b _ {i + t } } bar } $ is of interest. The odd correlation of $ ( a _ {i} ) $ and $ ( b _ {i} ) $ is $ O _ {a,b } ( t ) = A _ {x,y } ( t ) - A _ {x,y } ( t - n ) $, $ t = 1 \dots n $.
The goal is the design of large sets $ {\mathcal S} = \{ a ^ {( 1 ) } \dots a ^ {( m ) } \} $ of $ n $- periodic sequences such that
$$ m ( {\mathcal S} ) = \max \left \{ { \left | {C _ {a ^ {( i ) } ,b ^ {( j ) } } ( t ) } \right | } :\right . $$
$$ \left . {t = 0 \dots n - 1, i,j = 1 \dots s, t \neq 0 \textrm{ if } i = j } \right \} $$
(or the respective value for the aperiodic correlation) is small. Sequences with $ C _ {a,a } ( t ) = 0 $, $ t = 1 \dots n - 1 $, are called perfect. Perfect sequences whose entries are $ t $ th roots of unity ( $ t > 2 $) are known for many periods $ n $, but no example of a $ \pm 1 $- sequence with period $ n > 4 $ is known (the perfect sequence conjecture: there are no perfect binary sequences with $ n > 4 $). In the aperiodic case, the $ \pm 1 $- sequences with odd period $ n $ and aperiodic correlation coefficients $ 0 $ and $ \pm 1 $( Barker sequences) have been classified [a12]. If $ n $ is even, the existence of an $ n $- periodic Barker sequence implies the existence of an $ n $- periodic perfect $ \pm 1 $- sequence.
If one assumes that the sequences are normalized, i.e. $ C _ {a ^ {( i ) } ,a ^ {( i ) } } = n $, then it is known that for $ k \geq 0 $,
$$ m ( {\mathcal S} ) ^ {2k } \geq { \frac{1}{nm ( nm - 1 ) } } \left \{ { \frac{n ^ {2k } ( nm ) ^ {2} }{\left ( \begin{array}{c} {k + n - 1 } \\ {n - 1 } \end{array} \right ) } } - mn ^ {2k + 1 } \right \} $$
and, if the entries of the sequences are just $ \pm 1 $:
$$ m ( {\mathcal S} ) ^ {2} > ( 2k + 1 ) ( n - k ) + { \frac{k ( k + 1 ) }{2} } - { \frac{2 ^ {k} n ^ {2k + 1 } }{m ( 2k ) ! \left ( \begin{array}{c} n \\ k \end{array} \right ) } } $$
for $ 0 \leq k < { {2n } / 5 } $. If the entries of the sequences are $ t $ th roots of unity ( $ t > 2 $), then the bound is
$$ m ( {\mathcal S} ) > { \frac{k + 1 }{2} } ( 2n - k ) - { \frac{2 ^ {k} n ^ {2k + 1 } }{m ( k! ) ^ {2} \left ( \begin{array}{c} {2n } \\ k \end{array} \right ) } } , k \geq 0. $$
The first bound is due to L.R. Welch, the second two bounds are due to V.M. Sidel'nikov. In all cases, $ k $ is an integer. Some improvements of these bounds are known. Similar bounds hold for the maximum odd correlation coefficient [a7].
Important classes of sequences are derived from so-called $ m $- sequences $ ( a _ {i} ) = ( { \mathop{\rm trace} } ( \alpha ^ {i} ) ) $, where $ \alpha $ is a primitive element of the finite field $ { \mathop{\rm GF} } ( q ^ {e} ) $ and $ { \mathop{\rm trace} } ( x ) = \sum _ {i = 0 } ^ {e - 1 } x ^ {q ^ {i} } $. The sequence $ ( a _ {i} ) $ is defined over a finite field. The complex-valued sequences corresponding to such finite field sequences are $ ( \chi ( a _ {i} ) ) $, where $ \chi $ is a homomorphism from the additive group of the field into the multiplicative group of $ \mathbf C $. The $ m $- sequences yield complex sequences with autocorrelation coefficients $ - 1 $. The $ s $- decimation of an $ n $- periodic sequence is $ a _ {s \cdot i ( { \mathop{\rm mod} } n ) } $. Systematic investigations of the correlation properties between $ m $- sequences and their decimations can be found in [a4] and [a11]. The $ m $- sequences are recurring sequences of maximum period length. Their good autocorrelation properties show that they have good "random" properties (pseudo-noise sequences).
In many cases, variations of the construction of $ m $- sequences yield sets of sequences with optimal correlation properties with respect to the Welch and Sidel'nikov bounds: The cases $ m \approx n $ and $ m \approx \sqrt n $ have been investigated intensively. Regarding binary sequences, both the Gold sequences ( $ m = n + 2 = 2 ^ {e} + 1 $) and the Kasami sequences ( $ m = \sqrt {n + 1 } = 2 ^ {e/2 } $) are asymptotically optimal. (One says that a family $ {\mathcal S} _ {n} $ of sets of $ n $- periodic sequences is asymptotically optimal if $ {\lim\limits } _ {n \rightarrow \infty } { {m ( {\mathcal S} _ {n} ) } / {\sqrt n } } = b $, is best possible. If $ | { {\mathcal S} _ {n} } | \approx n $, the lower bounds show that $ b \geq \sqrt 2 $ for binary and $ b \geq 1 $ for arbitrary complex valued sequences. For $ | { {\mathcal S} _ {n} } | \approx \sqrt n $, one has $ b \geq 1 $.) Sequences whose entries are $ t $ th roots of unity ( $ t \neq 2 $) and which are optimal have been constructed ( $ m \approx n $, $ t $ prime [a5]; $ m \approx n $, $ t = 4 $[a1]). The latter construction is of particular interest in view of its connection with Kerdock and Preparata codes (cf. Kerdock and Preparata codes) and their linearity as codes over $ \mathbf Z _ {4} $, see [a3]. More sequences with good correlation properties where $ t $ is not a prime number can be constructed. In these constructions, sequences over Galois rings instead of finite fields are converted via homomorphisms $ \chi $ into complex-valued sequences. A systematic investigation of shift register sequences over rings can be found in [a6].
Other important classes of sequences with good correlation properties are bent function sequences, [a8].
References
| [a1] | S. Boztas, A.R. Hammons, P.V. Kumar, "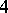 -phase sequence with near optimum correlation properties" IEEE Trans. Inform. Th. , 38 (1992) pp. 1101–1113 -phase sequence with near optimum correlation properties" IEEE Trans. Inform. Th. , 38 (1992) pp. 1101–1113 |
| [a2] | S.W. Golomb, "Shift register sequences" , Aegean Park, Laguna Hills (California) (1982) (Edition: Revised) |
| [a3] | A.R. Hammons, P.V. Kumar, A.R. Calderbank, N.J.A. Sloane, P. Solé, "The 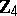 -linearity of Kerdock, Preparata, Goethals, and related codes" IEEE Trans. Information Th. , 40 (1994) pp. 301–319 -linearity of Kerdock, Preparata, Goethals, and related codes" IEEE Trans. Information Th. , 40 (1994) pp. 301–319 |
| [a4] | T. Helleseth, "Some results about the cross-correlation function between two maximal linear sequences" Discrete Math. , 16 (1976) pp. 209–232 |
| [a5] | P.V. Kumar, O. Moreno, "Prime-phase sequences with periodic correlation properties better than binary sequences" IEEE Trans. Information Th. , 37 (1991) pp. 603–616 |
| [a6] | V.L. Kurakin, A.S. Kuzmin, A.V. Mikhalev, A.A. Nechaev, "Linear recurring sequences over rings and modules" J. Math. Sci. , 76 (1995) pp. 2793–2915 |
| [a7] | W.H. Mow, "On the bounds on odd correlation of sequences" IEEE Trans. Information Th. , 40 (1994) pp. 954–955 |
| [a8] | J.D. Olsen, R.A. Scholtz, L.R. Welch, "Bent-function sequences" IEEE Trans. Information Th. , 28 (1982) pp. 858–864 |
| [a9] | D.V. Sarwate, M.B. Pursley, "Crosscorrelation properties of pseudorandom and related sequences" Proc. IEEE , 68 (1980) pp. 593–619 |
| [a10] | M. Simon, J. Omura, R. Scholtz, B. Levitt, "Spread Spectrum Communications" , I , Computer Sci. Press (1985) |
| [a11] | H.M. Trachtenberg, "On the cross-correlation functions of maximal recurring sequences" Ph.D. Thesis, Univ. Southern California (1970) |
| [a12] | R. Turyn, J. Storer, "On binary sequences" Proc. Amer. Math. Soc. , 12 (1961) pp. 394–399 |
Correlation property for sequences. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Correlation_property_for_sequences&oldid=46527