Difference between revisions of "Commutant lifting theorem"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (typo) |
||
| Line 74: | Line 74: | ||
Now, let $ A $ | Now, let $ A $ | ||
be the Hankel operator from $ {\mathcal H} = H ^ {2} $ | be the Hankel operator from $ {\mathcal H} = H ^ {2} $ | ||
| − | into $ {\mathcal H} _ {1} = L ^ {2} \ | + | into $ {\mathcal H} _ {1} = L ^ {2} \ominus H ^ {2} $ |
defined by $ Ax = Pfx $ | defined by $ Ax = Pfx $ | ||
for $ x $ | for $ x $ | ||
Revision as of 16:22, 5 June 2020
Let $ T _ {1} $
be a contraction on a Hilbert space $ {\mathcal H} _ {1} $,
that is, $ \| {T _ {1} } \| \leq 1 $.
Recall that $ U $
is an isometric dilation of $ T _ {1} $
if $ U $
is an isometry (cf. Isometric operator) on a Hilbert space $ {\mathcal K} \supseteq {\mathcal H} _ {1} $
and $ {\mathcal H} _ {1} $
is an invariant subspace for $ U ^ {*} $
satisfying $ U ^ {*} \mid {\mathcal H} _ {1} = T _ {1} ^ {*} $.
The Sz.-Nagy–Shäffer construction shows that all contractions admit an isometric dilation [a1], [a5]. This sets the stage for the following result, known as the Sz.-Nagy–Foias commutant lifting theorem [a1], [a4], [a5].
Let $ U $ on $ {\mathcal K} $ be an isometric dilation for a contraction $ T _ {1} $ on $ {\mathcal H} _ {1} $. Let $ A $ be an operator from the Hilbert space $ {\mathcal H} $ into $ {\mathcal H} _ {1} $ and $ T $ an isometry on $ {\mathcal H} $ satisfying $ T _ {1} A = AT $. Then there exists an operator $ B $ from $ {\mathcal H} $ into $ {\mathcal K} $ satisfying the following three conditions: $ UB = BT $, $ \| B \| = \| A \| $ and $ PB = A $, where $ P $ is the orthogonal projection onto $ {\mathcal H} _ {1} $.
The commutant lifting theorem was inspired by seminal work of D. Sarason [a3] on $ H ^ \infty $ interpolation. It can be used to solve many classical and modern $ H ^ \infty $ interpolation problems, including the Carathéodory, Nevanlinna–Pick, Hermite–Féjer, Nudelman, Nehari, and Löwner interpolation problems in both their classical and tangential form (see [a1] and also Carathéodory interpolation; Nevanlinna–Pick interpolation). The commutant lifting theorem can also be used to solve problems in $ H ^ \infty $ control theory and inverse scattering [a1], [a2].
There is a one-to-one correspondence between the set of all solutions in the commutant lifting theorem and a certain choice sequence of contractions. This choice sequence is a generalization of the Schur numbers used to solve the Carathéodory interpolation problem or the reflection coefficients appearing in inverse scattering problems for layered media in geophysics. There is also a one-to-one correspondence between the sets of all solutions for the commutant lifting theorem and a certain contractive analytic function in the open unit disc. This characterization of all solutions has several different network interpretations [a1].
As an illustration of the commutant lifting theorem, consider the Nehari interpolation problem
$$ d _ \infty = \inf \left \{ {\left \| {f - h } \right \| _ \infty } : {h \in H ^ \infty } \right \} , $$
where $ f $ is a given function in $ L ^ \infty $. Here, $ L ^ \infty $ is the Banach space of all Lebesgue-measurable functions $ g $ on the unit circle whose norm $ \| g \| _ \infty = { \mathop{\rm ess} \sup } \{ {| {g ( e ^ {it } ) } | } : {0 \leq t < 2 \pi } \} $ is finite, and $ H ^ \infty $ is the subspace of $ L ^ \infty $ consisting of all functions $ g $ in $ L ^ \infty $ whose Fourier coefficients at $ e ^ {int } $ are zero for all $ n < 0 $. Likewise, $ L ^ {2} $ is the Hilbert space of all Lebesgue-measurable, square-integrable functions on the unit circle, and $ H ^ {2} $ is the subspace of $ L ^ {2} $ consisting of all functions in $ L ^ {2} $ whose Fourier coefficients at $ e ^ {int } $ vanish for all $ n < 0 $. Now, let $ A $ be the Hankel operator from $ {\mathcal H} = H ^ {2} $ into $ {\mathcal H} _ {1} = L ^ {2} \ominus H ^ {2} $ defined by $ Ax = Pfx $ for $ x $ in $ H ^ {2} $. Let $ T $ be the isometry on $ H ^ {2} $ and $ U $ the unitary operator on $ {\mathcal K} = L ^ {2} $ defined by $ Tx = e ^ {it } x $ and $ Uy = e ^ {it } y $, respectively. Let $ T _ {1} $ be the contraction on $ {\mathcal H} _ {1} $ defined by $ T _ {1} h _ {1} = PUh _ {1} $ for $ h _ {1} $ in $ {\mathcal H} _ {1} $. Since $ T _ {1} ^ {*} = U ^ {*} \mid {\mathcal H} _ {1} $, it follows that $ U $ is an isometric lifting of $ T _ {1} $. By applying the commutant lifting theorem, there exists an operator $ B $ from $ H ^ {2} $ into $ L ^ {2} $ satisfying $ UB = BT $, $ \| B \| = \| A \| $ and $ PB = A $. Therefore, the error $ d _ \infty = \| A \| $, and there exists an $ h \in H ^ \infty $ such that $ d _ \infty = \| {f - h } \| _ \infty $.
References
| [a1] | C. Foias, A.E. Frazho, "The commutant lifting approach to interpolation problems" , Operator Theory: Advances and Applications , 44 , Birkhäuser (1990) |
| [a2] | C. Foias, H. Özbay, A. Tannenbaum, "Robust control of infinite-dimensional systems" , Springer (1996) |
| [a3] | D. Sarason, "Generalized interpolation in 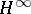 " Trans. Amer. Math. Soc. , 127 (1967) pp. 179–203 " Trans. Amer. Math. Soc. , 127 (1967) pp. 179–203 |
| [a4] | B. Sz.-Nagy, C. Foias, "Dilatation des commutants d'opérateurs" C.R. Acad. Sci. Paris , A266 (1968) pp. 493–495 |
| [a5] | B. Sz.-Nagy, C. Foias, "Harmonic analysis of operators on Hilbert space" , North-Holland (1970) |
Commutant lifting theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Commutant_lifting_theorem&oldid=46511