Difference between revisions of "Confluent hypergeometric equation"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | c0246901.png | ||
| + | $#A+1 = 17 n = 1 | ||
| + | $#C+1 = 17 : ~/encyclopedia/old_files/data/C024/C.0204690 Confluent hypergeometric equation, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''degenerate hypergeometric equation'' | ''degenerate hypergeometric equation'' | ||
The second-order ordinary linear differential equation | The second-order ordinary linear differential equation | ||
| − | + | $$ \tag{1 } | |
| + | zw ^ {\prime\prime} + ( \gamma - z) w ^ \prime - \alpha w = 0,\ \ | ||
| + | \alpha , \gamma = \textrm{ const } , | ||
| + | $$ | ||
or, in self-adjoint form, | or, in self-adjoint form, | ||
| − | + | $$ | |
| + | ( e ^ {- z } z ^ \gamma w ^ \prime ) ^ \prime - | ||
| + | \alpha e ^ {- z } z ^ {\gamma - 1 } w = 0. | ||
| + | $$ | ||
| − | In general, the variables | + | In general, the variables $ z, w $ |
| + | and the parameters $ \alpha , \gamma $ | ||
| + | may assume complex values. The [[Whittaker equation|Whittaker equation]] is a reduced form of equation (1). Equation (1) is closely connected with the [[Hypergeometric equation|hypergeometric equation]]. The confluent hypergeometric equation can be regarded as an equation obtained from the [[Riemann differential equation|Riemann differential equation]] as a result of the merging of two singular points. The point $ x = 0 $ | ||
| + | is a regular singular point for equation (1), while the point $ x = \infty $ | ||
| + | is a strong singular point (cf. [[Singular point|Singular point]]). E.E. Kummer [[#References|[1]]] was the first to undertake a systematic study of the solutions of equation (1). | ||
| − | The solutions of equation (1) are expressed through the [[Confluent hypergeometric function|confluent hypergeometric function]] | + | The solutions of equation (1) are expressed through the [[Confluent hypergeometric function|confluent hypergeometric function]] $ \Phi ( \alpha ; \gamma ; z) $. |
| + | If $ \gamma $ | ||
| + | is not an integer, the general solution of equation (1) may be written in the form | ||
| − | + | $$ \tag{2 } | |
| + | w = C _ {1} \Phi ( \alpha ; \gamma ; z) + | ||
| + | C _ {2} z ^ {1 - \gamma } \Phi ( \alpha + 1 - \gamma ; 2 - \gamma ; z), | ||
| + | $$ | ||
| − | where | + | where $ C _ {1} $ |
| + | and $ C _ {2} $ | ||
| + | are arbitrary constants. This representation is valid in the complex $ z $- | ||
| + | plane with the slit $ ( - \infty , 0) $. | ||
| + | If $ \gamma $ | ||
| + | is an integer, the general solution has a more complicated form (may contain logarithmic terms). Functions other than those in (2) (e.g. [[Whittaker functions|Whittaker functions]] [[#References|[2]]], [[#References|[3]]]) can also be selected as a fundamental system of solutions of equation (1). Solutions of (1) can also be represented by contour integrals in the complex $ z $- | ||
| + | plane. | ||
Many second-order ordinary linear differential equations (e.g. the [[Bessel equation|Bessel equation]]) can be reduced to equation (1) by a transformation of the unknown function and of the independent variable [[#References|[4]]]. In particular, equations of the type | Many second-order ordinary linear differential equations (e.g. the [[Bessel equation|Bessel equation]]) can be reduced to equation (1) by a transformation of the unknown function and of the independent variable [[#References|[4]]]. In particular, equations of the type | ||
| − | + | $$ | |
| + | ( a _ {0} z + b _ {0} ) w ^ {\prime\prime} + | ||
| + | ( a _ {1} z + b _ {1} ) w ^ \prime + | ||
| + | ( a _ {2} z + b _ {2} ) w = 0, | ||
| + | $$ | ||
| − | + | $$ | |
| + | a _ {i} , b _ {i} = \textrm{ const } , | ||
| + | $$ | ||
can be integrated using the confluent hypergeometric function. | can be integrated using the confluent hypergeometric function. | ||
Revision as of 17:46, 4 June 2020
degenerate hypergeometric equation
The second-order ordinary linear differential equation
$$ \tag{1 } zw ^ {\prime\prime} + ( \gamma - z) w ^ \prime - \alpha w = 0,\ \ \alpha , \gamma = \textrm{ const } , $$
or, in self-adjoint form,
$$ ( e ^ {- z } z ^ \gamma w ^ \prime ) ^ \prime - \alpha e ^ {- z } z ^ {\gamma - 1 } w = 0. $$
In general, the variables $ z, w $ and the parameters $ \alpha , \gamma $ may assume complex values. The Whittaker equation is a reduced form of equation (1). Equation (1) is closely connected with the hypergeometric equation. The confluent hypergeometric equation can be regarded as an equation obtained from the Riemann differential equation as a result of the merging of two singular points. The point $ x = 0 $ is a regular singular point for equation (1), while the point $ x = \infty $ is a strong singular point (cf. Singular point). E.E. Kummer [1] was the first to undertake a systematic study of the solutions of equation (1).
The solutions of equation (1) are expressed through the confluent hypergeometric function $ \Phi ( \alpha ; \gamma ; z) $. If $ \gamma $ is not an integer, the general solution of equation (1) may be written in the form
$$ \tag{2 } w = C _ {1} \Phi ( \alpha ; \gamma ; z) + C _ {2} z ^ {1 - \gamma } \Phi ( \alpha + 1 - \gamma ; 2 - \gamma ; z), $$
where $ C _ {1} $ and $ C _ {2} $ are arbitrary constants. This representation is valid in the complex $ z $- plane with the slit $ ( - \infty , 0) $. If $ \gamma $ is an integer, the general solution has a more complicated form (may contain logarithmic terms). Functions other than those in (2) (e.g. Whittaker functions [2], [3]) can also be selected as a fundamental system of solutions of equation (1). Solutions of (1) can also be represented by contour integrals in the complex $ z $- plane.
Many second-order ordinary linear differential equations (e.g. the Bessel equation) can be reduced to equation (1) by a transformation of the unknown function and of the independent variable [4]. In particular, equations of the type
$$ ( a _ {0} z + b _ {0} ) w ^ {\prime\prime} + ( a _ {1} z + b _ {1} ) w ^ \prime + ( a _ {2} z + b _ {2} ) w = 0, $$
$$ a _ {i} , b _ {i} = \textrm{ const } , $$
can be integrated using the confluent hypergeometric function.
References
| [1] | E.E. Kummer, "Ueber die hypergeometrische Reihe 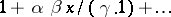 " J. Reine Angew. Math. , 15 (1836) pp. 39–83; 127–172 " J. Reine Angew. Math. , 15 (1836) pp. 39–83; 127–172 |
| [2] | A. Krazer, W. Franz, "Transzendente Funktionen" , Akademie Verlag (1960) |
| [3] | H. Bateman (ed.) A. Erdélyi (ed.) , Higher transcendental functions , 1. The gamma function. The hypergeometric functions. Legendre functions , McGraw-Hill (1953) |
| [4] | E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1971) |
Confluent hypergeometric equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Confluent_hypergeometric_equation&oldid=46449