Difference between revisions of "Commutant lifting theorem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | c1103201.png | ||
| + | $#A+1 = 78 n = 1 | ||
| + | $#C+1 = 78 : ~/encyclopedia/old_files/data/C110/C.1100320 Commutant lifting theorem | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | The commutant lifting theorem was inspired by seminal work of D. Sarason [[#References|[a3]]] on | + | Let $ T _ {1} $ |
| + | be a [[Contraction(2)|contraction]] on a [[Hilbert space|Hilbert space]] $ {\mathcal H} _ {1} $, | ||
| + | that is, $ \| {T _ {1} } \| \leq 1 $. | ||
| + | Recall that $ U $ | ||
| + | is an isometric dilation of $ T _ {1} $ | ||
| + | if $ U $ | ||
| + | is an isometry (cf. [[Isometric operator|Isometric operator]]) on a Hilbert space $ {\mathcal K} \supseteq {\mathcal H} _ {1} $ | ||
| + | and $ {\mathcal H} _ {1} $ | ||
| + | is an invariant subspace for $ U ^ {*} $ | ||
| + | satisfying $ U ^ {*} \mid {\mathcal H} _ {1} = T _ {1} ^ {*} $. | ||
| + | The Sz.-Nagy–Shäffer construction shows that all contractions admit an isometric dilation [[#References|[a1]]], [[#References|[a5]]]. This sets the stage for the following result, known as the Sz.-Nagy–Foias commutant lifting theorem [[#References|[a1]]], [[#References|[a4]]], [[#References|[a5]]]. | ||
| + | |||
| + | Let $ U $ | ||
| + | on $ {\mathcal K} $ | ||
| + | be an isometric dilation for a contraction $ T _ {1} $ | ||
| + | on $ {\mathcal H} _ {1} $. | ||
| + | Let $ A $ | ||
| + | be an operator from the Hilbert space $ {\mathcal H} $ | ||
| + | into $ {\mathcal H} _ {1} $ | ||
| + | and $ T $ | ||
| + | an isometry on $ {\mathcal H} $ | ||
| + | satisfying $ T _ {1} A = AT $. | ||
| + | Then there exists an operator $ B $ | ||
| + | from $ {\mathcal H} $ | ||
| + | into $ {\mathcal K} $ | ||
| + | satisfying the following three conditions: $ UB = BT $, | ||
| + | $ \| B \| = \| A \| $ | ||
| + | and $ PB = A $, | ||
| + | where $ P $ | ||
| + | is the orthogonal projection onto $ {\mathcal H} _ {1} $. | ||
| + | |||
| + | The commutant lifting theorem was inspired by seminal work of D. Sarason [[#References|[a3]]] on $ H ^ \infty $ | ||
| + | interpolation. It can be used to solve many classical and modern $ H ^ \infty $ | ||
| + | interpolation problems, including the Carathéodory, Nevanlinna–Pick, Hermite–Féjer, Nudelman, Nehari, and Löwner interpolation problems in both their classical and tangential form (see [[#References|[a1]]] and also [[Carathéodory interpolation|Carathéodory interpolation]]; [[Nevanlinna–Pick interpolation|Nevanlinna–Pick interpolation]]). The commutant lifting theorem can also be used to solve problems in [[H^infinity-control-theory| $ H ^ \infty $ | ||
| + | control theory]] and inverse scattering [[#References|[a1]]], [[#References|[a2]]]. | ||
There is a one-to-one correspondence between the set of all solutions in the commutant lifting theorem and a certain choice sequence of contractions. This choice sequence is a generalization of the Schur numbers used to solve the Carathéodory interpolation problem or the reflection coefficients appearing in inverse scattering problems for layered media in geophysics. There is also a one-to-one correspondence between the sets of all solutions for the commutant lifting theorem and a certain contractive analytic function in the open unit disc. This characterization of all solutions has several different network interpretations [[#References|[a1]]]. | There is a one-to-one correspondence between the set of all solutions in the commutant lifting theorem and a certain choice sequence of contractions. This choice sequence is a generalization of the Schur numbers used to solve the Carathéodory interpolation problem or the reflection coefficients appearing in inverse scattering problems for layered media in geophysics. There is also a one-to-one correspondence between the sets of all solutions for the commutant lifting theorem and a certain contractive analytic function in the open unit disc. This characterization of all solutions has several different network interpretations [[#References|[a1]]]. | ||
| Line 9: | Line 51: | ||
As an illustration of the commutant lifting theorem, consider the Nehari interpolation problem | As an illustration of the commutant lifting theorem, consider the Nehari interpolation problem | ||
| − | + | $$ | |
| + | d _ \infty = \inf \left \{ {\left \| {f - h } \right \| _ \infty } : {h \in H ^ \infty } \right \} , | ||
| + | $$ | ||
| − | where | + | where $ f $ |
| + | is a given function in $ L ^ \infty $. | ||
| + | Here, $ L ^ \infty $ | ||
| + | is the Banach space of all Lebesgue-measurable functions $ g $ | ||
| + | on the unit circle whose norm $ \| g \| _ \infty = { \mathop{\rm ess} \sup } \{ {| {g ( e ^ {it } ) } | } : {0 \leq t < 2 \pi } \} $ | ||
| + | is finite, and $ H ^ \infty $ | ||
| + | is the subspace of $ L ^ \infty $ | ||
| + | consisting of all functions $ g $ | ||
| + | in $ L ^ \infty $ | ||
| + | whose Fourier coefficients at $ e ^ {int } $ | ||
| + | are zero for all $ n < 0 $. | ||
| + | Likewise, $ L ^ {2} $ | ||
| + | is the Hilbert space of all Lebesgue-measurable, square-integrable functions on the unit circle, and $ H ^ {2} $ | ||
| + | is the subspace of $ L ^ {2} $ | ||
| + | consisting of all functions in $ L ^ {2} $ | ||
| + | whose Fourier coefficients at $ e ^ {int } $ | ||
| + | vanish for all $ n < 0 $. | ||
| + | Now, let $ A $ | ||
| + | be the Hankel operator from $ {\mathcal H} = H ^ {2} $ | ||
| + | into $ {\mathcal H} _ {1} = L ^ {2} \omn H ^ {2} $ | ||
| + | defined by $ Ax = Pfx $ | ||
| + | for $ x $ | ||
| + | in $ H ^ {2} $. | ||
| + | Let $ T $ | ||
| + | be the isometry on $ H ^ {2} $ | ||
| + | and $ U $ | ||
| + | the unitary operator on $ {\mathcal K} = L ^ {2} $ | ||
| + | defined by $ Tx = e ^ {it } x $ | ||
| + | and $ Uy = e ^ {it } y $, | ||
| + | respectively. Let $ T _ {1} $ | ||
| + | be the contraction on $ {\mathcal H} _ {1} $ | ||
| + | defined by $ T _ {1} h _ {1} = PUh _ {1} $ | ||
| + | for $ h _ {1} $ | ||
| + | in $ {\mathcal H} _ {1} $. | ||
| + | Since $ T _ {1} ^ {*} = U ^ {*} \mid {\mathcal H} _ {1} $, | ||
| + | it follows that $ U $ | ||
| + | is an isometric lifting of $ T _ {1} $. | ||
| + | By applying the commutant lifting theorem, there exists an operator $ B $ | ||
| + | from $ H ^ {2} $ | ||
| + | into $ L ^ {2} $ | ||
| + | satisfying $ UB = BT $, | ||
| + | $ \| B \| = \| A \| $ | ||
| + | and $ PB = A $. | ||
| + | Therefore, the error $ d _ \infty = \| A \| $, | ||
| + | and there exists an $ h \in H ^ \infty $ | ||
| + | such that $ d _ \infty = \| {f - h } \| _ \infty $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> C. Foias, A.E. Frazho, "The commutant lifting approach to interpolation problems" , ''Operator Theory: Advances and Applications'' , '''44''' , Birkhäuser (1990)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> C. Foias, H. Özbay, A. Tannenbaum, "Robust control of infinite-dimensional systems" , Springer (1996)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> D. Sarason, "Generalized interpolation in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c110/c110320/c11032080.png" />" ''Trans. Amer. Math. Soc.'' , '''127''' (1967) pp. 179–203</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> B. Sz.-Nagy, C. Foias, "Dilatation des commutants d'opérateurs" ''C.R. Acad. Sci. Paris'' , '''A266''' (1968) pp. 493–495</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> B. Sz.-Nagy, C. Foias, "Harmonic analysis of operators on Hilbert space" , North-Holland (1970)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> C. Foias, A.E. Frazho, "The commutant lifting approach to interpolation problems" , ''Operator Theory: Advances and Applications'' , '''44''' , Birkhäuser (1990)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> C. Foias, H. Özbay, A. Tannenbaum, "Robust control of infinite-dimensional systems" , Springer (1996)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> D. Sarason, "Generalized interpolation in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c110/c110320/c11032080.png" />" ''Trans. Amer. Math. Soc.'' , '''127''' (1967) pp. 179–203</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> B. Sz.-Nagy, C. Foias, "Dilatation des commutants d'opérateurs" ''C.R. Acad. Sci. Paris'' , '''A266''' (1968) pp. 493–495</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> B. Sz.-Nagy, C. Foias, "Harmonic analysis of operators on Hilbert space" , North-Holland (1970)</TD></TR></table> | ||
Revision as of 17:45, 4 June 2020
Let $ T _ {1} $
be a contraction on a Hilbert space $ {\mathcal H} _ {1} $,
that is, $ \| {T _ {1} } \| \leq 1 $.
Recall that $ U $
is an isometric dilation of $ T _ {1} $
if $ U $
is an isometry (cf. Isometric operator) on a Hilbert space $ {\mathcal K} \supseteq {\mathcal H} _ {1} $
and $ {\mathcal H} _ {1} $
is an invariant subspace for $ U ^ {*} $
satisfying $ U ^ {*} \mid {\mathcal H} _ {1} = T _ {1} ^ {*} $.
The Sz.-Nagy–Shäffer construction shows that all contractions admit an isometric dilation [a1], [a5]. This sets the stage for the following result, known as the Sz.-Nagy–Foias commutant lifting theorem [a1], [a4], [a5].
Let $ U $ on $ {\mathcal K} $ be an isometric dilation for a contraction $ T _ {1} $ on $ {\mathcal H} _ {1} $. Let $ A $ be an operator from the Hilbert space $ {\mathcal H} $ into $ {\mathcal H} _ {1} $ and $ T $ an isometry on $ {\mathcal H} $ satisfying $ T _ {1} A = AT $. Then there exists an operator $ B $ from $ {\mathcal H} $ into $ {\mathcal K} $ satisfying the following three conditions: $ UB = BT $, $ \| B \| = \| A \| $ and $ PB = A $, where $ P $ is the orthogonal projection onto $ {\mathcal H} _ {1} $.
The commutant lifting theorem was inspired by seminal work of D. Sarason [a3] on $ H ^ \infty $ interpolation. It can be used to solve many classical and modern $ H ^ \infty $ interpolation problems, including the Carathéodory, Nevanlinna–Pick, Hermite–Féjer, Nudelman, Nehari, and Löwner interpolation problems in both their classical and tangential form (see [a1] and also Carathéodory interpolation; Nevanlinna–Pick interpolation). The commutant lifting theorem can also be used to solve problems in $ H ^ \infty $ control theory and inverse scattering [a1], [a2].
There is a one-to-one correspondence between the set of all solutions in the commutant lifting theorem and a certain choice sequence of contractions. This choice sequence is a generalization of the Schur numbers used to solve the Carathéodory interpolation problem or the reflection coefficients appearing in inverse scattering problems for layered media in geophysics. There is also a one-to-one correspondence between the sets of all solutions for the commutant lifting theorem and a certain contractive analytic function in the open unit disc. This characterization of all solutions has several different network interpretations [a1].
As an illustration of the commutant lifting theorem, consider the Nehari interpolation problem
$$ d _ \infty = \inf \left \{ {\left \| {f - h } \right \| _ \infty } : {h \in H ^ \infty } \right \} , $$
where $ f $ is a given function in $ L ^ \infty $. Here, $ L ^ \infty $ is the Banach space of all Lebesgue-measurable functions $ g $ on the unit circle whose norm $ \| g \| _ \infty = { \mathop{\rm ess} \sup } \{ {| {g ( e ^ {it } ) } | } : {0 \leq t < 2 \pi } \} $ is finite, and $ H ^ \infty $ is the subspace of $ L ^ \infty $ consisting of all functions $ g $ in $ L ^ \infty $ whose Fourier coefficients at $ e ^ {int } $ are zero for all $ n < 0 $. Likewise, $ L ^ {2} $ is the Hilbert space of all Lebesgue-measurable, square-integrable functions on the unit circle, and $ H ^ {2} $ is the subspace of $ L ^ {2} $ consisting of all functions in $ L ^ {2} $ whose Fourier coefficients at $ e ^ {int } $ vanish for all $ n < 0 $. Now, let $ A $ be the Hankel operator from $ {\mathcal H} = H ^ {2} $ into $ {\mathcal H} _ {1} = L ^ {2} \omn H ^ {2} $ defined by $ Ax = Pfx $ for $ x $ in $ H ^ {2} $. Let $ T $ be the isometry on $ H ^ {2} $ and $ U $ the unitary operator on $ {\mathcal K} = L ^ {2} $ defined by $ Tx = e ^ {it } x $ and $ Uy = e ^ {it } y $, respectively. Let $ T _ {1} $ be the contraction on $ {\mathcal H} _ {1} $ defined by $ T _ {1} h _ {1} = PUh _ {1} $ for $ h _ {1} $ in $ {\mathcal H} _ {1} $. Since $ T _ {1} ^ {*} = U ^ {*} \mid {\mathcal H} _ {1} $, it follows that $ U $ is an isometric lifting of $ T _ {1} $. By applying the commutant lifting theorem, there exists an operator $ B $ from $ H ^ {2} $ into $ L ^ {2} $ satisfying $ UB = BT $, $ \| B \| = \| A \| $ and $ PB = A $. Therefore, the error $ d _ \infty = \| A \| $, and there exists an $ h \in H ^ \infty $ such that $ d _ \infty = \| {f - h } \| _ \infty $.
References
| [a1] | C. Foias, A.E. Frazho, "The commutant lifting approach to interpolation problems" , Operator Theory: Advances and Applications , 44 , Birkhäuser (1990) |
| [a2] | C. Foias, H. Özbay, A. Tannenbaum, "Robust control of infinite-dimensional systems" , Springer (1996) |
| [a3] | D. Sarason, "Generalized interpolation in 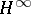 " Trans. Amer. Math. Soc. , 127 (1967) pp. 179–203 " Trans. Amer. Math. Soc. , 127 (1967) pp. 179–203 |
| [a4] | B. Sz.-Nagy, C. Foias, "Dilatation des commutants d'opérateurs" C.R. Acad. Sci. Paris , A266 (1968) pp. 493–495 |
| [a5] | B. Sz.-Nagy, C. Foias, "Harmonic analysis of operators on Hilbert space" , North-Holland (1970) |
Commutant lifting theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Commutant_lifting_theorem&oldid=46403