Difference between revisions of "Character of a C*-algebra"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | c0215402.png | ||
| + | $#A+1 = 35 n = 1 | ||
| + | $#C+1 = 35 : ~/encyclopedia/old_files/data/C021/C.0201540 Character of a \BMI C sup \ast\EMI\AAhalgebra | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | A non-zero lower semi-continuous semi-finite trace $ f $ | ||
| + | on a [[C*-algebra| $ C ^ {*} $- | ||
| + | algebra]] $ A $ | ||
| + | satisfying the following condition (cf. [[Trace on a C*-algebra|Trace on a $ C ^ {*} $- | ||
| + | algebra]]): If $ \phi $ | ||
| + | is a lower semi-continuous semi-finite trace on $ A $ | ||
| + | and if $ \phi ( x) \leq f ( x) $ | ||
| + | for all $ x \in A ^ {+} $, | ||
| + | then $ \phi ( x) = \lambda f ( x) $ | ||
| + | for a certain non-negative number $ \lambda $ | ||
| + | and all elements $ x \in A ^ {+} $ | ||
| + | in the closure of the ideal $ \mathfrak N _ {f} $ | ||
| + | generated by the set $ \{ {x } : {x \in A ^ {+} , f ( x) < + \infty } \} $. | ||
| + | There exists a canonical one-to-one correspondence between the set of quasi-equivalence classes of non-zero factor representations of $ A $ | ||
| + | admitting a trace and the set of characters of $ A $ | ||
| + | defined up to a positive multiplier (cf. [[Factor representation|Factor representation]]); this correspondence is established by the formula $ f ( x) = \chi ( \pi ( x)) $, | ||
| + | $ x \in A $, | ||
| + | where $ \pi $ | ||
| + | is the factor representation of $ A $ | ||
| + | admitting the trace $ \chi $. | ||
| + | If the trace $ f $ | ||
| + | on $ A $ | ||
| + | is finite, then the character is said to be finite; a finite character is continuous. There exists a canonical one-to-one correspondence between the set of quasi-equivalence classes of non-zero factor representations of finite type of a $ C ^ {*} $- | ||
| + | algebra $ A $ | ||
| + | and the set of finite characters of $ A $ | ||
| + | with norm 1. If $ A $ | ||
| + | is commutative, then any character of the commutative algebra $ A $ | ||
| + | is a character of the $ C ^ {*} $- | ||
| + | algebra $ A $. | ||
| + | If $ A $ | ||
| + | is the group $ C ^ {*} $- | ||
| + | algebra of a compact group $ G $, | ||
| + | then the characters of the $ C ^ {*} $- | ||
| + | algebra $ A $ | ||
| + | are finite, and to such a character with norm 1 there corresponds a normalized character of $ G $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> J. Dixmier, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021540/c02154038.png" /> algebras" , North-Holland (1977) (Translated from French)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J. Dixmier, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021540/c02154038.png" /> algebras" , North-Holland (1977) (Translated from French)</TD></TR></table> | ||
Revision as of 16:43, 4 June 2020
A non-zero lower semi-continuous semi-finite trace $ f $
on a $ C ^ {*} $-
algebra $ A $
satisfying the following condition (cf. Trace on a $ C ^ {*} $-
algebra): If $ \phi $
is a lower semi-continuous semi-finite trace on $ A $
and if $ \phi ( x) \leq f ( x) $
for all $ x \in A ^ {+} $,
then $ \phi ( x) = \lambda f ( x) $
for a certain non-negative number $ \lambda $
and all elements $ x \in A ^ {+} $
in the closure of the ideal $ \mathfrak N _ {f} $
generated by the set $ \{ {x } : {x \in A ^ {+} , f ( x) < + \infty } \} $.
There exists a canonical one-to-one correspondence between the set of quasi-equivalence classes of non-zero factor representations of $ A $
admitting a trace and the set of characters of $ A $
defined up to a positive multiplier (cf. Factor representation); this correspondence is established by the formula $ f ( x) = \chi ( \pi ( x)) $,
$ x \in A $,
where $ \pi $
is the factor representation of $ A $
admitting the trace $ \chi $.
If the trace $ f $
on $ A $
is finite, then the character is said to be finite; a finite character is continuous. There exists a canonical one-to-one correspondence between the set of quasi-equivalence classes of non-zero factor representations of finite type of a $ C ^ {*} $-
algebra $ A $
and the set of finite characters of $ A $
with norm 1. If $ A $
is commutative, then any character of the commutative algebra $ A $
is a character of the $ C ^ {*} $-
algebra $ A $.
If $ A $
is the group $ C ^ {*} $-
algebra of a compact group $ G $,
then the characters of the $ C ^ {*} $-
algebra $ A $
are finite, and to such a character with norm 1 there corresponds a normalized character of $ G $.
References
| [1] | J. Dixmier, "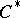 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
Character of a C*-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Character_of_a_C*-algebra&oldid=46312