Difference between revisions of "Calderón-Zygmund operator"
Ulf Rehmann (talk | contribs) m (moved Calderon-Zygmund operator to Calderón-Zygmund operator: accented title) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | c0200701.png | ||
| + | $#A+1 = 37 n = 1 | ||
| + | $#C+1 = 37 : ~/encyclopedia/old_files/data/C020/C.0200070 Calder\Aeon\ANDZygmund operator | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | An operator $ K $ | |
| + | defined on a space of sufficiently smooth functions $ \phi $ | ||
| + | with compact support in $ \mathbf R ^ {n} $ | ||
| + | by the formula | ||
| − | + | $$ | |
| + | K \phi (x) = \ | ||
| + | \lim\limits _ {\epsilon \rightarrow 0 } \ | ||
| + | \int\limits _ {| x - y | > \epsilon } | ||
| + | k (x - y) \phi (y) dy, | ||
| + | $$ | ||
| − | where | + | where the kernel $ k $ |
| + | is a homogeneous function of degree $ -n $ | ||
| + | with zero mean value over the unit sphere $ S ^ {n - 1 } = \{ {x } : {x \in \mathbf R ^ {n} , | x | = 1 } \} $. | ||
| + | The kernel $ k $ | ||
| + | has the form | ||
| − | + | $$ | |
| + | k (x) = \ | ||
| − | + | \frac{\Omega (x) }{| x | ^ {n} } | |
| + | , | ||
| + | $$ | ||
| + | |||
| + | where $ \Omega $, | ||
| + | the characteristic function of $ k $, | ||
| + | satisfies the conditions | ||
| + | |||
| + | $$ \tag{* } | ||
| + | \Omega (tx) = \ | ||
| + | \Omega (x) \ \ | ||
| + | \textrm{ for } \ | ||
| + | t > 0,\ | ||
| + | \Omega \in L _ {1} (S), | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | \int\limits _ { S } \Omega (x) dS = 0. | ||
| + | $$ | ||
The Calderón–Zygmund operator is usually written in the form | The Calderón–Zygmund operator is usually written in the form | ||
| − | + | $$ | |
| + | K \phi (x) = \ | ||
| + | \textrm{ p.v. } | ||
| + | \int\limits _ {\mathbf R ^ {n} } | ||
| + | \phi (y) | ||
| − | + | \frac{\Omega (x - y) }{| x - y | ^ {n} } | |
| + | \ | ||
| + | dy; | ||
| + | $$ | ||
| − | + | here $ \textrm{ p }.v. $ | |
| + | denotes the principal value of the integral. In the one-dimensional case the Calderón–Zygmund operator becomes the Hilbert operator $ H $: | ||
| − | + | $$ | |
| + | H \phi (x) = \ | ||
| + | \textrm{ p.v. } | ||
| + | \int\limits _ {- \infty } ^ \infty | ||
| − | < | + | \frac{\phi (t) }{x - t } |
| + | dt. | ||
| + | $$ | ||
| + | |||
| + | The Calderón–Zygmund operator can be extended by continuity to the space $ L _ {p} ( \mathbf R ^ {n} ) $ | ||
| + | of functions $ f $ | ||
| + | in $ \mathbf R ^ {n} $ | ||
| + | that are summable of degree $ p $ | ||
| + | $ (1 < p < \infty ) $. | ||
| + | This extension maps $ L _ {p} ( \mathbf R ^ {n} ) $ | ||
| + | continuously into itself. If $ \Omega $ | ||
| + | satisfies the condition (*) and also Dini's condition: | ||
| + | |||
| + | $$ | ||
| + | \int\limits _ { 0 } ^ { 1 } | ||
| + | { | ||
| + | \frac{\omega (t) dt }{t} | ||
| + | } < \infty ,\ \ | ||
| + | \omega (t) = \ | ||
| + | \sup _ | ||
| + | {\begin{array}{c} | ||
| + | | x - x ^ \prime | \leq t \\ | ||
| + | | x | = | x ^ \prime | = 1 | ||
| + | \end{array} | ||
| + | } \ | ||
| + | | \Omega (x) - \Omega (x ^ \prime ) | ; | ||
| + | $$ | ||
and if | and if | ||
| − | + | $$ | |
| + | K _ \epsilon f (x) = \ | ||
| + | \int\limits _ {| y | > \epsilon } | ||
| − | + | \frac{\Omega (y) }{| y | ^ {n} } | |
| − | + | f (x - y) dy | |
| + | $$ | ||
| − | < | + | for $ 1 < p < \infty $ |
| + | and $ f \in L _ {p} ( \mathbf R ^ {n} ) $, | ||
| + | then | ||
| − | + | a) there exists a constant $ A _ {p} $( | |
| + | independent of $ f $ | ||
| + | or $ \epsilon $) | ||
| + | such that | ||
| − | + | $$ | |
| + | \| K _ \epsilon f \| _ {L _ {p} } \leq \ | ||
| + | A _ {p} \| f \| _ {L _ {p} } ; | ||
| + | $$ | ||
| + | |||
| + | b) the limit $ \lim\limits _ {\epsilon \rightarrow 0 } K _ \epsilon f = Kf $ | ||
| + | exists in the sense of convergence in $ L _ {p} $ | ||
| + | and | ||
| + | |||
| + | $$ | ||
| + | \| Kf \| _ {L _ {p} } \leq \ | ||
| + | A _ {p} \| f \| _ {L _ {p} } . | ||
| + | $$ | ||
The Calderón–Zygmund operator was analyzed by A.P. Calderón and A. Zygmund [[#References|[1]]]. | The Calderón–Zygmund operator was analyzed by A.P. Calderón and A. Zygmund [[#References|[1]]]. | ||
| Line 43: | Line 139: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.P. Calderón, A. Zygmund, "On the existence of certain singular integrals" ''Acta Math.'' , '''88''' (1952) pp. 85–139</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.G. Mikhlin, "Multidimensional singular integrals and integral equations" , Pergamon (1965) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.M. Stein, "Singular integrals and differentiability properties of functions" , Princeton Univ. Press (1970)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.P. Calderón, A. Zygmund, "On the existence of certain singular integrals" ''Acta Math.'' , '''88''' (1952) pp. 85–139</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.G. Mikhlin, "Multidimensional singular integrals and integral equations" , Pergamon (1965) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.M. Stein, "Singular integrals and differentiability properties of functions" , Princeton Univ. Press (1970)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Proofs of the estimates a) and b) above can be found in [[#References|[3]]], Chapt. II, Section 4. | Proofs of the estimates a) and b) above can be found in [[#References|[3]]], Chapt. II, Section 4. | ||
| − | In the 1960's the operators described above were often called Mikhlin–Calderón–Zygmund operators, since the main boundedness theorem for them on | + | In the 1960's the operators described above were often called Mikhlin–Calderón–Zygmund operators, since the main boundedness theorem for them on $ L _ {p} ( \mathbf R ^ {n} ) $( |
| + | estimate a)) was proved by S.G. Mikhlin in 1938 (published in [[#References|[a1]]]). | ||
Nowadays the term Calderón–Zygmund operator is often used for general operators in the class defined by G. David and J.L. Journé in [[#References|[a2]]]. | Nowadays the term Calderón–Zygmund operator is often used for general operators in the class defined by G. David and J.L. Journé in [[#References|[a2]]]. | ||
| − | Assertion b) has been generalized to singular integrals with odd kernels, and to singular integrals with even kernels | + | Assertion b) has been generalized to singular integrals with odd kernels, and to singular integrals with even kernels $ \Omega \in L _ {2} (S ^ {n - 1 } ) $, |
| + | [[#References|[a3]]], Chapt. VI, Sections 2, 3. | ||
See also [[Singular integral|Singular integral]]; [[Hilbert singular integral|Hilbert singular integral]]; [[Hilbert transform|Hilbert transform]]. | See also [[Singular integral|Singular integral]]; [[Hilbert singular integral|Hilbert singular integral]]; [[Hilbert transform|Hilbert transform]]. | ||
Revision as of 06:29, 30 May 2020
An operator $ K $
defined on a space of sufficiently smooth functions $ \phi $
with compact support in $ \mathbf R ^ {n} $
by the formula
$$ K \phi (x) = \ \lim\limits _ {\epsilon \rightarrow 0 } \ \int\limits _ {| x - y | > \epsilon } k (x - y) \phi (y) dy, $$
where the kernel $ k $ is a homogeneous function of degree $ -n $ with zero mean value over the unit sphere $ S ^ {n - 1 } = \{ {x } : {x \in \mathbf R ^ {n} , | x | = 1 } \} $. The kernel $ k $ has the form
$$ k (x) = \ \frac{\Omega (x) }{| x | ^ {n} } , $$
where $ \Omega $, the characteristic function of $ k $, satisfies the conditions
$$ \tag{* } \Omega (tx) = \ \Omega (x) \ \ \textrm{ for } \ t > 0,\ \Omega \in L _ {1} (S), $$
$$ \int\limits _ { S } \Omega (x) dS = 0. $$
The Calderón–Zygmund operator is usually written in the form
$$ K \phi (x) = \ \textrm{ p.v. } \int\limits _ {\mathbf R ^ {n} } \phi (y) \frac{\Omega (x - y) }{| x - y | ^ {n} } \ dy; $$
here $ \textrm{ p }.v. $ denotes the principal value of the integral. In the one-dimensional case the Calderón–Zygmund operator becomes the Hilbert operator $ H $:
$$ H \phi (x) = \ \textrm{ p.v. } \int\limits _ {- \infty } ^ \infty \frac{\phi (t) }{x - t } dt. $$
The Calderón–Zygmund operator can be extended by continuity to the space $ L _ {p} ( \mathbf R ^ {n} ) $ of functions $ f $ in $ \mathbf R ^ {n} $ that are summable of degree $ p $ $ (1 < p < \infty ) $. This extension maps $ L _ {p} ( \mathbf R ^ {n} ) $ continuously into itself. If $ \Omega $ satisfies the condition (*) and also Dini's condition:
$$ \int\limits _ { 0 } ^ { 1 } { \frac{\omega (t) dt }{t} } < \infty ,\ \ \omega (t) = \ \sup _ {\begin{array}{c} | x - x ^ \prime | \leq t \\ | x | = | x ^ \prime | = 1 \end{array} } \ | \Omega (x) - \Omega (x ^ \prime ) | ; $$
and if
$$ K _ \epsilon f (x) = \ \int\limits _ {| y | > \epsilon } \frac{\Omega (y) }{| y | ^ {n} } f (x - y) dy $$
for $ 1 < p < \infty $ and $ f \in L _ {p} ( \mathbf R ^ {n} ) $, then
a) there exists a constant $ A _ {p} $( independent of $ f $ or $ \epsilon $) such that
$$ \| K _ \epsilon f \| _ {L _ {p} } \leq \ A _ {p} \| f \| _ {L _ {p} } ; $$
b) the limit $ \lim\limits _ {\epsilon \rightarrow 0 } K _ \epsilon f = Kf $ exists in the sense of convergence in $ L _ {p} $ and
$$ \| Kf \| _ {L _ {p} } \leq \ A _ {p} \| f \| _ {L _ {p} } . $$
The Calderón–Zygmund operator was analyzed by A.P. Calderón and A. Zygmund [1].
References
| [1] | A.P. Calderón, A. Zygmund, "On the existence of certain singular integrals" Acta Math. , 88 (1952) pp. 85–139 |
| [2] | S.G. Mikhlin, "Multidimensional singular integrals and integral equations" , Pergamon (1965) (Translated from Russian) |
| [3] | E.M. Stein, "Singular integrals and differentiability properties of functions" , Princeton Univ. Press (1970) |
Comments
Proofs of the estimates a) and b) above can be found in [3], Chapt. II, Section 4.
In the 1960's the operators described above were often called Mikhlin–Calderón–Zygmund operators, since the main boundedness theorem for them on $ L _ {p} ( \mathbf R ^ {n} ) $( estimate a)) was proved by S.G. Mikhlin in 1938 (published in [a1]).
Nowadays the term Calderón–Zygmund operator is often used for general operators in the class defined by G. David and J.L. Journé in [a2].
Assertion b) has been generalized to singular integrals with odd kernels, and to singular integrals with even kernels $ \Omega \in L _ {2} (S ^ {n - 1 } ) $, [a3], Chapt. VI, Sections 2, 3.
See also Singular integral; Hilbert singular integral; Hilbert transform.
References
| [a1] | S.G. Mikhlin, "On a boundedness theorem for a singular integral operator" Uspekhi Mat. Nauk , 8 (1953) pp. 213–217 (In Russian) |
| [a2] | G. David, J.L. Journé, "Une characterization des opérateurs intégraux singuliers bornés sur 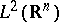 " C.R. Acad. Sci. Paris , 296 (1983) pp. 761–764 " C.R. Acad. Sci. Paris , 296 (1983) pp. 761–764 |
| [a3] | E.M. Stein, G. Weiss, "Fourier analysis on Euclidean spaces" , Princeton Univ. Press (1975) |
Calderón-Zygmund operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Calder%C3%B3n-Zygmund_operator&oldid=46187