Difference between revisions of "Braid theory"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | b0174702.png | ||
| + | $#A+1 = 281 n = 0 | ||
| + | $#C+1 = 281 : ~/encyclopedia/old_files/data/B017/B.0107470 Braid theory | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
The branch of topology and algebra concerned with braids, the groups formed by their equivalence classes and various generalizations of these groups [[#References|[1]]]. | The branch of topology and algebra concerned with braids, the groups formed by their equivalence classes and various generalizations of these groups [[#References|[1]]]. | ||
| − | A braid on | + | A braid on $ n $ |
| + | strings is an object consisting of two parallel planes $ P _ {0} $ | ||
| + | and $ P _ {1} $ | ||
| + | in three-dimensional space $ \mathbf R ^ {3} $, | ||
| + | containing two ordered sets of points $ a _ {1} \dots a _ {n} \in P _ {0} $ | ||
| + | and $ b _ {1} \dots b _ {n} \in P _ {1} $, | ||
| + | and of $ n $ | ||
| + | simple non-intersecting arcs $ l _ {1} \dots l _ {n} $, | ||
| + | intersecting each parallel plane $ P _ {t} $ | ||
| + | between $ P _ {0} $ | ||
| + | and $ P _ {1} $ | ||
| + | exactly once and joining the points $ \{ a _ {i} \} $ | ||
| + | to $ \{ b _ {i} \} $, | ||
| + | $ i = 1 \dots n $. | ||
| + | It is assumed that the $ a _ {i} $' | ||
| + | s lie on a straight line $ L _ {a} $ | ||
| + | in $ P _ {0} $ | ||
| + | and the $ b _ {i} $' | ||
| + | s on a straight line $ L _ {b} $ | ||
| + | in $ P _ {1} $ | ||
| + | parallel to $ L _ {a} $; | ||
| + | moreover, $ b _ {i} $ | ||
| + | lies beneath $ a _ {i} $ | ||
| + | for each $ i $( | ||
| + | see Fig. a). Braids can be represented in the projection on the plane passing through $ L _ {a} $ | ||
| + | and $ L _ {b} $; | ||
| + | this projection can be brought into general position in such a way that there are only finitely many double points, each two of which lie at different levels, and the intersections are transversal. | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/b017470a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/b017470a.gif" /> | ||
| Line 11: | Line 49: | ||
Figure: b017470b | Figure: b017470b | ||
| − | The string | + | The string $ l _ {i} $ |
| + | of a braid $ \omega $ | ||
| + | joins $ a _ {i} $ | ||
| + | to $ b _ {k _ {i} } $ | ||
| + | and so defines a permutation | ||
| − | + | $$ | |
| + | S ^ \omega = \ | ||
| + | \left ( \ | ||
| − | + | \begin{array}{ccc} | |
| + | 1 &\dots & n \\ | ||
| + | k _ {1} &\dots &k _ {n} \\ | ||
| + | \end{array} | ||
| + | \ | ||
| + | \right ) . | ||
| + | $$ | ||
| − | + | If this is the identity permutation, $ \omega $ | |
| + | is called a coloured (or pure) braid. The transposition $ (i i + 1) $ | ||
| + | corresponds to a simple braid $ \sigma _ {i} $( | ||
| + | see Fig. b). | ||
| − | The equivalence classes — which are still called braids — form the braid group | + | On the set of all braids on $ n $ |
| + | strings with fixed $ P _ {0} $, | ||
| + | $ P _ {1} $, | ||
| + | $ \{ a _ {i} \} $, | ||
| + | $ \{ b _ {i} \} $, | ||
| + | one introduces the equivalence relation defined by homeomorphisms $ h: \Pi \rightarrow \Pi $, | ||
| + | where $ \Pi $ | ||
| + | is the region between $ P _ {0} $ | ||
| + | and $ P _ {1} $, | ||
| + | which reduce to the identity on $ P _ {0} \cup P _ {1} $; | ||
| + | it may be assumed that $ h (P _ {t} ) = P _ {t} $. | ||
| + | Braids $ \alpha $ | ||
| + | and $ \beta $ | ||
| + | are equivalent if there exists a homeomorphism with the above properties such that $ h ( \alpha ) = \beta $. | ||
| + | |||
| + | The equivalence classes — which are still called braids — form the braid group $ B (n) $ | ||
| + | with respect to the operation defined as follows. Place a copy $ \Pi ^ \prime $ | ||
| + | of the domain $ \Pi $ | ||
| + | above another copy $ \Pi ^ {\prime\prime} $, | ||
| + | in such a way that $ P _ {0} ^ {\prime\prime} $ | ||
| + | coincides with $ P _ {1} ^ \prime $, | ||
| + | $ a _ {i} ^ {\prime\prime} $ | ||
| + | with $ b _ {i} ^ \prime $, | ||
| + | and then compress $ \Pi ^ \prime \cup \Pi ^ {\prime\prime} $ | ||
| + | to half its "height" . The images of the braids $ \omega ^ \prime \in \Pi ^ \prime $ | ||
| + | and $ \omega ^ {\prime\prime} \in \Pi ^ {\prime\prime} $ | ||
| + | produce a braid $ \omega ^ \prime \omega ^ {\prime\prime} $, | ||
| + | with string $ l _ {i} $ | ||
| + | obtained by extending $ l _ {i} ^ \prime $ | ||
| + | with $ l _ {k _ {i} } ^ {\prime\prime} $, | ||
| + | where $ k _ {i} \in S ^ {\omega ^ \prime (i) } $. | ||
| + | The identity braid is the equivalence class containing the braid with $ n $ | ||
| + | parallel segments; the inverse $ \omega ^ {-1} $ | ||
| + | of a braid $ \omega $ | ||
| + | is defined by reflection in the plane $ P _ {1/2} $. | ||
| + | For the condition $ \omega \omega ^ {-1} = \epsilon $ | ||
| + | see Fig. c. | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/b017470c.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/b017470c.gif" /> | ||
| Line 25: | Line 114: | ||
Figure: b017470c | Figure: b017470c | ||
| − | The mapping | + | The mapping $ \omega \rightarrow S ^ \omega $ |
| + | defines an epimorphism of $ B (n) $ | ||
| + | onto the group $ S (n) $ | ||
| + | of permutations of $ n $ | ||
| + | elements, the kernel of this epimorphism is the subgroup $ K (n) $ | ||
| + | of all pure braids, so that one has an exact sequence | ||
| − | + | $$ | |
| + | 1 \rightarrow K (n) \rightarrow B (n) \rightarrow S (n) \rightarrow 1. | ||
| + | $$ | ||
| − | The braid group | + | The braid group $ B (n) $ |
| + | has two principal interpretations. The first, as a configuration space, is obtained by identifying the planes $ P _ {t} $ | ||
| + | via vertical projection onto $ P _ {0} $, | ||
| + | under which the images of the points $ a _ {it } = l _ {i} \cap P _ {t} $, | ||
| + | considered as $ t $ | ||
| + | varies from 0 to 1, form the trace of an isotopy $ \phi _ {t} ^ \omega $ | ||
| + | of the set $ \cup a _ {i} $ | ||
| + | along $ P _ {0} $; | ||
| + | one has $ \phi _ {1} ^ \omega ( \cup a _ {i} ) = \cup a _ {i} $. | ||
| + | Consider the space of unordered sequences $ G (n) $ | ||
| + | of $ n $ | ||
| + | pairwise distinct points of the plane; then each braid corresponds in one-to-one fashion to a class of homotopy loops in this space, and one has an isomorphism | ||
| − | + | $$ | |
| + | \beta : B (n) \rightarrow \ | ||
| + | \pi _ {1} G (n). | ||
| + | $$ | ||
For pure braids one has an analogously constructed isomorphism | For pure braids one has an analogously constructed isomorphism | ||
| − | + | $$ | |
| + | \alpha : K (n) \rightarrow \ | ||
| + | \pi _ {1} F (n), | ||
| + | $$ | ||
| − | where | + | where $ F (n) $ |
| + | is the space of ordered sequences of $ n $ | ||
| + | distinct points of the plane, so that $ K (n) $ | ||
| + | can be identified with the subgroup corresponding to the covering | ||
| − | + | $$ | |
| + | p: F (n) \rightarrow G (n) = \ | ||
| + | F (n) / S (n). | ||
| + | $$ | ||
| − | The second interpretation, as a homeotopy group, is obtained by extending the isotopy | + | The second interpretation, as a homeotopy group, is obtained by extending the isotopy $ \phi _ {t} ^ \omega $ |
| + | to an isotopy $ {\widetilde \phi } {} _ {t} ^ \omega $ | ||
| + | of the plane $ P _ {0} $ | ||
| + | that coincides with the identity outside some disc, and such that $ {\widetilde \phi } {} _ {0} ^ \omega = \mathop{\rm id} $. | ||
| + | For each $ t $, | ||
| + | two such extensions differ by a homeomorphism which is the identity at the points $ a _ {it} $. | ||
| + | A braid uniquely determines a component of the space of homeomorphisms $ Y (n) $ | ||
| + | of the plane which map the set $ \cup a _ {i} $ | ||
| + | onto itself, and one has an isomorphism | ||
| − | + | $$ | |
| + | \gamma : B (n) \rightarrow \ | ||
| + | \pi _ {0} Y (n). | ||
| + | $$ | ||
| − | To each homeomorphism | + | To each homeomorphism $ h \in Y $ |
| + | corresponds an automorphism of the free group of rank $ n: $ | ||
| + | $ F _ {n} = \pi _ {1} ( \mathbf R ^ {2} \setminus \cup a _ {i} ) $, | ||
| + | defined up to an inner automorphism, which in turn yields a homomorphism $ B (n) \rightarrow \mathop{\rm Out} F _ {n} = \mathop{\rm Aut} F _ {n} / \mathop{\rm Inn} F _ {n} $. | ||
| + | The elements of the image are called braid automorphisms of the free group. In particular, corresponding to the braid $ \sigma _ {i} $ | ||
| + | one has an automorphism | ||
| − | + | $$ | |
| + | \overline \sigma \; _ {i} :\ | ||
| + | \overline \sigma \; _ {i} (x _ {i} ) = \ | ||
| + | x _ {i + 1 } ,\ \ | ||
| + | \overline \sigma \; _ {i} (x _ {i + 1 } ) = \ | ||
| + | x _ {i + 1 } x _ {i} x _ {i + 1 } ^ {-1} ,\ \ | ||
| + | \overline \sigma \; _ {i} (x _ {j} ) = x _ {j} , | ||
| + | $$ | ||
| − | if | + | if $ j \neq i, i + 1 $( |
| + | $ \{ x _ {i} \} $ | ||
| + | is a set of generators of $ F _ {n} $). | ||
| + | Any braid automorphism $ \alpha $ | ||
| + | possesses the following properties: | ||
| − | + | $$ | |
| + | \alpha (x _ {i} ) = \ | ||
| + | A _ {i} x _ {i} A _ {i} ^ {-1} ,\ \ | ||
| + | \alpha \left ( \prod _ {i = 1 } ^ { n } x _ {i} \right ) = \ | ||
| + | \prod _ {i = 1 } ^ { n } x _ {i} , | ||
| + | $$ | ||
| − | up to an inner automorphism (for the meaning of | + | up to an inner automorphism (for the meaning of $ A _ {i} $, |
| + | see below); these properties characterize braid automorphisms. | ||
| − | The braids | + | The braids $ \sigma _ {i} , 1 \leq i \leq n - 1 $, |
| + | are the generators of the group $ B (n) $, | ||
| + | i.e. $ \omega = \sigma _ {k _ {1} } \dots \sigma _ {k _ {m} } $, | ||
| + | with | ||
| − | + | $$ \tag{1 } | |
| + | \left . | ||
| − | It turns out that (1) is a presentation of | + | \begin{array}{ll} |
| + | \sigma _ {i} \sigma _ {j} = \ | ||
| + | \sigma _ {j} \sigma _ {i} & \textrm{ if } | i - j | > 1, \\ | ||
| + | \sigma _ {i} \sigma _ {i + 1 } \sigma _ {i} = \ | ||
| + | \sigma _ {i + 1 } \sigma _ {i} \sigma _ {i - 1 } , & 1 \leq i \leq n - 2. \\ | ||
| + | \end{array} | ||
| + | \ | ||
| + | \right \} | ||
| + | $$ | ||
| + | |||
| + | It turns out that (1) is a presentation of $ B (n) $( | ||
| + | see Fig. d). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/b017470d.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/b017470d.gif" /> | ||
| Line 69: | Line 236: | ||
Figure: b017470e | Figure: b017470e | ||
| − | There exists a splitting exact sequence (obtained from the locally trivial fibration | + | There exists a splitting exact sequence (obtained from the locally trivial fibration $ F (n) \rightarrow F (n - 1) $ |
| + | with fibre $ \mathbf R ^ {2} \setminus (a _ {1} \dots a _ {n - 1 } ) $): | ||
| − | + | $$ | |
| + | 1 \rightarrow F _ {n - 1 } \rightarrow K (n) \rightarrow \ | ||
| + | K (n - 1) \rightarrow 1, | ||
| + | $$ | ||
which leads to the normal series | which leads to the normal series | ||
| − | + | $$ | |
| + | K (n) = \ | ||
| + | A _ {n} \supset \dots \supset \ | ||
| + | A _ {1} \supset A _ {0} = \ | ||
| + | F _ {n - 1 } | ||
| + | $$ | ||
| − | with free factors | + | with free factors $ A _ {i} / A _ {i - 1 } $, |
| + | where $ A _ {i} $ | ||
| + | has a "component" $ U _ {n - i } $ | ||
| + | isomorphic to $ K (n - i - 1) $. | ||
| + | Each element $ \omega \in B (n) $ | ||
| + | can be expressed uniquely in the form | ||
| − | + | $$ | |
| + | \omega = \ | ||
| + | \omega _ {2} \dots \omega _ {n} \pi _ \omega , | ||
| + | $$ | ||
| − | where | + | where $ \pi _ \omega $ |
| + | is a selected representative for $ S ^ \omega $ | ||
| + | in $ B (n) $ | ||
| + | and $ \omega _ {i} \in A _ {n - i + 1 } \cap U _ {i} $. | ||
| + | The reduction of a braid to this form is known as its dressing. This solves the word (identity) problem in $ B (n) $. | ||
| − | A presentation of | + | A presentation of $ K (n) $ |
| + | is as follows: generators (see Fig. e): | ||
| − | + | $$ | |
| + | A _ {ij} = \ | ||
| + | \sigma _ {j - 1 } \sigma _ {j} \sigma _ {j + 1 } \sigma _ {i} ^ {2} | ||
| + | \sigma _ {j + 1 } \sigma _ {j} \sigma _ {j - 1 } \in A _ {i} \cap U _ {n - i + 1 } ; | ||
| + | $$ | ||
relations: | relations: | ||
| − | < | + | $$ \tag{2 } |
| + | \left . | ||
| + | |||
| + | \begin{array}{ll} | ||
| + | A _ {rs} A _ {ij} = A _ {ij} A _ {rs} &\textrm{ if } r \leq s < i < j \\ | ||
| + | {} &\textrm{ or } i < r < s < j; \\ | ||
| + | A _ {rj} A _ {ij} = A _ {rj} &\textrm{ if } i = s; \\ | ||
| + | A _ {ij} A _ {sj} A _ {ij} A _ {ij} = A _ {sj} &\textrm{ if } r = i < j < s; \\ | ||
| + | A _ {rj} A _ {sj} A _ {rj} ^ {-1} | ||
| + | A _ {sj} ^ {-1} A _ {ij} A _ {rj} A _ {sj} = \ | ||
| + | A _ {sj} A _ {rj} &\textrm{ if } r < i < s < j. \\ | ||
| + | \end{array} | ||
| + | |||
| + | \right \} | ||
| + | $$ | ||
| − | This presentation may be obtained as a presentation of the kernel of the natural homomorphism into | + | This presentation may be obtained as a presentation of the kernel of the natural homomorphism into $ S (n) $ |
| + | of the abstract group $ B (n) $ | ||
| + | defined by the presentation (1) with the aid of the [[Schreier system|Schreier system]] $ \prod _ {j = 2 } ^ {n} M _ {j} k _ {j} $, | ||
| + | $ j \geq k _ {j} \geq n $, | ||
| + | where $ M _ {ji} = \sigma _ {j - 1 } \dots \sigma _ {i} $. | ||
| − | The centre of | + | The centre of $ B (n) $ |
| + | is the infinite cyclic group generated by the element $ ( \sigma _ {1} \dots \sigma _ {n} ) ^ {n} $. | ||
| + | The commutator group $ B ^ { \prime } (n) $ | ||
| + | coincides with $ B ^ { \prime\prime } (n) $ | ||
| + | for $ n \geq 5 $; | ||
| + | $ B ^ { \prime } (3) $ | ||
| + | is isomorphic to the free group of rank 2, and $ B ^ { \prime } (4) $ | ||
| + | is isomorphic to semi-direct product of two such groups. The quotient group modulo the commutator subgroup is an infinite cyclic group, generated by the images of $ \sigma _ {i} $. | ||
| + | There are no elements of finite order in $ B (n) $. | ||
| + | The group $ K (n) $ | ||
| + | is mapped onto itself by endomorphisms with non-Abelian image. In particular, $ K (n) \cap B ^ { \prime } (n) $ | ||
| + | is a fully-characteristic subgroup of $ B (n) $, | ||
| + | and also of $ K (n) $( | ||
| + | see [[#References|[15]]]). | ||
| − | Solving the conjugacy problem in | + | Solving the conjugacy problem in $ B (n) $ |
| + | is much more complicated than solving the word problem. There is a unique Garside normal form of a braid, $ \omega = \Delta ^ {m} \Omega $, | ||
| + | where $ \Delta = ( \sigma _ {1} {} \dots \sigma _ {n - 1 } ) ( \sigma _ {1} \dots \sigma _ {n - 2 } ) \dots ( \sigma _ {1} \sigma _ {2} ) \sigma _ {1} $ | ||
| + | is what is known as a Garside element and $ \Omega $ | ||
| + | is a positive braid, i.e. a braid the representation of which in terms of the elements $ \sigma _ {i} $ | ||
| + | has positive indices. With any braid $ \omega $ | ||
| + | one can associate, using finitely many operations depending on $ i $( | ||
| + | conjugation with certain elements, choice of elements of maximum degree, etc.), a certain set of words $ \Sigma ( \omega ) $, | ||
| + | from which one selects a word in normal form $ \Delta ^ {+} T $ | ||
| + | with minimal $ T $. | ||
| + | This is a so-called upper form of the braid $ \omega $. | ||
| + | It turns out that two braids are conjugate if and only if they have a same upper form (see [[#References|[7]]]). | ||
| − | The Burau representation of the braid group | + | The Burau representation of the braid group $ B (n) $ |
| + | in the group of matrices over the ring of polynomials in one variable with integer coefficients is defined by the correspondence | ||
| − | + | $$ | |
| + | b ( \omega ): \sigma _ {i} \rightarrow \ | ||
| + | \left \| | ||
| − | + | \begin{array}{cccc} | |
| + | I _ {i - 1 } & 0 & 0 & 0 \\ | ||
| + | 0 &i - t & t & 0 \\ | ||
| + | 0 & 1 & 0 & 0 \\ | ||
| + | 0 & 0 & 0 &I _ {n - k - 1 } \\ | ||
| + | \end{array} | ||
| + | \ | ||
| + | \right \| , | ||
| + | $$ | ||
| − | + | where $ I _ {k} $ | |
| + | is the identity matrix of order $ k $. | ||
| + | The matrix $ b ( \omega ) - I _ {n} $ | ||
| + | is the reduced Alexander matrix (see [[Alexander invariants|Alexander invariants]]) of the link obtained by closing the braid $ \omega $( | ||
| + | see below). For a pure braid one obtains the full Alexander matrix from the analogous Gassner matrix. The problem of whether these representations are faithful is still (1982) unsolved (see [[#References|[2]]]). | ||
| − | The | + | The fact that the spaces $ F (n) $ |
| + | and $ G (n) $ | ||
| + | are aspherical makes it possible to evaluate the homology of braid groups. | ||
| − | + | The homology of $ K (n) $( | |
| + | see [[#References|[16]]]). Homologically, $ K (n) $ | ||
| + | coincides with the product of unions of circles in which the number of circles runs from one through $ n - 1 $. | ||
| + | The homology ring is isomorphic to the exterior graded ring generated by the one-dimensional elements $ \omega _ {ij} = \omega _ {ji} $, | ||
| + | $ 1 \leq i \leq j \leq n $, | ||
| + | with relations | ||
| − | + | $$ | |
| + | \omega _ {kl} \omega _ {lm} + | ||
| + | \omega _ {lm} \omega _ {mk} + | ||
| + | \omega _ {mk} \omega _ {kl} = 0. | ||
| + | $$ | ||
| − | + | As $ \omega _ {kl} $ | |
| + | one can take the forms | ||
| − | + | $$ | |
| − | + | \frac{1}{2 \pi i } | |
| − | There is a natural mapping of | + | \frac{dz _ {k} - dz _ {l} }{z _ {k} - z _ {l} } |
| + | , | ||
| + | $$ | ||
| + | |||
| + | corresponding to passage along the diagonals $ z _ {k} = z _ {l} $. | ||
| + | |||
| + | The homology of $ B (n) $( | ||
| + | see [[#References|[8]]], [[#References|[12]]]). The homomorphism $ B (n) \rightarrow S (n) $ | ||
| + | can be extended to an imbedding $ S (n) \rightarrow O (n) $; | ||
| + | the induced homomorphism of cohomology spaces $ H ^ {*} (O (n)) \rightarrow H ^ {*} (B (n)) $ | ||
| + | is epimorphic, i.e. the cohomology spaces $ \mathop{\rm mod} 2 $ | ||
| + | of the group $ B (n) $ | ||
| + | generated by the Stiefel–Whitney classes. | ||
| + | |||
| + | There is a natural mapping of $ G (n) $ | ||
| + | into $ \Omega ^ {2} S ^ {2} $, | ||
| + | the two-fold loop space of $ S ^ {2} $, | ||
| + | i.e. the space of spheroids $ S ^ {2} \rightarrow S ^ {2} $( | ||
| + | choose small discs about $ n $ | ||
| + | points, then map these discs canonically with degree 1 into a sphere, mapping the entire complement onto a point). This mapping (see [[#References|[14]]]) establishes a homology equivalence of the limit space $ G ( \infty ) $ | ||
| + | and $ ( \Omega ^ {2} S ^ {2} ) _ {0} $( | ||
| + | the subscript indicates that one chooses the component of spheroids of degree 0). As to the unstable homology groups of $ B (n) $, | ||
| + | it has been proved [[#References|[16]]] that they are finite, stabilize at height $ n $ | ||
| + | and satisfy the recurrence relation $ H ^ {i} B (2n + 1) = H ^ {i} B (2n) $. | ||
| + | There is a description of the calculation of these groups [[#References|[17]]]. | ||
==Applications and generalizations.== | ==Applications and generalizations.== | ||
| − | + | 1) A closed braid is a link (an $ n $- | |
| − | 1) A closed braid is a link (an | + | component knot) in $ \mathbf R ^ {3} $ |
| + | each component of which transversally cuts out half-planes bounded by the same straight line: the axis $ l $ | ||
| + | of the closed braid (see Fig. f). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/b017470f.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/b017470f.gif" /> | ||
| Line 132: | Line 420: | ||
Figure: b017470g | Figure: b017470g | ||
| − | A braid | + | A braid $ \omega $ |
| + | generates a closed braid $ \widetilde \omega $( | ||
| + | the closure of $ \omega $) | ||
| + | in the following way. Consider a cylinder with bases on $ P _ {0} $ | ||
| + | and $ P _ {1} $, | ||
| + | the interior of which contains $ \omega $. | ||
| + | Let this cylinder be deformed in $ \mathbf R ^ {3} $ | ||
| + | so that its elements become circles with centres on $ l $, | ||
| + | its bases coincide and each point $ a _ {i} $ | ||
| + | coincides with $ b _ {i} $. | ||
| + | Then $ \widetilde \omega $ | ||
| + | is the union of the strings $ l _ {i} $. | ||
| + | Conversely, every link in $ \mathbf R ^ {3} $ | ||
| + | can be represented by a closed braid. To equivalent braids correspond isotopic links and, moreover, conjugate braids yield isotopic links. The converse is false, since a link may be represented by braids with different numbers of strings. In addition, the braids $ \omega \sigma _ {n - 1 } $ | ||
| + | and $ \omega \sigma _ {n - 1 } ^ {-1} $ | ||
| + | are not conjugate in $ B (n) $, | ||
| + | but they correspond to isotopic links. If two closed braids are equivalent as links, they can be derived from one another by a chain of elementary transformations of two types (see Fig. g). These operations are interpreted in terms of presentations of the link group, thus yielding a reformulation of the isotopy problem for links as a question concerning the system of groups $ B (n) $. | ||
| + | A presentation of the link group of $ \widetilde \omega $ | ||
| + | has the form | ||
| − | + | $$ | |
| + | \{ {y _ {1} \dots y _ {n} } : { | ||
| + | y _ {i} = | ||
| + | A _ {i} y _ {k _ {i} } A _ {i} ^ {-1} } \} | ||
| + | , | ||
| + | $$ | ||
| − | where the relations are defined by braid automorphisms | + | where the relations are defined by braid automorphisms $ b ^ \omega $. |
| + | Conversely, any such relation defines a braid. | ||
| − | 2) If one cuts a surface of genus | + | 2) If one cuts a surface of genus $ g $ |
| + | with $ g $ | ||
| + | non-intersecting cuts so as to obtain a sphere with $ 2g $ | ||
| + | holes, then the homeomorphisms of this sphere with holes that fix points on the edges of the holes define homeomorphisms of the surface which fix the cuts and are themselves defined up to isotopy by the elements of the group $ K (2g) $. | ||
| + | This yields a representation of the braid group in the homotopy group of the surface. Similarly one constructs a representation of $ B (2g) $. | ||
| + | These representations are used in studying Heegaard diagrams of three-dimensional manifolds (cf. [[Three-dimensional manifold|Three-dimensional manifold]]). | ||
| − | 3) By identifying | + | 3) By identifying $ \mathbf R ^ {2} $ |
| + | with the complex plane $ \mathbf C ^ {1} $ | ||
| + | and associating with any unordered set of $ n $ | ||
| + | points in the plane a polynomial of degree $ n $ | ||
| + | having these points as roots, one can identify $ G (n) $ | ||
| + | with the space of polynomials with non-zero discriminants. This has made it possible to obtain several results concerning the non-representability of algebraic functions by superpositions of functions in fewer variables (see [[#References|[16]]]). | ||
| − | 4) Configuration spaces for arbitrary spaces | + | 4) Configuration spaces for arbitrary spaces $ X $ |
| + | are defined in analogy with $ G (n) $ | ||
| + | and $ F (n) $, | ||
| + | with $ \mathbf R ^ {2} $ | ||
| + | replaced by $ X $. | ||
| + | The fundamental groups of these spaces, $ B (X) $ | ||
| + | and $ K (X) $, | ||
| + | are called the braid group of the space $ X $ | ||
| + | and the pure braid group of the space $ X $, | ||
| + | respectively. For a manifold $ M ^ {n} $ | ||
| + | of dimension exceeding 2, $ \pi _ {1} F _ {n} (X) \approx \prod _ {i = 1 } ^ {n} \pi _ {i} M (i) $, | ||
| + | and this group is of no interest. For two-dimensional manifolds, one has a natural imbedding of $ B (n) $ | ||
| + | and $ K (n) $ | ||
| + | into $ B _ {n} (M ^ {2} ) $ | ||
| + | and $ K _ {n} (M ^ {2} ) $ | ||
| + | induced by an imbedding $ \mathbf R ^ {2} \subset M ^ {2} $. | ||
| + | If $ M ^ {2} $ | ||
| + | is neither a sphere nor a projective space, one obtains an exact sequence | ||
| − | + | $$ | |
| + | 1 \rightarrow \pi _ {1} K (2) | ||
| + | \rightarrow ^ { e } \ | ||
| + | \pi _ {1} K _ {n} (M ^ {2} ) | ||
| + | \rightarrow \prod _ {i = 1 } ^ { n } | ||
| + | \pi _ {i} M _ {(i)} ^ {2} ; | ||
| + | $$ | ||
| − | for the sphere, the homomorphism | + | for the sphere, the homomorphism $ e $ |
| + | is an epimorphism, obtained by adding to (1) the single relation | ||
| − | + | $$ | |
| + | \sigma _ {s} \dots | ||
| + | \sigma _ {n - 2 } | ||
| + | \sigma _ {n - 1 } ^ {2} | ||
| + | \sigma _ {n - 2 } \dots | ||
| + | \sigma _ {1} = 1. | ||
| + | $$ | ||
| − | 5) If | + | 5) If $ p: X \rightarrow Y $ |
| + | is a $ k $- | ||
| + | sheeted covering, then $ p ^ {-1} \alpha $, | ||
| + | where $ \alpha $ | ||
| + | is a loop in $ Y $, | ||
| + | is a loop in the configuration space $ X $, | ||
| + | and this defines a homomorphism $ \pi _ {1} Y \rightarrow B _ {k} (X) $ | ||
| + | which strengthens the monodromy of the covering and has applications in algebraic geometry. | ||
| − | 6) Let | + | 6) Let $ V ^ {\mathbf C } $ |
| + | be the complexification of a real vector space $ V $ | ||
| + | and let $ W $ | ||
| + | be a finite irreducible group generated by reflections acting in $ V $( | ||
| + | hence also in $ V ^ {\mathbf C } $). | ||
| + | Let $ s _ {i} $ | ||
| + | be generating reflections in the planes $ P _ {i} \subset V $ | ||
| + | and let $ D $ | ||
| + | be their union. Finally, let $ V ^ {\mathbf C } /D = Y _ {W} $ | ||
| + | and let $ X _ {W} $ | ||
| + | be the quotient space. The groups $ \pi _ {1} Y _ {W} $ | ||
| + | and $ \pi _ {1} X _ {W} $ | ||
| + | are called Brieskorn groups and constitute natural generalizations of $ K (n) $ | ||
| + | and $ B (n) $. | ||
| + | If $ \mathop{\rm ord} (s _ {i} s _ {j} ) = m _ {ij} $, | ||
| + | then $ \pi _ {1} X _ {W} $ | ||
| + | has a presentation of the form | ||
| − | + | $$ | |
| + | \sigma _ {i} \sigma _ {j} \sigma _ {i} \dots = \ | ||
| + | \sigma _ {j} \sigma _ {i} \sigma _ {j} \dots , | ||
| + | $$ | ||
| − | where the number of factors on each side is equal to | + | where the number of factors on each side is equal to $ m _ {ij} $( |
| + | $ \sigma _ {i} $ | ||
| + | here corresponds to a Weyl chamber). It has been proved for these groups that $ X _ {W} $ | ||
| + | and $ Y _ {W} $ | ||
| + | are spaces of type $ K ( \pi , l) $, | ||
| + | and the conjugacy problem has been solved. The spaces $ X _ {W} $ | ||
| + | appear in algebraic geometry as complements to the discriminant of versal deformations of rational singularities (see [[#References|[12]]], [[#References|[13]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Artin, "Theory of braids" ''Ann. of Math.'' , '''48''' (1947) pp. 643–649 {{MR|0019087}} {{ZBL|0030.17703}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.S. Birman, "Braids, links and mapping class groups" , Princeton Univ. Press (1974) {{MR|0375281}} {{ZBL|0305.57013}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> W. Burau, "Ueber Zopfinvarianten" ''Abh. Math. Sem. Univ. Hamburg'' , '''9''' (1932) pp. 117–124 {{MR|}} {{ZBL|0006.03401}} {{ZBL|58.0614.03}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.A. Markov, "Foundations of the algebraic theory of braids" ''Trudy Mat. Inst. Steklov.'' , '''16''' (1945) (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> B. Gassner, "On braid groups" ''Abh. Math. Sem. Univ. Hamburg'' , '''25''' (1961) pp. 10–22 {{MR|0130309}} {{ZBL|0111.03002}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> E. Fadell, L. Neuwirth, "Configuration spaces" ''Math. Scand.'' , '''10''' (1962) pp. 111–118 {{MR|0141127}} {{MR|0141126}} {{ZBL|0136.44104}} {{ZBL|0122.17803}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> F.A. Garside, "The braid group and other groups" ''Quart. J. Math.'' , '''20''' : 4 (1969) pp. 235–254 {{MR|0248801}} {{ZBL|0194.03303}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> D.B. Fuks, "Cohomology of braid groups mod 2" ''Funktional. Anal. i Prilozhen.'' , '''4''' : 2 (1970) pp. 62–73 (In Russian) {{MR|274463}} {{ZBL|}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> V.I. Arnol'd, "On cohomology classes of algebraic functions that are preserved under Tschirnhausen transformations" ''Funktional. Anal. i Prilozhen.'' , '''1''' (1970) pp. 84–85 (In Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> E.A. Gorin, V.Ya. Lin, "Algebraic equations with continuous coefficients and some problems in the theory of braids" ''Mat. Sb.'' , '''78''' (1969) pp. 579–610 (In Russian)</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> V.I. Arnol'd, "On certain topological invariants of algebraic functions" ''Trudy Moskov. Mat. Obshch.'' , '''21''' (1970) pp. 27–46 (In Russian)</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> E. Brieskorn, ''Matematika'' , '''18''' : 3 (1974) pp. 46–59 {{MR|0360085}} {{ZBL|}} </TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> E. Brieskorn, K. Saito, "Artin Gruppen und Coxeter Gruppen" ''Invent. Math.'' , '''17''' (1972) pp. 245–271 {{MR|0323910}} {{ZBL|0243.20037}} </TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> P. Deligne, "Les immeubles des groupes de tresses généralisés" ''Invent. Math.'' , '''17''' : 4 (1972) pp. 273–302 {{MR|0422673}} {{ZBL|0238.20034}} </TD></TR><TR><TD valign="top">[15]</TD> <TD valign="top"> V.Ya. Lin, "Representations of permutation braids" ''Uspekhi Mat. Nauk.'' , '''29''' : 1 (1974) pp. 173–174 (In Russian)</TD></TR><TR><TD valign="top">[16]</TD> <TD valign="top"> V.I. Arnol'd, "The ring of cohomology groups of crossed braids" ''Mat. Zametki'' , '''5''' : 2 (1969) pp. 227–231 (In Russian)</TD></TR><TR><TD valign="top">[17]</TD> <TD valign="top"> V.Ya. Lin, "Artin braids and related groups and spaces" ''Itogi Nauk. i Tekhn. Algebra Topol. Geom.'' , '''17''' (1979) pp. 159–227 (In Russian) {{MR|0584570}} {{ZBL|}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Artin, "Theory of braids" ''Ann. of Math.'' , '''48''' (1947) pp. 643–649 {{MR|0019087}} {{ZBL|0030.17703}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.S. Birman, "Braids, links and mapping class groups" , Princeton Univ. Press (1974) {{MR|0375281}} {{ZBL|0305.57013}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> W. Burau, "Ueber Zopfinvarianten" ''Abh. Math. Sem. Univ. Hamburg'' , '''9''' (1932) pp. 117–124 {{MR|}} {{ZBL|0006.03401}} {{ZBL|58.0614.03}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.A. Markov, "Foundations of the algebraic theory of braids" ''Trudy Mat. Inst. Steklov.'' , '''16''' (1945) (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> B. Gassner, "On braid groups" ''Abh. Math. Sem. Univ. Hamburg'' , '''25''' (1961) pp. 10–22 {{MR|0130309}} {{ZBL|0111.03002}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> E. Fadell, L. Neuwirth, "Configuration spaces" ''Math. Scand.'' , '''10''' (1962) pp. 111–118 {{MR|0141127}} {{MR|0141126}} {{ZBL|0136.44104}} {{ZBL|0122.17803}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> F.A. Garside, "The braid group and other groups" ''Quart. J. Math.'' , '''20''' : 4 (1969) pp. 235–254 {{MR|0248801}} {{ZBL|0194.03303}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> D.B. Fuks, "Cohomology of braid groups mod 2" ''Funktional. Anal. i Prilozhen.'' , '''4''' : 2 (1970) pp. 62–73 (In Russian) {{MR|274463}} {{ZBL|}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> V.I. Arnol'd, "On cohomology classes of algebraic functions that are preserved under Tschirnhausen transformations" ''Funktional. Anal. i Prilozhen.'' , '''1''' (1970) pp. 84–85 (In Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> E.A. Gorin, V.Ya. Lin, "Algebraic equations with continuous coefficients and some problems in the theory of braids" ''Mat. Sb.'' , '''78''' (1969) pp. 579–610 (In Russian)</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> V.I. Arnol'd, "On certain topological invariants of algebraic functions" ''Trudy Moskov. Mat. Obshch.'' , '''21''' (1970) pp. 27–46 (In Russian)</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> E. Brieskorn, ''Matematika'' , '''18''' : 3 (1974) pp. 46–59 {{MR|0360085}} {{ZBL|}} </TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> E. Brieskorn, K. Saito, "Artin Gruppen und Coxeter Gruppen" ''Invent. Math.'' , '''17''' (1972) pp. 245–271 {{MR|0323910}} {{ZBL|0243.20037}} </TD></TR><TR><TD valign="top">[14]</TD> <TD valign="top"> P. Deligne, "Les immeubles des groupes de tresses généralisés" ''Invent. Math.'' , '''17''' : 4 (1972) pp. 273–302 {{MR|0422673}} {{ZBL|0238.20034}} </TD></TR><TR><TD valign="top">[15]</TD> <TD valign="top"> V.Ya. Lin, "Representations of permutation braids" ''Uspekhi Mat. Nauk.'' , '''29''' : 1 (1974) pp. 173–174 (In Russian)</TD></TR><TR><TD valign="top">[16]</TD> <TD valign="top"> V.I. Arnol'd, "The ring of cohomology groups of crossed braids" ''Mat. Zametki'' , '''5''' : 2 (1969) pp. 227–231 (In Russian)</TD></TR><TR><TD valign="top">[17]</TD> <TD valign="top"> V.Ya. Lin, "Artin braids and related groups and spaces" ''Itogi Nauk. i Tekhn. Algebra Topol. Geom.'' , '''17''' (1979) pp. 159–227 (In Russian) {{MR|0584570}} {{ZBL|}} </TD></TR></table> | ||
Revision as of 06:29, 30 May 2020
The branch of topology and algebra concerned with braids, the groups formed by their equivalence classes and various generalizations of these groups [1].
A braid on $ n $ strings is an object consisting of two parallel planes $ P _ {0} $ and $ P _ {1} $ in three-dimensional space $ \mathbf R ^ {3} $, containing two ordered sets of points $ a _ {1} \dots a _ {n} \in P _ {0} $ and $ b _ {1} \dots b _ {n} \in P _ {1} $, and of $ n $ simple non-intersecting arcs $ l _ {1} \dots l _ {n} $, intersecting each parallel plane $ P _ {t} $ between $ P _ {0} $ and $ P _ {1} $ exactly once and joining the points $ \{ a _ {i} \} $ to $ \{ b _ {i} \} $, $ i = 1 \dots n $. It is assumed that the $ a _ {i} $' s lie on a straight line $ L _ {a} $ in $ P _ {0} $ and the $ b _ {i} $' s on a straight line $ L _ {b} $ in $ P _ {1} $ parallel to $ L _ {a} $; moreover, $ b _ {i} $ lies beneath $ a _ {i} $ for each $ i $( see Fig. a). Braids can be represented in the projection on the plane passing through $ L _ {a} $ and $ L _ {b} $; this projection can be brought into general position in such a way that there are only finitely many double points, each two of which lie at different levels, and the intersections are transversal.
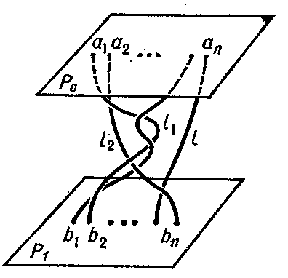
Figure: b017470a
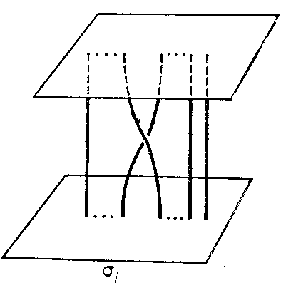
Figure: b017470b
The string $ l _ {i} $ of a braid $ \omega $ joins $ a _ {i} $ to $ b _ {k _ {i} } $ and so defines a permutation
$$ S ^ \omega = \ \left ( \ \begin{array}{ccc} 1 &\dots & n \\ k _ {1} &\dots &k _ {n} \\ \end{array} \ \right ) . $$
If this is the identity permutation, $ \omega $ is called a coloured (or pure) braid. The transposition $ (i i + 1) $ corresponds to a simple braid $ \sigma _ {i} $( see Fig. b).
On the set of all braids on $ n $ strings with fixed $ P _ {0} $, $ P _ {1} $, $ \{ a _ {i} \} $, $ \{ b _ {i} \} $, one introduces the equivalence relation defined by homeomorphisms $ h: \Pi \rightarrow \Pi $, where $ \Pi $ is the region between $ P _ {0} $ and $ P _ {1} $, which reduce to the identity on $ P _ {0} \cup P _ {1} $; it may be assumed that $ h (P _ {t} ) = P _ {t} $. Braids $ \alpha $ and $ \beta $ are equivalent if there exists a homeomorphism with the above properties such that $ h ( \alpha ) = \beta $.
The equivalence classes — which are still called braids — form the braid group $ B (n) $ with respect to the operation defined as follows. Place a copy $ \Pi ^ \prime $ of the domain $ \Pi $ above another copy $ \Pi ^ {\prime\prime} $, in such a way that $ P _ {0} ^ {\prime\prime} $ coincides with $ P _ {1} ^ \prime $, $ a _ {i} ^ {\prime\prime} $ with $ b _ {i} ^ \prime $, and then compress $ \Pi ^ \prime \cup \Pi ^ {\prime\prime} $ to half its "height" . The images of the braids $ \omega ^ \prime \in \Pi ^ \prime $ and $ \omega ^ {\prime\prime} \in \Pi ^ {\prime\prime} $ produce a braid $ \omega ^ \prime \omega ^ {\prime\prime} $, with string $ l _ {i} $ obtained by extending $ l _ {i} ^ \prime $ with $ l _ {k _ {i} } ^ {\prime\prime} $, where $ k _ {i} \in S ^ {\omega ^ \prime (i) } $. The identity braid is the equivalence class containing the braid with $ n $ parallel segments; the inverse $ \omega ^ {-1} $ of a braid $ \omega $ is defined by reflection in the plane $ P _ {1/2} $. For the condition $ \omega \omega ^ {-1} = \epsilon $ see Fig. c.
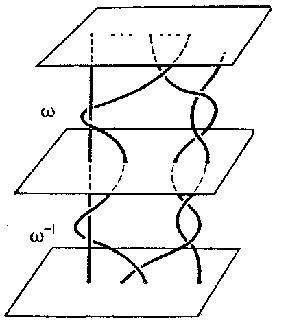
Figure: b017470c
The mapping $ \omega \rightarrow S ^ \omega $ defines an epimorphism of $ B (n) $ onto the group $ S (n) $ of permutations of $ n $ elements, the kernel of this epimorphism is the subgroup $ K (n) $ of all pure braids, so that one has an exact sequence
$$ 1 \rightarrow K (n) \rightarrow B (n) \rightarrow S (n) \rightarrow 1. $$
The braid group $ B (n) $ has two principal interpretations. The first, as a configuration space, is obtained by identifying the planes $ P _ {t} $ via vertical projection onto $ P _ {0} $, under which the images of the points $ a _ {it } = l _ {i} \cap P _ {t} $, considered as $ t $ varies from 0 to 1, form the trace of an isotopy $ \phi _ {t} ^ \omega $ of the set $ \cup a _ {i} $ along $ P _ {0} $; one has $ \phi _ {1} ^ \omega ( \cup a _ {i} ) = \cup a _ {i} $. Consider the space of unordered sequences $ G (n) $ of $ n $ pairwise distinct points of the plane; then each braid corresponds in one-to-one fashion to a class of homotopy loops in this space, and one has an isomorphism
$$ \beta : B (n) \rightarrow \ \pi _ {1} G (n). $$
For pure braids one has an analogously constructed isomorphism
$$ \alpha : K (n) \rightarrow \ \pi _ {1} F (n), $$
where $ F (n) $ is the space of ordered sequences of $ n $ distinct points of the plane, so that $ K (n) $ can be identified with the subgroup corresponding to the covering
$$ p: F (n) \rightarrow G (n) = \ F (n) / S (n). $$
The second interpretation, as a homeotopy group, is obtained by extending the isotopy $ \phi _ {t} ^ \omega $ to an isotopy $ {\widetilde \phi } {} _ {t} ^ \omega $ of the plane $ P _ {0} $ that coincides with the identity outside some disc, and such that $ {\widetilde \phi } {} _ {0} ^ \omega = \mathop{\rm id} $. For each $ t $, two such extensions differ by a homeomorphism which is the identity at the points $ a _ {it} $. A braid uniquely determines a component of the space of homeomorphisms $ Y (n) $ of the plane which map the set $ \cup a _ {i} $ onto itself, and one has an isomorphism
$$ \gamma : B (n) \rightarrow \ \pi _ {0} Y (n). $$
To each homeomorphism $ h \in Y $ corresponds an automorphism of the free group of rank $ n: $ $ F _ {n} = \pi _ {1} ( \mathbf R ^ {2} \setminus \cup a _ {i} ) $, defined up to an inner automorphism, which in turn yields a homomorphism $ B (n) \rightarrow \mathop{\rm Out} F _ {n} = \mathop{\rm Aut} F _ {n} / \mathop{\rm Inn} F _ {n} $. The elements of the image are called braid automorphisms of the free group. In particular, corresponding to the braid $ \sigma _ {i} $ one has an automorphism
$$ \overline \sigma \; _ {i} :\ \overline \sigma \; _ {i} (x _ {i} ) = \ x _ {i + 1 } ,\ \ \overline \sigma \; _ {i} (x _ {i + 1 } ) = \ x _ {i + 1 } x _ {i} x _ {i + 1 } ^ {-1} ,\ \ \overline \sigma \; _ {i} (x _ {j} ) = x _ {j} , $$
if $ j \neq i, i + 1 $( $ \{ x _ {i} \} $ is a set of generators of $ F _ {n} $). Any braid automorphism $ \alpha $ possesses the following properties:
$$ \alpha (x _ {i} ) = \ A _ {i} x _ {i} A _ {i} ^ {-1} ,\ \ \alpha \left ( \prod _ {i = 1 } ^ { n } x _ {i} \right ) = \ \prod _ {i = 1 } ^ { n } x _ {i} , $$
up to an inner automorphism (for the meaning of $ A _ {i} $, see below); these properties characterize braid automorphisms.
The braids $ \sigma _ {i} , 1 \leq i \leq n - 1 $, are the generators of the group $ B (n) $, i.e. $ \omega = \sigma _ {k _ {1} } \dots \sigma _ {k _ {m} } $, with
$$ \tag{1 } \left . \begin{array}{ll} \sigma _ {i} \sigma _ {j} = \ \sigma _ {j} \sigma _ {i} & \textrm{ if } | i - j | > 1, \\ \sigma _ {i} \sigma _ {i + 1 } \sigma _ {i} = \ \sigma _ {i + 1 } \sigma _ {i} \sigma _ {i - 1 } , & 1 \leq i \leq n - 2. \\ \end{array} \ \right \} $$
It turns out that (1) is a presentation of $ B (n) $( see Fig. d).
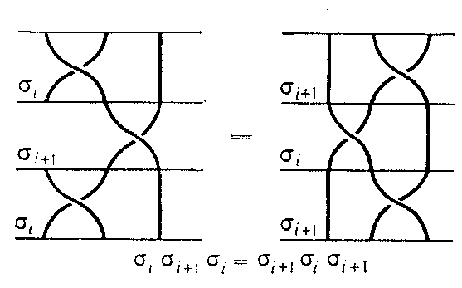
Figure: b017470d
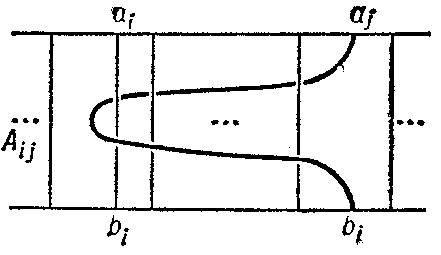
Figure: b017470e
There exists a splitting exact sequence (obtained from the locally trivial fibration $ F (n) \rightarrow F (n - 1) $ with fibre $ \mathbf R ^ {2} \setminus (a _ {1} \dots a _ {n - 1 } ) $):
$$ 1 \rightarrow F _ {n - 1 } \rightarrow K (n) \rightarrow \ K (n - 1) \rightarrow 1, $$
which leads to the normal series
$$ K (n) = \ A _ {n} \supset \dots \supset \ A _ {1} \supset A _ {0} = \ F _ {n - 1 } $$
with free factors $ A _ {i} / A _ {i - 1 } $, where $ A _ {i} $ has a "component" $ U _ {n - i } $ isomorphic to $ K (n - i - 1) $. Each element $ \omega \in B (n) $ can be expressed uniquely in the form
$$ \omega = \ \omega _ {2} \dots \omega _ {n} \pi _ \omega , $$
where $ \pi _ \omega $ is a selected representative for $ S ^ \omega $ in $ B (n) $ and $ \omega _ {i} \in A _ {n - i + 1 } \cap U _ {i} $. The reduction of a braid to this form is known as its dressing. This solves the word (identity) problem in $ B (n) $.
A presentation of $ K (n) $ is as follows: generators (see Fig. e):
$$ A _ {ij} = \ \sigma _ {j - 1 } \sigma _ {j} \sigma _ {j + 1 } \sigma _ {i} ^ {2} \sigma _ {j + 1 } \sigma _ {j} \sigma _ {j - 1 } \in A _ {i} \cap U _ {n - i + 1 } ; $$
relations:
$$ \tag{2 } \left . \begin{array}{ll} A _ {rs} A _ {ij} = A _ {ij} A _ {rs} &\textrm{ if } r \leq s < i < j \\ {} &\textrm{ or } i < r < s < j; \\ A _ {rj} A _ {ij} = A _ {rj} &\textrm{ if } i = s; \\ A _ {ij} A _ {sj} A _ {ij} A _ {ij} = A _ {sj} &\textrm{ if } r = i < j < s; \\ A _ {rj} A _ {sj} A _ {rj} ^ {-1} A _ {sj} ^ {-1} A _ {ij} A _ {rj} A _ {sj} = \ A _ {sj} A _ {rj} &\textrm{ if } r < i < s < j. \\ \end{array} \right \} $$
This presentation may be obtained as a presentation of the kernel of the natural homomorphism into $ S (n) $ of the abstract group $ B (n) $ defined by the presentation (1) with the aid of the Schreier system $ \prod _ {j = 2 } ^ {n} M _ {j} k _ {j} $, $ j \geq k _ {j} \geq n $, where $ M _ {ji} = \sigma _ {j - 1 } \dots \sigma _ {i} $.
The centre of $ B (n) $ is the infinite cyclic group generated by the element $ ( \sigma _ {1} \dots \sigma _ {n} ) ^ {n} $. The commutator group $ B ^ { \prime } (n) $ coincides with $ B ^ { \prime\prime } (n) $ for $ n \geq 5 $; $ B ^ { \prime } (3) $ is isomorphic to the free group of rank 2, and $ B ^ { \prime } (4) $ is isomorphic to semi-direct product of two such groups. The quotient group modulo the commutator subgroup is an infinite cyclic group, generated by the images of $ \sigma _ {i} $. There are no elements of finite order in $ B (n) $. The group $ K (n) $ is mapped onto itself by endomorphisms with non-Abelian image. In particular, $ K (n) \cap B ^ { \prime } (n) $ is a fully-characteristic subgroup of $ B (n) $, and also of $ K (n) $( see [15]).
Solving the conjugacy problem in $ B (n) $ is much more complicated than solving the word problem. There is a unique Garside normal form of a braid, $ \omega = \Delta ^ {m} \Omega $, where $ \Delta = ( \sigma _ {1} {} \dots \sigma _ {n - 1 } ) ( \sigma _ {1} \dots \sigma _ {n - 2 } ) \dots ( \sigma _ {1} \sigma _ {2} ) \sigma _ {1} $ is what is known as a Garside element and $ \Omega $ is a positive braid, i.e. a braid the representation of which in terms of the elements $ \sigma _ {i} $ has positive indices. With any braid $ \omega $ one can associate, using finitely many operations depending on $ i $( conjugation with certain elements, choice of elements of maximum degree, etc.), a certain set of words $ \Sigma ( \omega ) $, from which one selects a word in normal form $ \Delta ^ {+} T $ with minimal $ T $. This is a so-called upper form of the braid $ \omega $. It turns out that two braids are conjugate if and only if they have a same upper form (see [7]).
The Burau representation of the braid group $ B (n) $ in the group of matrices over the ring of polynomials in one variable with integer coefficients is defined by the correspondence
$$ b ( \omega ): \sigma _ {i} \rightarrow \ \left \| \begin{array}{cccc} I _ {i - 1 } & 0 & 0 & 0 \\ 0 &i - t & t & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 &I _ {n - k - 1 } \\ \end{array} \ \right \| , $$
where $ I _ {k} $ is the identity matrix of order $ k $. The matrix $ b ( \omega ) - I _ {n} $ is the reduced Alexander matrix (see Alexander invariants) of the link obtained by closing the braid $ \omega $( see below). For a pure braid one obtains the full Alexander matrix from the analogous Gassner matrix. The problem of whether these representations are faithful is still (1982) unsolved (see [2]).
The fact that the spaces $ F (n) $ and $ G (n) $ are aspherical makes it possible to evaluate the homology of braid groups.
The homology of $ K (n) $( see [16]). Homologically, $ K (n) $ coincides with the product of unions of circles in which the number of circles runs from one through $ n - 1 $. The homology ring is isomorphic to the exterior graded ring generated by the one-dimensional elements $ \omega _ {ij} = \omega _ {ji} $, $ 1 \leq i \leq j \leq n $, with relations
$$ \omega _ {kl} \omega _ {lm} + \omega _ {lm} \omega _ {mk} + \omega _ {mk} \omega _ {kl} = 0. $$
As $ \omega _ {kl} $ one can take the forms
$$ \frac{1}{2 \pi i } \frac{dz _ {k} - dz _ {l} }{z _ {k} - z _ {l} } , $$
corresponding to passage along the diagonals $ z _ {k} = z _ {l} $.
The homology of $ B (n) $( see [8], [12]). The homomorphism $ B (n) \rightarrow S (n) $ can be extended to an imbedding $ S (n) \rightarrow O (n) $; the induced homomorphism of cohomology spaces $ H ^ {*} (O (n)) \rightarrow H ^ {*} (B (n)) $ is epimorphic, i.e. the cohomology spaces $ \mathop{\rm mod} 2 $ of the group $ B (n) $ generated by the Stiefel–Whitney classes.
There is a natural mapping of $ G (n) $ into $ \Omega ^ {2} S ^ {2} $, the two-fold loop space of $ S ^ {2} $, i.e. the space of spheroids $ S ^ {2} \rightarrow S ^ {2} $( choose small discs about $ n $ points, then map these discs canonically with degree 1 into a sphere, mapping the entire complement onto a point). This mapping (see [14]) establishes a homology equivalence of the limit space $ G ( \infty ) $ and $ ( \Omega ^ {2} S ^ {2} ) _ {0} $( the subscript indicates that one chooses the component of spheroids of degree 0). As to the unstable homology groups of $ B (n) $, it has been proved [16] that they are finite, stabilize at height $ n $ and satisfy the recurrence relation $ H ^ {i} B (2n + 1) = H ^ {i} B (2n) $. There is a description of the calculation of these groups [17].
Applications and generalizations.
1) A closed braid is a link (an $ n $- component knot) in $ \mathbf R ^ {3} $ each component of which transversally cuts out half-planes bounded by the same straight line: the axis $ l $ of the closed braid (see Fig. f).
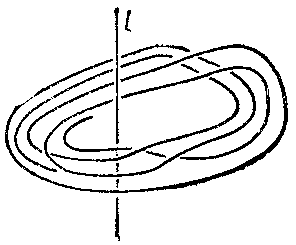
Figure: b017470f
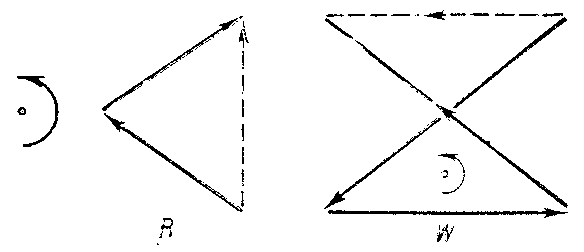
Figure: b017470g
A braid $ \omega $ generates a closed braid $ \widetilde \omega $( the closure of $ \omega $) in the following way. Consider a cylinder with bases on $ P _ {0} $ and $ P _ {1} $, the interior of which contains $ \omega $. Let this cylinder be deformed in $ \mathbf R ^ {3} $ so that its elements become circles with centres on $ l $, its bases coincide and each point $ a _ {i} $ coincides with $ b _ {i} $. Then $ \widetilde \omega $ is the union of the strings $ l _ {i} $. Conversely, every link in $ \mathbf R ^ {3} $ can be represented by a closed braid. To equivalent braids correspond isotopic links and, moreover, conjugate braids yield isotopic links. The converse is false, since a link may be represented by braids with different numbers of strings. In addition, the braids $ \omega \sigma _ {n - 1 } $ and $ \omega \sigma _ {n - 1 } ^ {-1} $ are not conjugate in $ B (n) $, but they correspond to isotopic links. If two closed braids are equivalent as links, they can be derived from one another by a chain of elementary transformations of two types (see Fig. g). These operations are interpreted in terms of presentations of the link group, thus yielding a reformulation of the isotopy problem for links as a question concerning the system of groups $ B (n) $. A presentation of the link group of $ \widetilde \omega $ has the form
$$ \{ {y _ {1} \dots y _ {n} } : { y _ {i} = A _ {i} y _ {k _ {i} } A _ {i} ^ {-1} } \} , $$
where the relations are defined by braid automorphisms $ b ^ \omega $. Conversely, any such relation defines a braid.
2) If one cuts a surface of genus $ g $ with $ g $ non-intersecting cuts so as to obtain a sphere with $ 2g $ holes, then the homeomorphisms of this sphere with holes that fix points on the edges of the holes define homeomorphisms of the surface which fix the cuts and are themselves defined up to isotopy by the elements of the group $ K (2g) $. This yields a representation of the braid group in the homotopy group of the surface. Similarly one constructs a representation of $ B (2g) $. These representations are used in studying Heegaard diagrams of three-dimensional manifolds (cf. Three-dimensional manifold).
3) By identifying $ \mathbf R ^ {2} $ with the complex plane $ \mathbf C ^ {1} $ and associating with any unordered set of $ n $ points in the plane a polynomial of degree $ n $ having these points as roots, one can identify $ G (n) $ with the space of polynomials with non-zero discriminants. This has made it possible to obtain several results concerning the non-representability of algebraic functions by superpositions of functions in fewer variables (see [16]).
4) Configuration spaces for arbitrary spaces $ X $ are defined in analogy with $ G (n) $ and $ F (n) $, with $ \mathbf R ^ {2} $ replaced by $ X $. The fundamental groups of these spaces, $ B (X) $ and $ K (X) $, are called the braid group of the space $ X $ and the pure braid group of the space $ X $, respectively. For a manifold $ M ^ {n} $ of dimension exceeding 2, $ \pi _ {1} F _ {n} (X) \approx \prod _ {i = 1 } ^ {n} \pi _ {i} M (i) $, and this group is of no interest. For two-dimensional manifolds, one has a natural imbedding of $ B (n) $ and $ K (n) $ into $ B _ {n} (M ^ {2} ) $ and $ K _ {n} (M ^ {2} ) $ induced by an imbedding $ \mathbf R ^ {2} \subset M ^ {2} $. If $ M ^ {2} $ is neither a sphere nor a projective space, one obtains an exact sequence
$$ 1 \rightarrow \pi _ {1} K (2) \rightarrow ^ { e } \ \pi _ {1} K _ {n} (M ^ {2} ) \rightarrow \prod _ {i = 1 } ^ { n } \pi _ {i} M _ {(i)} ^ {2} ; $$
for the sphere, the homomorphism $ e $ is an epimorphism, obtained by adding to (1) the single relation
$$ \sigma _ {s} \dots \sigma _ {n - 2 } \sigma _ {n - 1 } ^ {2} \sigma _ {n - 2 } \dots \sigma _ {1} = 1. $$
5) If $ p: X \rightarrow Y $ is a $ k $- sheeted covering, then $ p ^ {-1} \alpha $, where $ \alpha $ is a loop in $ Y $, is a loop in the configuration space $ X $, and this defines a homomorphism $ \pi _ {1} Y \rightarrow B _ {k} (X) $ which strengthens the monodromy of the covering and has applications in algebraic geometry.
6) Let $ V ^ {\mathbf C } $ be the complexification of a real vector space $ V $ and let $ W $ be a finite irreducible group generated by reflections acting in $ V $( hence also in $ V ^ {\mathbf C } $). Let $ s _ {i} $ be generating reflections in the planes $ P _ {i} \subset V $ and let $ D $ be their union. Finally, let $ V ^ {\mathbf C } /D = Y _ {W} $ and let $ X _ {W} $ be the quotient space. The groups $ \pi _ {1} Y _ {W} $ and $ \pi _ {1} X _ {W} $ are called Brieskorn groups and constitute natural generalizations of $ K (n) $ and $ B (n) $. If $ \mathop{\rm ord} (s _ {i} s _ {j} ) = m _ {ij} $, then $ \pi _ {1} X _ {W} $ has a presentation of the form
$$ \sigma _ {i} \sigma _ {j} \sigma _ {i} \dots = \ \sigma _ {j} \sigma _ {i} \sigma _ {j} \dots , $$
where the number of factors on each side is equal to $ m _ {ij} $( $ \sigma _ {i} $ here corresponds to a Weyl chamber). It has been proved for these groups that $ X _ {W} $ and $ Y _ {W} $ are spaces of type $ K ( \pi , l) $, and the conjugacy problem has been solved. The spaces $ X _ {W} $ appear in algebraic geometry as complements to the discriminant of versal deformations of rational singularities (see [12], [13]).
References
| [1] | E. Artin, "Theory of braids" Ann. of Math. , 48 (1947) pp. 643–649 MR0019087 Zbl 0030.17703 |
| [2] | J.S. Birman, "Braids, links and mapping class groups" , Princeton Univ. Press (1974) MR0375281 Zbl 0305.57013 |
| [3] | W. Burau, "Ueber Zopfinvarianten" Abh. Math. Sem. Univ. Hamburg , 9 (1932) pp. 117–124 Zbl 0006.03401 Zbl 58.0614.03 |
| [4] | A.A. Markov, "Foundations of the algebraic theory of braids" Trudy Mat. Inst. Steklov. , 16 (1945) (In Russian) |
| [5] | B. Gassner, "On braid groups" Abh. Math. Sem. Univ. Hamburg , 25 (1961) pp. 10–22 MR0130309 Zbl 0111.03002 |
| [6] | E. Fadell, L. Neuwirth, "Configuration spaces" Math. Scand. , 10 (1962) pp. 111–118 MR0141127 MR0141126 Zbl 0136.44104 Zbl 0122.17803 |
| [7] | F.A. Garside, "The braid group and other groups" Quart. J. Math. , 20 : 4 (1969) pp. 235–254 MR0248801 Zbl 0194.03303 |
| [8] | D.B. Fuks, "Cohomology of braid groups mod 2" Funktional. Anal. i Prilozhen. , 4 : 2 (1970) pp. 62–73 (In Russian) MR274463 |
| [9] | V.I. Arnol'd, "On cohomology classes of algebraic functions that are preserved under Tschirnhausen transformations" Funktional. Anal. i Prilozhen. , 1 (1970) pp. 84–85 (In Russian) |
| [10] | E.A. Gorin, V.Ya. Lin, "Algebraic equations with continuous coefficients and some problems in the theory of braids" Mat. Sb. , 78 (1969) pp. 579–610 (In Russian) |
| [11] | V.I. Arnol'd, "On certain topological invariants of algebraic functions" Trudy Moskov. Mat. Obshch. , 21 (1970) pp. 27–46 (In Russian) |
| [12] | E. Brieskorn, Matematika , 18 : 3 (1974) pp. 46–59 MR0360085 |
| [13] | E. Brieskorn, K. Saito, "Artin Gruppen und Coxeter Gruppen" Invent. Math. , 17 (1972) pp. 245–271 MR0323910 Zbl 0243.20037 |
| [14] | P. Deligne, "Les immeubles des groupes de tresses généralisés" Invent. Math. , 17 : 4 (1972) pp. 273–302 MR0422673 Zbl 0238.20034 |
| [15] | V.Ya. Lin, "Representations of permutation braids" Uspekhi Mat. Nauk. , 29 : 1 (1974) pp. 173–174 (In Russian) |
| [16] | V.I. Arnol'd, "The ring of cohomology groups of crossed braids" Mat. Zametki , 5 : 2 (1969) pp. 227–231 (In Russian) |
| [17] | V.Ya. Lin, "Artin braids and related groups and spaces" Itogi Nauk. i Tekhn. Algebra Topol. Geom. , 17 (1979) pp. 159–227 (In Russian) MR0584570 |
Braid theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Braid_theory&oldid=46145