Difference between revisions of "Bott periodicity theorem"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | b0172201.png | ||
| + | $#A+1 = 31 n = 3 | ||
| + | $#C+1 = 31 : ~/encyclopedia/old_files/data/B017/B.0107220 Bott periodicity theorem | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A fundamental theorem in [[K-theory| $ K $- | |
| + | theory]] which, in its simplest form, states that for any (compact) space $ X $ | ||
| + | there exists an isomorphism between the rings $ K(X) \otimes K(S ^ {2} ) $ | ||
| + | and $ K(X \times S ^ {2} ) $. | ||
| + | More generally, if $ L $ | ||
| + | is a complex vector bundle over $ X $ | ||
| + | and $ P(L \oplus 1) $ | ||
| + | is the projectivization of $ L \oplus 1 $, | ||
| + | then the ring $ K(P(L \oplus 1)) $ | ||
| + | is a $ K(X) $- | ||
| + | algebra with one generator $ [H] $ | ||
| + | and a unique relation $ ([H] - [1])([L][H] - [1]) = 0 $, | ||
| + | where $ [E] $ | ||
| + | is the image of a vector bundle $ E $ | ||
| + | in $ K(X) $ | ||
| + | and $ H ^ {-1} $ | ||
| + | is the Hopf fibration over $ P(L \oplus 1) $. | ||
| + | This fact is equivalent to the existence of a Thom isomorphism in $ K $- | ||
| + | theory for complex vector bundles. In particular, $ P(1 \oplus 1) = X \times S ^ {2} $. | ||
| + | Bott's periodicity theorem was first demonstrated by R. Bott [[#References|[1]]] using Morse theory, and was then re-formulated in terms of $ K $- | ||
| + | theory [[#References|[6]]]; an analogous theorem has also been demonstrated for real fibre bundles. | ||
| + | |||
| + | Bott's periodicity theorem establishes the property of the stable homotopy type of the unitary group $ U $, | ||
| + | consisting in the fact that $ {\Omega ^ {2} } U \sim U $, | ||
| + | where $ \Omega X $ | ||
| + | is the space of loops on $ X $, | ||
| + | and $ \sim $ | ||
| + | is weak homotopy equivalence, in particular $ \pi _ {i} (U) = \pi _ {i+2} (U) $ | ||
| + | for $ i = 0, 1 \dots $ | ||
| + | where $ \pi _ {i} $ | ||
| + | is the $ i $- | ||
| + | th homotopy group. Similarly, for the orthogonal group $ O $: | ||
| + | |||
| + | $$ | ||
| + | \Omega ^ {8} | ||
| + | O \sim O,\ \ | ||
| + | \pi _ {i} (O) = \pi _ {i+ 8 } | ||
| + | (O). | ||
| + | $$ | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> R. Bott, "The stable homotopy of the classical groups" ''Ann. of Math. (2)'' , '''70''' : 2 (1959) pp. 313–337 {{MR|0110104}} {{ZBL|0129.15601}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.W. Milnor, "Morse theory" , Princeton Univ. Press (1963) {{MR|0163331}} {{ZBL|0108.10401}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M.F. Atiyah, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017220/b01722032.png" />-theory: lectures" , Benjamin (1967) {{MR|224083}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) {{MR|0229247}} {{ZBL|0144.44804}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J.C. Moore, "On the periodicity theorem for complex vector bundles" , ''Sem. H. Cartan'' (1959–1960)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M.F. Atiyah, R. Bott, "On the periodicity theorem for complex vector bundles" ''Acta Math.'' , '''112''' (1964) pp. 229–247 {{MR|0178470}} {{ZBL|0131.38201}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> R. Bott, "The stable homotopy of the classical groups" ''Ann. of Math. (2)'' , '''70''' : 2 (1959) pp. 313–337 {{MR|0110104}} {{ZBL|0129.15601}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.W. Milnor, "Morse theory" , Princeton Univ. Press (1963) {{MR|0163331}} {{ZBL|0108.10401}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> M.F. Atiyah, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017220/b01722032.png" />-theory: lectures" , Benjamin (1967) {{MR|224083}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) {{MR|0229247}} {{ZBL|0144.44804}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> J.C. Moore, "On the periodicity theorem for complex vector bundles" , ''Sem. H. Cartan'' (1959–1960)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M.F. Atiyah, R. Bott, "On the periodicity theorem for complex vector bundles" ''Acta Math.'' , '''112''' (1964) pp. 229–247 {{MR|0178470}} {{ZBL|0131.38201}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Bott, "Lectures on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017220/b01722033.png" />" , Benjamin (1969) {{MR|0258020}} {{ZBL|0194.23904}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Karoubi, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017220/b01722034.png" />-theory" , Springer (1978) {{MR|0488029}} {{ZBL|0382.55002}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Bott, "Lectures on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017220/b01722033.png" />" , Benjamin (1969) {{MR|0258020}} {{ZBL|0194.23904}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Karoubi, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017220/b01722034.png" />-theory" , Springer (1978) {{MR|0488029}} {{ZBL|0382.55002}} </TD></TR></table> | ||
Revision as of 06:28, 30 May 2020
A fundamental theorem in $ K $-
theory which, in its simplest form, states that for any (compact) space $ X $
there exists an isomorphism between the rings $ K(X) \otimes K(S ^ {2} ) $
and $ K(X \times S ^ {2} ) $.
More generally, if $ L $
is a complex vector bundle over $ X $
and $ P(L \oplus 1) $
is the projectivization of $ L \oplus 1 $,
then the ring $ K(P(L \oplus 1)) $
is a $ K(X) $-
algebra with one generator $ [H] $
and a unique relation $ ([H] - [1])([L][H] - [1]) = 0 $,
where $ [E] $
is the image of a vector bundle $ E $
in $ K(X) $
and $ H ^ {-1} $
is the Hopf fibration over $ P(L \oplus 1) $.
This fact is equivalent to the existence of a Thom isomorphism in $ K $-
theory for complex vector bundles. In particular, $ P(1 \oplus 1) = X \times S ^ {2} $.
Bott's periodicity theorem was first demonstrated by R. Bott [1] using Morse theory, and was then re-formulated in terms of $ K $-
theory [6]; an analogous theorem has also been demonstrated for real fibre bundles.
Bott's periodicity theorem establishes the property of the stable homotopy type of the unitary group $ U $, consisting in the fact that $ {\Omega ^ {2} } U \sim U $, where $ \Omega X $ is the space of loops on $ X $, and $ \sim $ is weak homotopy equivalence, in particular $ \pi _ {i} (U) = \pi _ {i+2} (U) $ for $ i = 0, 1 \dots $ where $ \pi _ {i} $ is the $ i $- th homotopy group. Similarly, for the orthogonal group $ O $:
$$ \Omega ^ {8} O \sim O,\ \ \pi _ {i} (O) = \pi _ {i+ 8 } (O). $$
References
| [1] | R. Bott, "The stable homotopy of the classical groups" Ann. of Math. (2) , 70 : 2 (1959) pp. 313–337 MR0110104 Zbl 0129.15601 |
| [2] | J.W. Milnor, "Morse theory" , Princeton Univ. Press (1963) MR0163331 Zbl 0108.10401 |
| [3] | M.F. Atiyah, "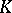 -theory: lectures" , Benjamin (1967) MR224083 -theory: lectures" , Benjamin (1967) MR224083 |
| [4] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) MR0229247 Zbl 0144.44804 |
| [5] | J.C. Moore, "On the periodicity theorem for complex vector bundles" , Sem. H. Cartan (1959–1960) |
| [6] | M.F. Atiyah, R. Bott, "On the periodicity theorem for complex vector bundles" Acta Math. , 112 (1964) pp. 229–247 MR0178470 Zbl 0131.38201 |
Comments
References
| [a1] | R. Bott, "Lectures on 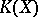 " , Benjamin (1969) MR0258020 Zbl 0194.23904 " , Benjamin (1969) MR0258020 Zbl 0194.23904 |
| [a2] | M. Karoubi, " -theory" , Springer (1978) MR0488029 Zbl 0382.55002 -theory" , Springer (1978) MR0488029 Zbl 0382.55002 |
Bott periodicity theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bott_periodicity_theorem&oldid=46124