Difference between revisions of "Blaschke product"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | b0166301.png | ||
| + | $#A+1 = 45 n = 3 | ||
| + | $#C+1 = 45 : ~/encyclopedia/old_files/data/B016/B.0106630 Blaschke product, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''Blaschke function'' | ''Blaschke function'' | ||
| − | A regular analytic function of a complex variable | + | A regular analytic function of a complex variable $ z $, |
| + | defined in the unit disc $ K = \{ {z } : {| z | < 1 } \} $ | ||
| + | by the finite or infinite product | ||
| + | |||
| + | $$ \tag{* } | ||
| + | B(z) = z ^ {n} | ||
| + | \prod _ { k } | ||
| + | |||
| + | \frac{| a _ {k} | }{a _ {k} } | ||
| + | |||
| + | \frac{a _ {k} -z }{1- \overline{a}\; _ {k} z } | ||
| + | , | ||
| + | $$ | ||
| + | |||
| + | where $ n $ | ||
| + | is a non-negative integer, and $ \{ a _ {k} \} $, | ||
| + | $ k = 1, 2 \dots $ | ||
| + | is a sequence of points $ a _ {k} \in K \setminus \{ 0 \} $ | ||
| + | such that the product on the right-hand side of (*) converges (the convergence condition is necessary only for an infinite product). The Blaschke product was introduced by W. Blaschke [[#References|[1]]], who proved the following theorem: A sequence $ \{ a _ {k} \} $ | ||
| + | of points $ a _ {k} \in K \setminus \{ 0 \} $ | ||
| + | defines a function of the type (*) if and only if the series $ \sum _ {k} (1 - | a _ {k} | ) $ | ||
| + | is convergent. Each factor of the form | ||
| − | + | $$ | |
| + | b _ {k} (z) = \ | ||
| − | + | \frac{| a _ {k} | }{a _ {k} } | |
| − | + | \frac{a _ {k} -z }{1- \overline{a}\; _ {k} z } | |
| + | , | ||
| + | $$ | ||
| − | called the Blaschke factor for | + | called the Blaschke factor for $ a _ {k} $, |
| + | defines a univalent conformal mapping of the disc $ K $ | ||
| + | onto itself, which takes $ z = a _ {k} $ | ||
| + | to zero, with the normalization $ b _ {k} (-a _ {k} / | a _ {k} | ) =1 $. | ||
| + | The factors of the form $ b _ {0} (z) = z $ | ||
| + | may be interpreted as Blaschke factors which correspond to the zero $ z = 0 $ | ||
| + | with the normalization $ b _ {0} (1) = 1 $. | ||
| + | The definition of Blaschke factors and Blaschke products is readily carried over to a disc of arbitrary radius, and also to an arbitrary simply-connected domain, which is conformally equivalent to a disc. | ||
| − | The sequence | + | The sequence $ 0 \dots 0, a _ {1} , a _ {2} ,\dots $( |
| + | with $ n $ | ||
| + | zeros), which is usually written out in non-decreasing order of $ | a _ {k} | $, | ||
| + | is the sequence of all zeros of the Blaschke product (*) (each zero is written down as many times as its multiplicity). Thus, Blaschke's theorem describes the sequences of zeros of all possible Blaschke products. The product (*) can be regarded as the simplest bounded holomorphic function in the disc $ K $ | ||
| + | with a prescribed sequence of zeros. It converges absolutely and uniformly inside $ K $, | ||
| + | represents a bounded holomorphic function $ | B(z) | < 1 $ | ||
| + | in $ K $, | ||
| + | with angular boundary values of modulus one almost everywhere on $ \partial K $. | ||
| + | A necessary and sufficient condition for a bounded holomorphic function $ f(z) $ | ||
| + | in $ K $, | ||
| + | $ | f(z) | < 1 $, | ||
| + | to be a Blaschke product, is | ||
| − | + | $$ | |
| + | \lim\limits _ {r \rightarrow 1 } \ | ||
| + | \int\limits _ { 0 } ^ { {2 } \pi } | ||
| + | \mathop{\rm ln} | f (re ^ {i \theta } ) | | ||
| + | d \theta = 0. | ||
| + | $$ | ||
| − | Blaschke products may be used to give a product representation of important classes of holomorphic functions in the unit disc | + | Blaschke products may be used to give a product representation of important classes of holomorphic functions in the unit disc $ K $. |
| + | Thus, a proof was given for the following theorem of Blaschke: A sequence $ \{ a _ {k} \} $ | ||
| + | of points in the disc $ K $ | ||
| + | is the sequence of all zeros of some bounded holomorphic function $ f(z) $, | ||
| + | $ | f(z) | < 1 $, | ||
| + | in $ K $ | ||
| + | if and only if the series $ \sum _ {k} (1 - | a _ {k} | ) $ | ||
| + | is convergent. Moreover, $ f(z) $ | ||
| + | can be represented as a product | ||
| − | + | $$ | |
| + | f(z) = B _ {f} (z) g (z), | ||
| + | $$ | ||
| − | where | + | where $ B _ {f} (z) $ |
| + | is the Blaschke product constructed with the zeros $ \{ a _ {k} \} $ | ||
| + | of the function $ f(z) $, | ||
| + | while $ g(z) $ | ||
| + | is a zero-free holomorphic function in $ K $, | ||
| + | $ | g(z) | \leq 1 $, | ||
| + | which can be represented relatively simply using an integral formula. Apart from the bounded functions, similar product representations may be constructed for functions of bounded form and for [[Hardy classes|Hardy classes]] [[#References|[2]]]–[[#References|[4]]] (cf. [[Function of bounded form|Function of bounded form]]). | ||
The above theory was considerably generalized by M.M. Dzhrbashyan [[#References|[5]]], [[#References|[6]]], who constructed infinite products of a more general nature, which are suitable for the factorization of much larger classes of meromorphic functions. A solution was also found for the problem of constructing analogues of Blaschke products and Blaschke's theorem for doubly-connected domains [[#References|[7]]] and, in general, finitely-connected [[#References|[8]]] domains. The solution of the problem of constructing suitable analogues of the Blaschke product for holomorphic functions of several complex variables is rendered very difficult by the fact that the zeros of such functions cannot be isolated. | The above theory was considerably generalized by M.M. Dzhrbashyan [[#References|[5]]], [[#References|[6]]], who constructed infinite products of a more general nature, which are suitable for the factorization of much larger classes of meromorphic functions. A solution was also found for the problem of constructing analogues of Blaschke products and Blaschke's theorem for doubly-connected domains [[#References|[7]]] and, in general, finitely-connected [[#References|[8]]] domains. The solution of the problem of constructing suitable analogues of the Blaschke product for holomorphic functions of several complex variables is rendered very difficult by the fact that the zeros of such functions cannot be isolated. | ||
| Line 25: | Line 100: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> W. Blaschke, "Eine Erweiterung des Satzes von Vitali über Folgen analytischer Funktionen" ''Berichte Math.-Phys. Kl., Sächs. Gesell. der Wiss. Leipzig'' , '''67''' (1915) pp. 194–200</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 1;6</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M.M. Dzhrbashyan, "Integral transforms and representation of functions in the complex domain" , Moscow (1966) (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M.M. Dzhrbashyan, "The theory of factorization and boundary properties of functions meromorphic in a disc" ''Russian Math. Surveys'' , '''28''' : 4 (1973) pp. 1–12 ''Uspekhi Mat. Nauk'' , '''28''' : 4 (1973) pp. 3–14</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> S.A. Kas'yanyuk, "On functions of classes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016630/b01663046.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016630/b01663047.png" /> in an annulus" ''Mat. Sb.'' , '''42 (84)''' : 3 (1957) pp. 301–326</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> P.M. Tamrazov, "Conformal-metric theory of doubly connected domains and the generalized Blaschke product" ''Soviet Math. Dokl.'' , '''6''' : 2 (1965) pp. 432–435 ''Dokl. Akad. Nauk SSSR'' , '''161''' : 2 (1965) pp. 308–311</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> W. Blaschke, "Eine Erweiterung des Satzes von Vitali über Folgen analytischer Funktionen" ''Berichte Math.-Phys. Kl., Sächs. Gesell. der Wiss. Leipzig'' , '''67''' (1915) pp. 194–200</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 1;6</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> M.M. Dzhrbashyan, "Integral transforms and representation of functions in the complex domain" , Moscow (1966) (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M.M. Dzhrbashyan, "The theory of factorization and boundary properties of functions meromorphic in a disc" ''Russian Math. Surveys'' , '''28''' : 4 (1973) pp. 1–12 ''Uspekhi Mat. Nauk'' , '''28''' : 4 (1973) pp. 3–14</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> S.A. Kas'yanyuk, "On functions of classes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016630/b01663046.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016630/b01663047.png" /> in an annulus" ''Mat. Sb.'' , '''42 (84)''' : 3 (1957) pp. 301–326</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> P.M. Tamrazov, "Conformal-metric theory of doubly connected domains and the generalized Blaschke product" ''Soviet Math. Dokl.'' , '''6''' : 2 (1965) pp. 432–435 ''Dokl. Akad. Nauk SSSR'' , '''161''' : 2 (1965) pp. 308–311</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Revision as of 10:59, 29 May 2020
Blaschke function
A regular analytic function of a complex variable $ z $, defined in the unit disc $ K = \{ {z } : {| z | < 1 } \} $ by the finite or infinite product
$$ \tag{* } B(z) = z ^ {n} \prod _ { k } \frac{| a _ {k} | }{a _ {k} } \frac{a _ {k} -z }{1- \overline{a}\; _ {k} z } , $$
where $ n $ is a non-negative integer, and $ \{ a _ {k} \} $, $ k = 1, 2 \dots $ is a sequence of points $ a _ {k} \in K \setminus \{ 0 \} $ such that the product on the right-hand side of (*) converges (the convergence condition is necessary only for an infinite product). The Blaschke product was introduced by W. Blaschke [1], who proved the following theorem: A sequence $ \{ a _ {k} \} $ of points $ a _ {k} \in K \setminus \{ 0 \} $ defines a function of the type (*) if and only if the series $ \sum _ {k} (1 - | a _ {k} | ) $ is convergent. Each factor of the form
$$ b _ {k} (z) = \ \frac{| a _ {k} | }{a _ {k} } \frac{a _ {k} -z }{1- \overline{a}\; _ {k} z } , $$
called the Blaschke factor for $ a _ {k} $, defines a univalent conformal mapping of the disc $ K $ onto itself, which takes $ z = a _ {k} $ to zero, with the normalization $ b _ {k} (-a _ {k} / | a _ {k} | ) =1 $. The factors of the form $ b _ {0} (z) = z $ may be interpreted as Blaschke factors which correspond to the zero $ z = 0 $ with the normalization $ b _ {0} (1) = 1 $. The definition of Blaschke factors and Blaschke products is readily carried over to a disc of arbitrary radius, and also to an arbitrary simply-connected domain, which is conformally equivalent to a disc.
The sequence $ 0 \dots 0, a _ {1} , a _ {2} ,\dots $( with $ n $ zeros), which is usually written out in non-decreasing order of $ | a _ {k} | $, is the sequence of all zeros of the Blaschke product (*) (each zero is written down as many times as its multiplicity). Thus, Blaschke's theorem describes the sequences of zeros of all possible Blaschke products. The product (*) can be regarded as the simplest bounded holomorphic function in the disc $ K $ with a prescribed sequence of zeros. It converges absolutely and uniformly inside $ K $, represents a bounded holomorphic function $ | B(z) | < 1 $ in $ K $, with angular boundary values of modulus one almost everywhere on $ \partial K $. A necessary and sufficient condition for a bounded holomorphic function $ f(z) $ in $ K $, $ | f(z) | < 1 $, to be a Blaschke product, is
$$ \lim\limits _ {r \rightarrow 1 } \ \int\limits _ { 0 } ^ { {2 } \pi } \mathop{\rm ln} | f (re ^ {i \theta } ) | d \theta = 0. $$
Blaschke products may be used to give a product representation of important classes of holomorphic functions in the unit disc $ K $. Thus, a proof was given for the following theorem of Blaschke: A sequence $ \{ a _ {k} \} $ of points in the disc $ K $ is the sequence of all zeros of some bounded holomorphic function $ f(z) $, $ | f(z) | < 1 $, in $ K $ if and only if the series $ \sum _ {k} (1 - | a _ {k} | ) $ is convergent. Moreover, $ f(z) $ can be represented as a product
$$ f(z) = B _ {f} (z) g (z), $$
where $ B _ {f} (z) $ is the Blaschke product constructed with the zeros $ \{ a _ {k} \} $ of the function $ f(z) $, while $ g(z) $ is a zero-free holomorphic function in $ K $, $ | g(z) | \leq 1 $, which can be represented relatively simply using an integral formula. Apart from the bounded functions, similar product representations may be constructed for functions of bounded form and for Hardy classes [2]–[4] (cf. Function of bounded form).
The above theory was considerably generalized by M.M. Dzhrbashyan [5], [6], who constructed infinite products of a more general nature, which are suitable for the factorization of much larger classes of meromorphic functions. A solution was also found for the problem of constructing analogues of Blaschke products and Blaschke's theorem for doubly-connected domains [7] and, in general, finitely-connected [8] domains. The solution of the problem of constructing suitable analogues of the Blaschke product for holomorphic functions of several complex variables is rendered very difficult by the fact that the zeros of such functions cannot be isolated.
References
| [1] | W. Blaschke, "Eine Erweiterung des Satzes von Vitali über Folgen analytischer Funktionen" Berichte Math.-Phys. Kl., Sächs. Gesell. der Wiss. Leipzig , 67 (1915) pp. 194–200 |
| [2] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [3] | R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German) |
| [4] | E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 1;6 |
| [5] | M.M. Dzhrbashyan, "Integral transforms and representation of functions in the complex domain" , Moscow (1966) (In Russian) |
| [6] | M.M. Dzhrbashyan, "The theory of factorization and boundary properties of functions meromorphic in a disc" Russian Math. Surveys , 28 : 4 (1973) pp. 1–12 Uspekhi Mat. Nauk , 28 : 4 (1973) pp. 3–14 |
| [7] | S.A. Kas'yanyuk, "On functions of classes 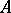 and and 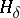 in an annulus" Mat. Sb. , 42 (84) : 3 (1957) pp. 301–326 in an annulus" Mat. Sb. , 42 (84) : 3 (1957) pp. 301–326 |
| [8] | P.M. Tamrazov, "Conformal-metric theory of doubly connected domains and the generalized Blaschke product" Soviet Math. Dokl. , 6 : 2 (1965) pp. 432–435 Dokl. Akad. Nauk SSSR , 161 : 2 (1965) pp. 308–311 |
Comments
Some standard references for Blaschke products and related subjects are [a1], [a2] and [a3].
References
| [a1] | P.L. Duren, "Theory of 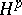 spaces" , Acad. Press (1970) spaces" , Acad. Press (1970) |
| [a2] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1974) pp. 24 |
| [a3] | J.B. Garnett, "Bounded analytic functions" , Acad. Press (1981) pp. 40 |
Blaschke product. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Blaschke_product&oldid=46083