Difference between revisions of "Bernoulli random walk"
(→References: Feller: internal link) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | b0156601.png | ||
| + | $#A+1 = 84 n = 0 | ||
| + | $#C+1 = 84 : ~/encyclopedia/old_files/data/B015/B.0105660 Bernoulli random walk | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
A [[Random walk|random walk]] generated by [[Bernoulli trials|Bernoulli trials]]. The example of a Bernoulli random walk may be used to explain certain basic features of more general random walks. In particular, even in this very simple scheme there appear properties of "randomness" which are intuitively paradoxical. | A [[Random walk|random walk]] generated by [[Bernoulli trials|Bernoulli trials]]. The example of a Bernoulli random walk may be used to explain certain basic features of more general random walks. In particular, even in this very simple scheme there appear properties of "randomness" which are intuitively paradoxical. | ||
| − | Thus, a Bernoulli random walk may be described in the following terms. A particle moves "randomly" along the | + | Thus, a Bernoulli random walk may be described in the following terms. A particle moves "randomly" along the $ x $- |
| + | axis over a lattice of points of the form $ kh $( | ||
| + | $ k $ | ||
| + | is an integer, $ h > 0 $). | ||
| + | The motion begins at the moment $ t=0 $, | ||
| + | and the location of the particle is noted only at discrete moments of time $ 0, \Delta t, 2 \Delta t ,\dots $. | ||
| + | At each step the value of the coordinate of the particle increases or decreases by a magnitude $ h $ | ||
| + | with probabilities $ p $ | ||
| + | and $ q = 1 - p $, | ||
| + | respectively, irrespective of the nature of the previous motion. Thus, shifts in the positive and in the negative directions ( "successes" and "failures" ) are described by a Bernoulli trial scheme with probability of success $ p $. | ||
| + | The Bernoulli random walk is usually represented geometrically: take the $ t $- | ||
| + | axis as the abscissa, and the $ x $- | ||
| + | axis as the ordinate (cf. Fig. a, showing the initial segment of the graph of a random walk of a particle beginning to move from zero). | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/b015660a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/b015660a.gif" /> | ||
| Line 9: | Line 33: | ||
The initial segment of the graph representing the motion of a particle performing a Bernoulli random walk. | The initial segment of the graph representing the motion of a particle performing a Bernoulli random walk. | ||
| − | Let | + | Let $ X _ {j} $ |
| + | be the random variable corresponding to the displacement of the particle in the $ j $- | ||
| + | th step. Then $ X _ {1} , X _ {2} \dots $ | ||
| + | is a sequence of independent random variables. The coordinate of the randomly-moving particle at the moment $ n \Delta t $ | ||
| + | is equal to the sum $ S _ {n} = X _ {1} + \dots + X _ {n} $. | ||
| + | This is why the graph of a Bernoulli random walk is an illustrative representation of the behaviour of the cumulative sums of random variables; moreover, many typical features of the fluctuations are preserved for the sums of much more general random variables as well. This graph also shows the changes in the capital at the disposal of one of the players in the classical ruin problem (the formulas giving the probabilities of numerous events taking place in the course of a Bernoulli random walk were in fact developed in connection with this problem). | ||
A Bernoulli random walk is used in physics as a rough description of one-dimensional diffusion processes (cf. [[Diffusion process|Diffusion process]]) and of the [[Brownian motion|Brownian motion]] of material particles under collisions with molecules. | A Bernoulli random walk is used in physics as a rough description of one-dimensional diffusion processes (cf. [[Diffusion process|Diffusion process]]) and of the [[Brownian motion|Brownian motion]] of material particles under collisions with molecules. | ||
| − | Important facts involved in a Bernoulli random walk will be described below. In so doing, it is assumed that | + | Important facts involved in a Bernoulli random walk will be described below. In so doing, it is assumed that $ \Delta t = 1 $, |
| + | $ h = 1 $. | ||
| − | Probabilities of returning. Let the walk begin from zero. The probability of at least one return to zero then is | + | Probabilities of returning. Let the walk begin from zero. The probability of at least one return to zero then is $ 1 - | p - q | $, |
| + | that is, one in the symmetric case $ p = q = 1/2 $, | ||
| + | and less than one if $ p \neq q $. | ||
| + | In the symmetric case the values of $ \tau _ {1} $( | ||
| + | i.e. the time elapsed until the first return to zero) and $ \tau _ {2} $( | ||
| + | the time between the first and the second return to zero), etc., are independent random variables with an infinite mathematical expectation. The time elapsed until the $ N $- | ||
| + | th return, i.e. the sum $ \tau _ {1} + \dots + \tau _ {N} $, | ||
| + | increases as $ N ^ {2} $, | ||
| + | while the average number $ N _ {2n} $ | ||
| + | of returns during $ 2n $ | ||
| + | steps is given by the formula | ||
| − | + | $$ | |
| + | {\mathsf E} (N _ {2n } ) = \ | ||
| − | + | \frac{2n + 1 }{2 ^ {2n} } | |
| − | + | \left ( | |
| + | \begin{array}{c} | ||
| + | 2n \\ | ||
| + | n | ||
| + | \end{array} | ||
| + | |||
| + | \right ) - 1 | ||
| + | $$ | ||
| + | |||
| + | which increases as $ \sqrt n $: | ||
| + | |||
| + | $$ | ||
| + | {\mathsf E} (N _ {2n} ) \sim 2 | ||
| + | |||
| + | \frac{\sqrt n }{\sqrt \pi } | ||
| + | . | ||
| + | $$ | ||
The consequence is paradoxical: In a symmetric Bernoulli random walk, the intervals ( "waves" ) between the successive returns to zero on the graph are surprisingly long (Fig. b). | The consequence is paradoxical: In a symmetric Bernoulli random walk, the intervals ( "waves" ) between the successive returns to zero on the graph are surprisingly long (Fig. b). | ||
| Line 31: | Line 88: | ||
Graphs of three Bernoulli random walks: each one was observed during 200,000 units of time. | Graphs of three Bernoulli random walks: each one was observed during 200,000 units of time. | ||
| − | Another related feature is that the least probable values of | + | Another related feature is that the least probable values of $ T _ {n} / n $( |
| + | the fraction of time that the graph is above the abscissa) are those close to $ 1/2 $. | ||
| + | More exactly, the following theorem is valid: If $ k \rightarrow \infty $, | ||
| + | $ n - k \rightarrow \infty $, | ||
| + | then the formula | ||
| + | |||
| + | $$ | ||
| + | p _ {2n, 2k } \sim \ | ||
| + | |||
| + | \frac{1}{\pi n \sqrt x(1-x) } | ||
| + | , | ||
| + | $$ | ||
| + | |||
| + | where $ x = x _ {n,k } = k/n $, | ||
| + | gives the probability $ p _ {2n,2k} $ | ||
| + | of the equality $ T _ {2n} = 2k $. | ||
| + | A corollary is the so-called arcsine law: For each $ 0 < \alpha < 1 $ | ||
| + | the probability of the inequality $ T _ {n} / n < \alpha $ | ||
| + | tends to | ||
| + | |||
| + | $$ | ||
| − | + | \frac{1} \pi | |
| + | \int\limits _ { 0 } ^ \alpha | ||
| − | + | \frac{dx}{\sqrt x(1-x) } | |
| + | = \ | ||
| − | + | \frac{2} \pi | |
| + | \mathop{\rm arc} \sin \sqrt \alpha . | ||
| + | $$ | ||
| − | It is possible to prove, starting from this fact, that during 10,000 steps the particle remains on the positive side more than 9930 units of time with a probability | + | It is possible to prove, starting from this fact, that during 10,000 steps the particle remains on the positive side more than 9930 units of time with a probability $ \geq 0.1 $, |
| + | i.e. roughly speaking, such a graph will be observed not less frequently than in one case out of ten (even though this seems absurd at first sight). | ||
| − | Maximum deviation. If | + | Maximum deviation. If $ p > q $ |
| + | or $ p < q $, | ||
| + | the randomly-moving particle will move towards $ + \infty $ | ||
| + | or $ - \infty $ | ||
| + | with probability one. Thus, if $ p < q $, | ||
| + | one defines the random variable | ||
| − | + | $$ | |
| + | M ^ {+} = \max _ {0 \leq j < \infty } \ | ||
| + | S _ {j} , | ||
| + | $$ | ||
| − | and then the probability of | + | and then the probability of $ M ^ {+} = x $ |
| + | is | ||
| − | + | $$ | |
| + | \left ( 1 - | ||
| + | \frac{p}{q} | ||
| + | \right ) | ||
| + | \left ( | ||
| + | \frac{p}{q} | ||
| + | \right ) ^ {x} . | ||
| + | $$ | ||
| − | A bounded Bernoulli random walk. One often considers a Bernoulli random walk in the presence of absorbing or reflecting barriers. For instance, let the walk begin from zero. The presence of an absorbing barrier at a point | + | A bounded Bernoulli random walk. One often considers a Bernoulli random walk in the presence of absorbing or reflecting barriers. For instance, let the walk begin from zero. The presence of an absorbing barrier at a point $ a $ |
| + | is manifested by that, on reaching this point, the particle ceases to move. In the presence of a reflecting barrier at the point $ a = (k + 1/2 ) $, | ||
| + | $ k \geq 0 $ | ||
| + | an integer, the particle will move from $ k $ | ||
| + | to $ k - 1 $ | ||
| + | with probability $ q $, | ||
| + | and will remain in place with probability $ p $. | ||
| + | Finite-difference equations are a principal tool in computing the probabilities of the absorption and of attaining specified points. For instance, let the absorbing barrier be located at the point $ -a $( | ||
| + | $ a > 0 $). | ||
| + | If $ z _ {t,x} $ | ||
| + | is the probability of a particle located at $ x $ | ||
| + | at the moment of time $ t $ | ||
| + | to be absorbed before or at the moment $ n $, | ||
| + | then the following equation is valid | ||
| − | + | $$ | |
| + | z _ {t,x} = \ | ||
| + | q z _ {t+1,x-1} +pz _ {t + 1, x + 1 } ,\ x > - a , | ||
| + | $$ | ||
with the following obvious boundary conditions: | with the following obvious boundary conditions: | ||
| − | + | $$ | |
| + | z _ {t,-a} = 1 ,\ \ | ||
| + | 0 \leq t \leq n , | ||
| + | $$ | ||
| − | + | $$ | |
| + | z _ {n,x} = 0 ,\ x > -a . | ||
| + | $$ | ||
| − | The solution of this problem for | + | The solution of this problem for $ p = q = 1/2 $ |
| + | was known to A. de Moivre and to P. Laplace. The Laplace formula is: | ||
| − | + | $$ \tag{* } | |
| + | z _ {t,x} = 1 - | ||
| + | \frac{2} \pi | ||
| + | |||
| + | \int\limits _ { 0 } ^ { \pi /2 } | ||
| + | |||
| + | \frac{\sin (a+x) \phi }{\sin \phi } | ||
| + | |||
| + | ( \cos \phi ) ^ \nu d \phi , | ||
| + | $$ | ||
where | where | ||
| − | + | $$ | |
| + | \nu = a + x + 2 | ||
| + | \left [ | ||
| + | |||
| + | \frac{n-t-x-a}{2} | ||
| + | |||
| + | \right ] + 1 . | ||
| + | $$ | ||
| + | |||
| + | The transition to diffusion processes. As an example, let $ p = q = 1/2 $, | ||
| + | $ \Delta t = 1/N $, | ||
| + | $ h = 1/ \sqrt N $. | ||
| + | Then, as $ N \rightarrow \infty $, | ||
| + | many probabilities, calculated for a Bernoulli random walk, tend to limits which are equal to the respective probabilities of a Brownian motion. As an example, consider the probability of a particle, which has departed from zero, reaching a barrier located at a point $ \alpha $ | ||
| + | before or at the moment $ T $. | ||
| + | The limit transition from formula (*), for $ n/N = T $, | ||
| + | $ t = 0 $, | ||
| + | $ a/ \sqrt N = \alpha $, | ||
| + | gives the magnitude | ||
| + | |||
| + | $$ | ||
| + | 1 - | ||
| + | \frac{2}{\sqrt {2 \pi } } | ||
| + | |||
| + | \int\limits _ { 0 } ^ { \alpha / \sqrt T } | ||
| + | e ^ {-z ^ {2} /2 } dz = \ | ||
| − | + | \frac{2}{\sqrt {2 \pi } } | |
| − | + | \int\limits _ {\alpha / \sqrt T } ^ \infty | |
| + | e ^ {-z ^ {2} /2 } dz , | ||
| + | $$ | ||
| − | which is equal to the probability that the coordinate | + | which is equal to the probability that the coordinate $ X( \nu ) $ |
| + | of a particle executing a Brownian motion satisfies the inequality | ||
| − | + | $$ | |
| + | \mathop{\rm min} _ {0 \leq \nu \leq T } \ | ||
| + | X( \nu ) \leq - \alpha , | ||
| + | $$ | ||
| − | i.e. to the probability that the particle is absorbed at the barrier | + | i.e. to the probability that the particle is absorbed at the barrier $ - \alpha $. |
| + | For the sake of a more or less complete description of such limit relationships it is expedient to adopt a general standpoint and to consider the transition from the discrete process of "cumulative sums" to a continuous random process (cf. [[Limit theorems|Limit theorems]]). | ||
The scheme of a Bernoulli random walk is very useful in explaining the characteristic features of the behaviour of sums of random variables such as the [[Strong law of large numbers|strong law of large numbers]] and the [[Law of the iterated logarithm|law of the iterated logarithm]]. | The scheme of a Bernoulli random walk is very useful in explaining the characteristic features of the behaviour of sums of random variables such as the [[Strong law of large numbers|strong law of large numbers]] and the [[Law of the iterated logarithm|law of the iterated logarithm]]. | ||
Revision as of 10:58, 29 May 2020
A random walk generated by Bernoulli trials. The example of a Bernoulli random walk may be used to explain certain basic features of more general random walks. In particular, even in this very simple scheme there appear properties of "randomness" which are intuitively paradoxical.
Thus, a Bernoulli random walk may be described in the following terms. A particle moves "randomly" along the $ x $- axis over a lattice of points of the form $ kh $( $ k $ is an integer, $ h > 0 $). The motion begins at the moment $ t=0 $, and the location of the particle is noted only at discrete moments of time $ 0, \Delta t, 2 \Delta t ,\dots $. At each step the value of the coordinate of the particle increases or decreases by a magnitude $ h $ with probabilities $ p $ and $ q = 1 - p $, respectively, irrespective of the nature of the previous motion. Thus, shifts in the positive and in the negative directions ( "successes" and "failures" ) are described by a Bernoulli trial scheme with probability of success $ p $. The Bernoulli random walk is usually represented geometrically: take the $ t $- axis as the abscissa, and the $ x $- axis as the ordinate (cf. Fig. a, showing the initial segment of the graph of a random walk of a particle beginning to move from zero).
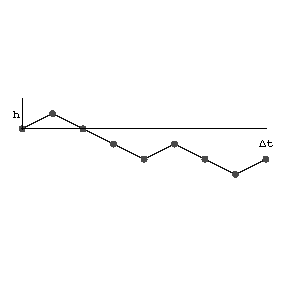
Figure: b015660a
The initial segment of the graph representing the motion of a particle performing a Bernoulli random walk.
Let $ X _ {j} $ be the random variable corresponding to the displacement of the particle in the $ j $- th step. Then $ X _ {1} , X _ {2} \dots $ is a sequence of independent random variables. The coordinate of the randomly-moving particle at the moment $ n \Delta t $ is equal to the sum $ S _ {n} = X _ {1} + \dots + X _ {n} $. This is why the graph of a Bernoulli random walk is an illustrative representation of the behaviour of the cumulative sums of random variables; moreover, many typical features of the fluctuations are preserved for the sums of much more general random variables as well. This graph also shows the changes in the capital at the disposal of one of the players in the classical ruin problem (the formulas giving the probabilities of numerous events taking place in the course of a Bernoulli random walk were in fact developed in connection with this problem).
A Bernoulli random walk is used in physics as a rough description of one-dimensional diffusion processes (cf. Diffusion process) and of the Brownian motion of material particles under collisions with molecules.
Important facts involved in a Bernoulli random walk will be described below. In so doing, it is assumed that $ \Delta t = 1 $, $ h = 1 $.
Probabilities of returning. Let the walk begin from zero. The probability of at least one return to zero then is $ 1 - | p - q | $, that is, one in the symmetric case $ p = q = 1/2 $, and less than one if $ p \neq q $. In the symmetric case the values of $ \tau _ {1} $( i.e. the time elapsed until the first return to zero) and $ \tau _ {2} $( the time between the first and the second return to zero), etc., are independent random variables with an infinite mathematical expectation. The time elapsed until the $ N $- th return, i.e. the sum $ \tau _ {1} + \dots + \tau _ {N} $, increases as $ N ^ {2} $, while the average number $ N _ {2n} $ of returns during $ 2n $ steps is given by the formula
$$ {\mathsf E} (N _ {2n } ) = \ \frac{2n + 1 }{2 ^ {2n} } \left ( \begin{array}{c} 2n \\ n \end{array} \right ) - 1 $$
which increases as $ \sqrt n $:
$$ {\mathsf E} (N _ {2n} ) \sim 2 \frac{\sqrt n }{\sqrt \pi } . $$
The consequence is paradoxical: In a symmetric Bernoulli random walk, the intervals ( "waves" ) between the successive returns to zero on the graph are surprisingly long (Fig. b).
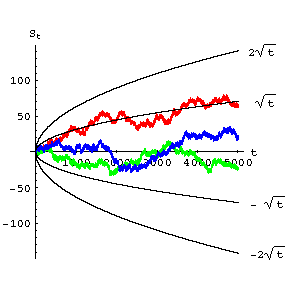
Figure: b015660b
Graphs of three Bernoulli random walks: each one was observed during 200,000 units of time.
Another related feature is that the least probable values of $ T _ {n} / n $( the fraction of time that the graph is above the abscissa) are those close to $ 1/2 $. More exactly, the following theorem is valid: If $ k \rightarrow \infty $, $ n - k \rightarrow \infty $, then the formula
$$ p _ {2n, 2k } \sim \ \frac{1}{\pi n \sqrt x(1-x) } , $$
where $ x = x _ {n,k } = k/n $, gives the probability $ p _ {2n,2k} $ of the equality $ T _ {2n} = 2k $. A corollary is the so-called arcsine law: For each $ 0 < \alpha < 1 $ the probability of the inequality $ T _ {n} / n < \alpha $ tends to
$$ \frac{1} \pi \int\limits _ { 0 } ^ \alpha \frac{dx}{\sqrt x(1-x) } = \ \frac{2} \pi \mathop{\rm arc} \sin \sqrt \alpha . $$
It is possible to prove, starting from this fact, that during 10,000 steps the particle remains on the positive side more than 9930 units of time with a probability $ \geq 0.1 $, i.e. roughly speaking, such a graph will be observed not less frequently than in one case out of ten (even though this seems absurd at first sight).
Maximum deviation. If $ p > q $ or $ p < q $, the randomly-moving particle will move towards $ + \infty $ or $ - \infty $ with probability one. Thus, if $ p < q $, one defines the random variable
$$ M ^ {+} = \max _ {0 \leq j < \infty } \ S _ {j} , $$
and then the probability of $ M ^ {+} = x $ is
$$ \left ( 1 - \frac{p}{q} \right ) \left ( \frac{p}{q} \right ) ^ {x} . $$
A bounded Bernoulli random walk. One often considers a Bernoulli random walk in the presence of absorbing or reflecting barriers. For instance, let the walk begin from zero. The presence of an absorbing barrier at a point $ a $ is manifested by that, on reaching this point, the particle ceases to move. In the presence of a reflecting barrier at the point $ a = (k + 1/2 ) $, $ k \geq 0 $ an integer, the particle will move from $ k $ to $ k - 1 $ with probability $ q $, and will remain in place with probability $ p $. Finite-difference equations are a principal tool in computing the probabilities of the absorption and of attaining specified points. For instance, let the absorbing barrier be located at the point $ -a $( $ a > 0 $). If $ z _ {t,x} $ is the probability of a particle located at $ x $ at the moment of time $ t $ to be absorbed before or at the moment $ n $, then the following equation is valid
$$ z _ {t,x} = \ q z _ {t+1,x-1} +pz _ {t + 1, x + 1 } ,\ x > - a , $$
with the following obvious boundary conditions:
$$ z _ {t,-a} = 1 ,\ \ 0 \leq t \leq n , $$
$$ z _ {n,x} = 0 ,\ x > -a . $$
The solution of this problem for $ p = q = 1/2 $ was known to A. de Moivre and to P. Laplace. The Laplace formula is:
$$ \tag{* } z _ {t,x} = 1 - \frac{2} \pi \int\limits _ { 0 } ^ { \pi /2 } \frac{\sin (a+x) \phi }{\sin \phi } ( \cos \phi ) ^ \nu d \phi , $$
where
$$ \nu = a + x + 2 \left [ \frac{n-t-x-a}{2} \right ] + 1 . $$
The transition to diffusion processes. As an example, let $ p = q = 1/2 $, $ \Delta t = 1/N $, $ h = 1/ \sqrt N $. Then, as $ N \rightarrow \infty $, many probabilities, calculated for a Bernoulli random walk, tend to limits which are equal to the respective probabilities of a Brownian motion. As an example, consider the probability of a particle, which has departed from zero, reaching a barrier located at a point $ \alpha $ before or at the moment $ T $. The limit transition from formula (*), for $ n/N = T $, $ t = 0 $, $ a/ \sqrt N = \alpha $, gives the magnitude
$$ 1 - \frac{2}{\sqrt {2 \pi } } \int\limits _ { 0 } ^ { \alpha / \sqrt T } e ^ {-z ^ {2} /2 } dz = \ \frac{2}{\sqrt {2 \pi } } \int\limits _ {\alpha / \sqrt T } ^ \infty e ^ {-z ^ {2} /2 } dz , $$
which is equal to the probability that the coordinate $ X( \nu ) $ of a particle executing a Brownian motion satisfies the inequality
$$ \mathop{\rm min} _ {0 \leq \nu \leq T } \ X( \nu ) \leq - \alpha , $$
i.e. to the probability that the particle is absorbed at the barrier $ - \alpha $. For the sake of a more or less complete description of such limit relationships it is expedient to adopt a general standpoint and to consider the transition from the discrete process of "cumulative sums" to a continuous random process (cf. Limit theorems).
The scheme of a Bernoulli random walk is very useful in explaining the characteristic features of the behaviour of sums of random variables such as the strong law of large numbers and the law of the iterated logarithm.
References
| [1] | W. Feller, "An introduction to probability theory and its applications", 1, Wiley (1957) pp. Chapt.14 |
Bernoulli random walk. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bernoulli_random_walk&oldid=46020