Difference between revisions of "Bergman kernel function"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | b0155601.png | ||
| + | $#A+1 = 107 n = 1 | ||
| + | $#C+1 = 107 : ~/encyclopedia/old_files/data/B015/B.0105560 Bergman kernel function, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''Bergman kernel'' | ''Bergman kernel'' | ||
| − | A function of complex variables with the reproducing kernel property, defined for any domain | + | A function of complex variables with the reproducing kernel property, defined for any domain $ D \subset \mathbf C ^ {n} $ |
| + | in which there exist holomorphic functions $ f \neq 0 $ | ||
| + | of class $ L _ {2} (D) $ | ||
| + | with respect to the Lebesgue measure $ dV $. | ||
| + | The function was introduced by S. Bergman [[#References|[1]]]. The set of these functions $ f $ | ||
| + | forms the Hilbert space $ L _ {2,h} (D) \subset L _ {2} (D) $ | ||
| + | with orthonormal basis $ \{ \phi _ {1} , \phi _ {2} ,\dots \} $; | ||
| + | $ L _ {2,h} (D) = L _ {2} (D) \cap O(D) $, | ||
| + | where $ O(D) $ | ||
| + | is the space of holomorphic functions. The function | ||
| − | + | $$ | |
| + | K _ {D} (z, \zeta ) = \ | ||
| + | K (z, \zeta ) = \ | ||
| + | \sum _ { j=1 } ^ \infty | ||
| + | \phi _ {j} (z) | ||
| + | \overline{ {\phi _ {j} ( \zeta ) }}\; , | ||
| + | $$ | ||
| − | + | $$ | |
| + | z = (z _ {1} \dots z _ {n} ),\ \zeta = ( \zeta _ {1} \dots \zeta _ {n} ), | ||
| + | $$ | ||
| − | is called the Bergman kernel function (or simply the kernel function) of | + | is called the Bergman kernel function (or simply the kernel function) of $ D $. |
| + | The series on the right-hand side converges uniformly on compact subsets of $ D $, | ||
| + | and belongs to $ L _ {2,h} (D) $ | ||
| + | for each given $ \zeta \in D $, | ||
| + | the sum does not depend on the choice of the orthonormal basis $ \{ \phi _ {j} \} $. | ||
| + | The Bergman kernel function depends on $ 2n $ | ||
| + | complex variables, and is defined in the domain $ D \times D \subset \mathbf C ^ {2n } $; | ||
| + | it has the symmetry property $ K ( \zeta , z ) = {K(z, \zeta ) } bar $, | ||
| + | it is holomorphic with respect to the variable $ z $ | ||
| + | and anti-holomorphic with respect to $ \zeta $. | ||
| + | If $ D = D ^ \prime \times D ^ {\prime\prime} $, | ||
| + | $ D ^ \prime \subset \mathbf C ^ {m} $, | ||
| + | $ D ^ {\prime\prime} \subset \mathbf C ^ {n - m } $, | ||
| + | then | ||
| − | + | $$ | |
| + | K _ {D} (z, \zeta ) = \ | ||
| + | K _ {D ^ \prime } | ||
| + | (z ^ \prime , \zeta ^ \prime ) | ||
| + | K _ {D ^ {\prime\prime} } | ||
| + | (z ^ {\prime\prime} , \zeta ^ \prime ), | ||
| + | $$ | ||
| − | where | + | where $ z ^ \prime = ( z _ {1} \dots z _ {m} ), z ^ {\prime\prime } = ( z _ {m+1 } \dots z _ {n} ) $. |
| − | The most important characteristic of the Bergman kernel function is its reproducing property: For any function | + | The most important characteristic of the Bergman kernel function is its reproducing property: For any function $ f \in L _ {2,h} (D) $ |
| + | and for any point $ z \in D $ | ||
| + | the following integral representation is valid: | ||
| − | + | $$ | |
| + | f(z) = \int\limits _ { D } f ( \zeta ) K (z, \zeta ) dV ( \zeta ). | ||
| + | $$ | ||
Extremal properties of the Bergman kernel function are: | Extremal properties of the Bergman kernel function are: | ||
| − | 1) For any point | + | 1) For any point $ z \in D $ |
| + | |||
| + | $$ | ||
| + | K (z, z) = \sup \ | ||
| + | \{ {| f (z) | ^ {2} } : { | ||
| + | f \in L _ {2,h} (D),\ | ||
| + | \| f \| _ {L _ {2} (D) } | ||
| + | \leq 1 } \} | ||
| + | . | ||
| + | $$ | ||
| − | + | 2) Let a point $ \zeta \in D $ | |
| + | be such that the class $ L _ {2,h} (D) $ | ||
| + | contains functions satisfying the condition $ f ( \zeta ) = 1 $. | ||
| + | The function $ K(z, \zeta )/K( \zeta , \zeta ) $ | ||
| + | then satisfies this condition and has norm $ K( \zeta , \zeta ) ^ {-1/2} $, | ||
| + | which is minimal for all such $ f $. | ||
| + | The function $ K(z, \zeta )/K( \zeta , \zeta ) $ | ||
| + | is called the extremal function of $ D $. | ||
| − | + | Changes in the Bergman kernel function under biholomorphic mappings are expressed in the following theorem: If $ \phi $ | |
| + | is a biholomorphic mapping of a domain $ D $ | ||
| + | onto a domain $ D ^ {*} $, | ||
| + | $ \phi (z) = w $, | ||
| + | $ \phi ( \zeta ) = \eta $, | ||
| + | then | ||
| − | + | $$ | |
| + | K _ {D ^ {*} } | ||
| + | ( w , \eta ) = \ | ||
| + | K _ {D} (z, \zeta ) \ | ||
| − | + | \frac{dz}{d w } | |
| + | \ | ||
| − | + | \frac{\overline{ {d \zeta }}\; }{d \eta } | |
| + | , | ||
| + | $$ | ||
| − | + | where $ dz / dw $ | |
| + | is the Jacobian of the inverse mapping. Owing to this property the Hermitian quadratic form | ||
| + | |||
| + | $$ | ||
| + | ds ^ {2} = \ | ||
| + | \sum _ { j,k=1 } ^ { n } | ||
| + | |||
| + | \frac{\partial ^ {2} \mathop{\rm log} K(z, z) }{\partial z _ {j} \partial \overline{z}\; _ {k} } | ||
| + | \ | ||
| + | dz _ {j} d \overline{z}\; _ {k} $$ | ||
is invariant under biholomorphic mappings. | is invariant under biholomorphic mappings. | ||
| − | The function | + | The function $ K(z) = K(z, z) $, |
| + | which is also called a kernel function, plays an important role in the intrinsic geometry of domains. In the general case it is non-negative, while the function $ \mathop{\rm log} K (z) $ | ||
| + | is plurisubharmonic. In domains $ D $ | ||
| + | where $ K(z) $ | ||
| + | is positive (e.g. in bounded domains), the functions $ K(z) $ | ||
| + | and $ \mathop{\rm log} K(z) $ | ||
| + | are strictly plurisubharmonic. The latter is tantamount to saying that in such domains $ D $ | ||
| + | the form $ ds ^ {2} $ | ||
| + | is positive definite and, consequently, gives a Hermitian Riemannian metric in $ D $. | ||
| + | This metric remains unchanged under biholomorphic mappings and is called the Bergman metric. It may be considered as a special case of a [[Kähler metric|Kähler metric]]. It follows from extremal property 1) that the coefficients of the Bergman metric increase to infinity on approaching certain boundary points. If $ D \subset \mathbf C ^ {n} $ | ||
| + | is a strictly pseudo-convex domain or an analytic polyhedron, then $ K(z) $ | ||
| + | increases to infinity for any approach of $ z $ | ||
| + | to the boundary of the domain. Every domain which has this property of the Bergman kernel function is a domain of holomorphy. | ||
| − | For domains of the simplest type, the Bergman kernel function can be explicitly calculated. Thus, for the ball | + | For domains of the simplest type, the Bergman kernel function can be explicitly calculated. Thus, for the ball $ B = \{ {z } : {| z | < R } \} $ |
| + | in $ \mathbf C ^ {n} $, | ||
| + | the Bergman function has the following form: | ||
| − | + | $$ | |
| + | K _ {B} (z , \zeta ) = \ | ||
| − | + | \frac{n ! R ^ {n} }{\pi ^ {n} } | |
| − | + | \left ( R ^ {2} - \sum _ { j=1 } ^ { n } | |
| + | z _ {j} \overline \zeta \; _ {j} \right ) ^ {-n-1} , | ||
| + | $$ | ||
| − | + | and for the polydisc $ U = \{ {z } : {| z _ {j} | < R _ {j} , j = 1 \dots n } \} $, | |
| + | in $ \mathbf C ^ {n} $: | ||
| − | + | $$ | |
| + | K _ {U} (z, \zeta ) = \ | ||
| − | which is invariant under conformal mappings and which defines the Lobachevskii geometry in | + | \frac{1}{\pi ^ {n} } |
| + | |||
| + | \prod _ { j=1 } ^ { n } | ||
| + | |||
| + | \frac{R _ {j} ^ {2} }{(R _ {j} ^ {2} -z _ {j} \overline \zeta \; _ {j} ) ^ {2} } | ||
| + | . | ||
| + | $$ | ||
| + | |||
| + | In the special case when $ n=1 $ | ||
| + | and $ U = B $ | ||
| + | is the disc $ \{ {z } : {| z | < R } \} $ | ||
| + | in the complex $ z $- | ||
| + | plane, the Bergman metric becomes the classical hyperbolic metric | ||
| + | |||
| + | $$ | ||
| + | ds ^ {2} = \ | ||
| + | |||
| + | \frac{2R ^ {2} }{(R ^ {2} - | z | ^ {2} ) ^ {2} } | ||
| + | \ | ||
| + | | dz | ^ {2} , | ||
| + | $$ | ||
| + | |||
| + | which is invariant under conformal mappings and which defines the Lobachevskii geometry in $ U $. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> S. Bergman, "The kernel function and conformal mapping" , Amer. Math. Soc. (1950)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B.A. Fuks, "Special chapters in the theory of analytic functions of several complex variables" , Amer. Math. Soc. (1965) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> B.V. Shabat, "Introduction of complex analysis" , '''1–2''' , Moscow (1976) (In Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S. Bergman, "The kernel function and conformal mapping" , Amer. Math. Soc. (1950)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B.A. Fuks, "Special chapters in the theory of analytic functions of several complex variables" , Amer. Math. Soc. (1965) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> B.V. Shabat, "Introduction of complex analysis" , '''1–2''' , Moscow (1976) (In Russian)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | Recently, additional properties of the Bergman kernel have been discovered. For a large class of pseudo-convex domains with | + | Recently, additional properties of the Bergman kernel have been discovered. For a large class of pseudo-convex domains with $ C ^ \infty $ |
| + | boundary, which includes strictly pseudo-convex domains, and domains of finite type, the kernel function $ K (z, w) $ | ||
| + | on $ D \times D $ | ||
| + | is smooth up to the boundary in $ z $ | ||
| + | if $ w $ | ||
| + | remains fixed in $ D $. | ||
| + | This is a consequence of the compactness of the Neumann operator $ N $ | ||
| + | for the complex Laplacian on $ D $ | ||
| + | and the identity | ||
| − | + | $$ | |
| + | P = I - \overline \partial \; * N \overline \partial \; . | ||
| + | $$ | ||
| − | Here | + | Here $ P $ |
| + | is the Bergman projection, that is, the orthogonal projection of $ L _ {2} (D) $ | ||
| + | onto $ L _ {2,h} (D) $ | ||
| + | given by integration against $ K $; | ||
| + | $ \overline \partial \; $ | ||
| + | is the Cauchy–Riemann operator and $ \overline \partial \; ^ {*} $ | ||
| + | its Hilbert space adjoint. In fact, for these domains $ P $ | ||
| + | satisfies the so-called "condition R for the Bergman projectioncondition R" , that is $ P $ | ||
| + | maps $ L _ {2, s + 2 } (D) $ | ||
| + | continuously into $ L _ {2,s} (D) $, | ||
| + | where $ L _ {2,k} (D) $ | ||
| + | denotes the [[Sobolev space|Sobolev space]] of order $ k $. | ||
| + | This property of the Bergman kernel function is employed in the study of proper holomorphic and biholomorphic mappings. (See [[#References|[a2]]], [[#References|[a4]]], [[#References|[a5]]].) Moreover, the asymptotic behaviour of $ K (z, w) $ | ||
| + | has been studied; for strictly pseudo-convex domains $ D $ | ||
| + | one has | ||
| − | + | $$ | |
| + | K (z, w) = \ | ||
| + | F (z, w) | ||
| + | (i \psi (z, w)) ^ {- n - 1 } + | ||
| + | G (z, w) \mathop{\rm log} \ | ||
| + | (i \psi (z, w)), | ||
| + | $$ | ||
| − | where | + | where $ F, G $ |
| + | and $ \psi $ | ||
| + | are $ C ^ \infty $ | ||
| + | functions on $ \overline{D}\; \times \overline{D}\; $ | ||
| + | and $ \psi $ | ||
| + | satisfies | ||
| − | a) | + | a) $ \psi (z, z) = \rho (z)/i $, |
| + | where $ \rho $ | ||
| + | is a strictly-plurisubharmonic defining function for $ D $; | ||
| − | b) | + | b) $ \overline \partial \; _ {z} \psi $ |
| + | and $ \overline \partial \; _ {w} \psi $ | ||
| + | vanish to infinite order at $ z = w $; | ||
| + | and | ||
| − | c) | + | c) $ \psi (z, w) = {- \psi (w, z) } bar $. |
Similar results have been obtained for certain weakly pseudo-convex domains, see [[#References|[a1]]], [[#References|[a3]]], [[#References|[a4]]]. | Similar results have been obtained for certain weakly pseudo-convex domains, see [[#References|[a1]]], [[#References|[a3]]], [[#References|[a4]]]. | ||
Revision as of 10:58, 29 May 2020
Bergman kernel
A function of complex variables with the reproducing kernel property, defined for any domain $ D \subset \mathbf C ^ {n} $ in which there exist holomorphic functions $ f \neq 0 $ of class $ L _ {2} (D) $ with respect to the Lebesgue measure $ dV $. The function was introduced by S. Bergman [1]. The set of these functions $ f $ forms the Hilbert space $ L _ {2,h} (D) \subset L _ {2} (D) $ with orthonormal basis $ \{ \phi _ {1} , \phi _ {2} ,\dots \} $; $ L _ {2,h} (D) = L _ {2} (D) \cap O(D) $, where $ O(D) $ is the space of holomorphic functions. The function
$$ K _ {D} (z, \zeta ) = \ K (z, \zeta ) = \ \sum _ { j=1 } ^ \infty \phi _ {j} (z) \overline{ {\phi _ {j} ( \zeta ) }}\; , $$
$$ z = (z _ {1} \dots z _ {n} ),\ \zeta = ( \zeta _ {1} \dots \zeta _ {n} ), $$
is called the Bergman kernel function (or simply the kernel function) of $ D $. The series on the right-hand side converges uniformly on compact subsets of $ D $, and belongs to $ L _ {2,h} (D) $ for each given $ \zeta \in D $, the sum does not depend on the choice of the orthonormal basis $ \{ \phi _ {j} \} $. The Bergman kernel function depends on $ 2n $ complex variables, and is defined in the domain $ D \times D \subset \mathbf C ^ {2n } $; it has the symmetry property $ K ( \zeta , z ) = {K(z, \zeta ) } bar $, it is holomorphic with respect to the variable $ z $ and anti-holomorphic with respect to $ \zeta $. If $ D = D ^ \prime \times D ^ {\prime\prime} $, $ D ^ \prime \subset \mathbf C ^ {m} $, $ D ^ {\prime\prime} \subset \mathbf C ^ {n - m } $, then
$$ K _ {D} (z, \zeta ) = \ K _ {D ^ \prime } (z ^ \prime , \zeta ^ \prime ) K _ {D ^ {\prime\prime} } (z ^ {\prime\prime} , \zeta ^ \prime ), $$
where $ z ^ \prime = ( z _ {1} \dots z _ {m} ), z ^ {\prime\prime } = ( z _ {m+1 } \dots z _ {n} ) $.
The most important characteristic of the Bergman kernel function is its reproducing property: For any function $ f \in L _ {2,h} (D) $ and for any point $ z \in D $ the following integral representation is valid:
$$ f(z) = \int\limits _ { D } f ( \zeta ) K (z, \zeta ) dV ( \zeta ). $$
Extremal properties of the Bergman kernel function are:
1) For any point $ z \in D $
$$ K (z, z) = \sup \ \{ {| f (z) | ^ {2} } : { f \in L _ {2,h} (D),\ \| f \| _ {L _ {2} (D) } \leq 1 } \} . $$
2) Let a point $ \zeta \in D $ be such that the class $ L _ {2,h} (D) $ contains functions satisfying the condition $ f ( \zeta ) = 1 $. The function $ K(z, \zeta )/K( \zeta , \zeta ) $ then satisfies this condition and has norm $ K( \zeta , \zeta ) ^ {-1/2} $, which is minimal for all such $ f $. The function $ K(z, \zeta )/K( \zeta , \zeta ) $ is called the extremal function of $ D $.
Changes in the Bergman kernel function under biholomorphic mappings are expressed in the following theorem: If $ \phi $ is a biholomorphic mapping of a domain $ D $ onto a domain $ D ^ {*} $, $ \phi (z) = w $, $ \phi ( \zeta ) = \eta $, then
$$ K _ {D ^ {*} } ( w , \eta ) = \ K _ {D} (z, \zeta ) \ \frac{dz}{d w } \ \frac{\overline{ {d \zeta }}\; }{d \eta } , $$
where $ dz / dw $ is the Jacobian of the inverse mapping. Owing to this property the Hermitian quadratic form
$$ ds ^ {2} = \ \sum _ { j,k=1 } ^ { n } \frac{\partial ^ {2} \mathop{\rm log} K(z, z) }{\partial z _ {j} \partial \overline{z}\; _ {k} } \ dz _ {j} d \overline{z}\; _ {k} $$
is invariant under biholomorphic mappings.
The function $ K(z) = K(z, z) $, which is also called a kernel function, plays an important role in the intrinsic geometry of domains. In the general case it is non-negative, while the function $ \mathop{\rm log} K (z) $ is plurisubharmonic. In domains $ D $ where $ K(z) $ is positive (e.g. in bounded domains), the functions $ K(z) $ and $ \mathop{\rm log} K(z) $ are strictly plurisubharmonic. The latter is tantamount to saying that in such domains $ D $ the form $ ds ^ {2} $ is positive definite and, consequently, gives a Hermitian Riemannian metric in $ D $. This metric remains unchanged under biholomorphic mappings and is called the Bergman metric. It may be considered as a special case of a Kähler metric. It follows from extremal property 1) that the coefficients of the Bergman metric increase to infinity on approaching certain boundary points. If $ D \subset \mathbf C ^ {n} $ is a strictly pseudo-convex domain or an analytic polyhedron, then $ K(z) $ increases to infinity for any approach of $ z $ to the boundary of the domain. Every domain which has this property of the Bergman kernel function is a domain of holomorphy.
For domains of the simplest type, the Bergman kernel function can be explicitly calculated. Thus, for the ball $ B = \{ {z } : {| z | < R } \} $ in $ \mathbf C ^ {n} $, the Bergman function has the following form:
$$ K _ {B} (z , \zeta ) = \ \frac{n ! R ^ {n} }{\pi ^ {n} } \left ( R ^ {2} - \sum _ { j=1 } ^ { n } z _ {j} \overline \zeta \; _ {j} \right ) ^ {-n-1} , $$
and for the polydisc $ U = \{ {z } : {| z _ {j} | < R _ {j} , j = 1 \dots n } \} $, in $ \mathbf C ^ {n} $:
$$ K _ {U} (z, \zeta ) = \ \frac{1}{\pi ^ {n} } \prod _ { j=1 } ^ { n } \frac{R _ {j} ^ {2} }{(R _ {j} ^ {2} -z _ {j} \overline \zeta \; _ {j} ) ^ {2} } . $$
In the special case when $ n=1 $ and $ U = B $ is the disc $ \{ {z } : {| z | < R } \} $ in the complex $ z $- plane, the Bergman metric becomes the classical hyperbolic metric
$$ ds ^ {2} = \ \frac{2R ^ {2} }{(R ^ {2} - | z | ^ {2} ) ^ {2} } \ | dz | ^ {2} , $$
which is invariant under conformal mappings and which defines the Lobachevskii geometry in $ U $.
References
| [1] | S. Bergman, "The kernel function and conformal mapping" , Amer. Math. Soc. (1950) |
| [2] | B.A. Fuks, "Special chapters in the theory of analytic functions of several complex variables" , Amer. Math. Soc. (1965) (Translated from Russian) |
| [3] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) |
Comments
Recently, additional properties of the Bergman kernel have been discovered. For a large class of pseudo-convex domains with $ C ^ \infty $ boundary, which includes strictly pseudo-convex domains, and domains of finite type, the kernel function $ K (z, w) $ on $ D \times D $ is smooth up to the boundary in $ z $ if $ w $ remains fixed in $ D $. This is a consequence of the compactness of the Neumann operator $ N $ for the complex Laplacian on $ D $ and the identity
$$ P = I - \overline \partial \; * N \overline \partial \; . $$
Here $ P $ is the Bergman projection, that is, the orthogonal projection of $ L _ {2} (D) $ onto $ L _ {2,h} (D) $ given by integration against $ K $; $ \overline \partial \; $ is the Cauchy–Riemann operator and $ \overline \partial \; ^ {*} $ its Hilbert space adjoint. In fact, for these domains $ P $ satisfies the so-called "condition R for the Bergman projectioncondition R" , that is $ P $ maps $ L _ {2, s + 2 } (D) $ continuously into $ L _ {2,s} (D) $, where $ L _ {2,k} (D) $ denotes the Sobolev space of order $ k $. This property of the Bergman kernel function is employed in the study of proper holomorphic and biholomorphic mappings. (See [a2], [a4], [a5].) Moreover, the asymptotic behaviour of $ K (z, w) $ has been studied; for strictly pseudo-convex domains $ D $ one has
$$ K (z, w) = \ F (z, w) (i \psi (z, w)) ^ {- n - 1 } + G (z, w) \mathop{\rm log} \ (i \psi (z, w)), $$
where $ F, G $ and $ \psi $ are $ C ^ \infty $ functions on $ \overline{D}\; \times \overline{D}\; $ and $ \psi $ satisfies
a) $ \psi (z, z) = \rho (z)/i $, where $ \rho $ is a strictly-plurisubharmonic defining function for $ D $;
b) $ \overline \partial \; _ {z} \psi $ and $ \overline \partial \; _ {w} \psi $ vanish to infinite order at $ z = w $; and
c) $ \psi (z, w) = {- \psi (w, z) } bar $.
Similar results have been obtained for certain weakly pseudo-convex domains, see [a1], [a3], [a4].
The Bergman kernel has also been studied for other domains, e.g. Cartan domains (cf. [a6]) and Siegel domains (cf. [a7], Siegel domain).
References
| [a1] | L. Boutet de Monvel, J. Sjöstrand, "Sur la singularité des noyaux de Bergman et de Szegö" Astérisque , 34–35 (1976) pp. 123–164 |
| [a2] | D. Catlin, "Global regularity of the 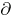 -Neumann problem" , Proc. Symp. Pure Math. , 41 , Amer. Math. Soc. (1984) pp. 39–49 -Neumann problem" , Proc. Symp. Pure Math. , 41 , Amer. Math. Soc. (1984) pp. 39–49 |
| [a3] | K. Diederich, G. Herbort, T. Ohsawa, "The Bergman kernel on uniformly extendable pseudo-convex domains" Math. Ann. , 273 (1986) pp. 471–478 |
| [a4] | C. Fefferman, "The Bergman kernel and biholomorphic mappings of pseudo-convex domains" Invent. Math. , 37 (1974) pp. 1–65 |
| [a5] | R.M. Range, "Holomorphic functions and integral representation in several complex variables" , Springer (1986) pp. Chapt. 7 |
| [a6] | L.K. Hua, "Harmonic analysis of functions of several complex variables in the classical domains" , Amer. Math. Soc. (1963) |
| [a7] | S.G. Gindikin, "Analysis on homogeneous domains" Russian Math. Surveys , 19 (1964) pp. 1–89 Uspekhi Mat. Nauk , 19 (1964) pp. 3–92 |
Bergman kernel function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bergman_kernel_function&oldid=46016