Difference between revisions of "Baskakov operators"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | b1101501.png | ||
| + | $#A+1 = 28 n = 1 | ||
| + | $#C+1 = 28 : ~/encyclopedia/old_files/data/B110/B.1100150 Baskakov operators | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| + | |||
| + | V.A. Baskakov [[#References|[a2]]] introduced a sequence of linear positive operators $ L _ {n} $ | ||
| + | with weights | ||
| + | |||
| + | $$ | ||
| + | p _ {nk } ( x ) = ( - 1 ) ^ {k} { | ||
| + | \frac{x ^ {k} }{k! } | ||
| + | } \phi _ {n} ^ {( k ) } ( x ) | ||
| + | $$ | ||
by | by | ||
| − | + | $$ \tag{a1 } | |
| + | ( L _ {n} f ) ( x ) = \sum _ {k = 0 } ^ \infty p _ {nk } ( x ) f \left ( { | ||
| + | \frac{k}{n} | ||
| + | } \right ) , | ||
| + | $$ | ||
| − | where | + | where $ n \in \mathbf N $, |
| + | $ x \in [ 0,b ] $, | ||
| + | $ b > 0 $, | ||
| + | for all functions $ f $ | ||
| + | on $ [ 0, \infty ) $ | ||
| + | for which the series converges. Here, $ \{ \phi _ {n} \} _ {n \in \mathbf N } $ | ||
| + | is a sequence of functions defined on $ [0,b] $ | ||
| + | having the following properties for every $ n,k \in \mathbf N $, | ||
| + | $ k > 0 $: | ||
| − | i) | + | i) $ \phi _ {n} \in C ^ \infty [ 0,b ] $; |
| − | ii) | + | ii) $ \phi _ {n} ( 0 ) = 1 $; |
| − | iii) | + | iii) $ \phi _ {n} $ |
| + | is completely monotone, i.e., $ ( - 1 ) ^ {k} \phi _ {n} ^ {( k ) } \geq 0 $; | ||
| − | iv) there exists an integer | + | iv) there exists an integer $ c $ |
| + | such that $ \phi _ {n} ^ {( k+1 ) } = - n \phi _ {n + c } ^ {( k ) } $, | ||
| + | $ n > \max \{ 0, - c \} $. | ||
Baskakov studied convergence theorems of bounded continuous functions for the operators (a1). For saturation classes for continuous functions with compact support, see [[#References|[a8]]]. For a result concerning bounded continuous functions, see [[#References|[a3]]]. | Baskakov studied convergence theorems of bounded continuous functions for the operators (a1). For saturation classes for continuous functions with compact support, see [[#References|[a8]]]. For a result concerning bounded continuous functions, see [[#References|[a3]]]. | ||
| − | In his work on Baskakov operators, C.P. May [[#References|[a6]]] took conditions slightly different from those mentioned above and showed that the local inverse and saturation theorems hold for functions with growth less than | + | In his work on Baskakov operators, C.P. May [[#References|[a6]]] took conditions slightly different from those mentioned above and showed that the local inverse and saturation theorems hold for functions with growth less than $ ( 1 + t ) ^ {N} $ |
| + | for some $ N > 0 $. | ||
| + | Bernstein polynomials and Szász–Mirakian operators are the particular cases of Baskakov operators considered by May. | ||
S.P. Singh [[#References|[a7]]] studied simultaneous approximation, using another modification of the conditions in the original definition of Baskakov operators. However, it was shown that his result is not correct (cf., e.g., [[#References|[a1]]], Remarks). | S.P. Singh [[#References|[a7]]] studied simultaneous approximation, using another modification of the conditions in the original definition of Baskakov operators. However, it was shown that his result is not correct (cf., e.g., [[#References|[a1]]], Remarks). | ||
| − | Motivated by the Durrmeyer integral modification of the Bernstein polynomials, M. Heilmann [[#References|[a4]]] modified the Baskakov operators in a similar manner by replacing the discrete values | + | Motivated by the Durrmeyer integral modification of the Bernstein polynomials, M. Heilmann [[#References|[a4]]] modified the Baskakov operators in a similar manner by replacing the discrete values $ f ( {k / n } ) $ |
| + | in (a1) by an integral over the weighted function, namely, | ||
| − | + | $$ | |
| + | ( M _ {n} f ) ( x ) = \sum _ {k = 0 } ^ \infty p _ {nk } ( x ) ( n - c ) \int\limits _ { 0 } ^ \infty {p _ {nk } ( t ) f ( t ) } {dt } , | ||
| + | $$ | ||
| − | + | $$ | |
| + | n > c, x \in [ 0, \infty ) , | ||
| + | $$ | ||
| − | where | + | where $ f $ |
| + | is a function on $ [ 0, \infty ) $ | ||
| + | for which the right-hand side is defined. He studied global direct and inverse $ L _ {p} $- | ||
| + | approximation theorems for these operators. | ||
| − | Subsequently, a global direct result for simultaneous approximation in the | + | Subsequently, a global direct result for simultaneous approximation in the $ L _ {p} $- |
| + | metric in terms of the second-order Ditzian–Totik modulus of smoothness was proved, see [[#References|[a5]]]. For local direct results for simultaneous approximation of functions with polynomial growth, see [[#References|[a5]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.N. Agrawal, H.S. Kasana, "On simultaneous approximation by Szász–Mirakian operators" ''Bull. Inst. Math. Acad. Sinica'' , '''22''' (1994) pp. 181–188</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> V.A. Baskakov, "An example of a sequence of linear positive operators in the space of continuous functions" ''Dokl. Akad. Nauk SSSR'' , '''113''' (1957) pp. 249–251 (In Russian)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H. Berens, "Pointwise saturation of positive operators" ''J. Approx. Th.'' , '''6''' (1972) pp. 135–146</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Heilmann, "Approximation auf <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110150/b11015029.png" /> durch das Verfahren der Operatoren vom Baskakov–Durrmeyer Typ" , Univ. Dortmund (1987) (Dissertation)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> M. Heilmann, M.W. Müller, "On simultaneous approximation by the method of Baskakov–Durrmeyer operators" ''Numer. Funct. Anal. Optim.'' , '''10''' (1989) pp. 127–138</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> C.P. May, "Saturation and inverse theorems for combinations of a class of exponential-type operators" ''Canad. J. Math.'' , '''28''' (1976) pp. 1224–1250</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> S.P. Singh, "On Baskakov-type operators" ''Comment. Math. Univ. St. Pauli,'' , '''31''' (1982) pp. 137–142</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> Y. Suzuki, "Saturation of local approximation by linear positive operators of Bernstein type" ''Tôhoku Math. J.'' , '''19''' (1967) pp. 429–453</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.N. Agrawal, H.S. Kasana, "On simultaneous approximation by Szász–Mirakian operators" ''Bull. Inst. Math. Acad. Sinica'' , '''22''' (1994) pp. 181–188</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> V.A. Baskakov, "An example of a sequence of linear positive operators in the space of continuous functions" ''Dokl. Akad. Nauk SSSR'' , '''113''' (1957) pp. 249–251 (In Russian)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H. Berens, "Pointwise saturation of positive operators" ''J. Approx. Th.'' , '''6''' (1972) pp. 135–146</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M. Heilmann, "Approximation auf <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110150/b11015029.png" /> durch das Verfahren der Operatoren vom Baskakov–Durrmeyer Typ" , Univ. Dortmund (1987) (Dissertation)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> M. Heilmann, M.W. Müller, "On simultaneous approximation by the method of Baskakov–Durrmeyer operators" ''Numer. Funct. Anal. Optim.'' , '''10''' (1989) pp. 127–138</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> C.P. May, "Saturation and inverse theorems for combinations of a class of exponential-type operators" ''Canad. J. Math.'' , '''28''' (1976) pp. 1224–1250</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> S.P. Singh, "On Baskakov-type operators" ''Comment. Math. Univ. St. Pauli,'' , '''31''' (1982) pp. 137–142</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> Y. Suzuki, "Saturation of local approximation by linear positive operators of Bernstein type" ''Tôhoku Math. J.'' , '''19''' (1967) pp. 429–453</TD></TR></table> | ||
Revision as of 10:13, 29 May 2020
V.A. Baskakov [a2] introduced a sequence of linear positive operators $ L _ {n} $
with weights
$$ p _ {nk } ( x ) = ( - 1 ) ^ {k} { \frac{x ^ {k} }{k! } } \phi _ {n} ^ {( k ) } ( x ) $$
by
$$ \tag{a1 } ( L _ {n} f ) ( x ) = \sum _ {k = 0 } ^ \infty p _ {nk } ( x ) f \left ( { \frac{k}{n} } \right ) , $$
where $ n \in \mathbf N $, $ x \in [ 0,b ] $, $ b > 0 $, for all functions $ f $ on $ [ 0, \infty ) $ for which the series converges. Here, $ \{ \phi _ {n} \} _ {n \in \mathbf N } $ is a sequence of functions defined on $ [0,b] $ having the following properties for every $ n,k \in \mathbf N $, $ k > 0 $:
i) $ \phi _ {n} \in C ^ \infty [ 0,b ] $;
ii) $ \phi _ {n} ( 0 ) = 1 $;
iii) $ \phi _ {n} $ is completely monotone, i.e., $ ( - 1 ) ^ {k} \phi _ {n} ^ {( k ) } \geq 0 $;
iv) there exists an integer $ c $ such that $ \phi _ {n} ^ {( k+1 ) } = - n \phi _ {n + c } ^ {( k ) } $, $ n > \max \{ 0, - c \} $.
Baskakov studied convergence theorems of bounded continuous functions for the operators (a1). For saturation classes for continuous functions with compact support, see [a8]. For a result concerning bounded continuous functions, see [a3].
In his work on Baskakov operators, C.P. May [a6] took conditions slightly different from those mentioned above and showed that the local inverse and saturation theorems hold for functions with growth less than $ ( 1 + t ) ^ {N} $ for some $ N > 0 $. Bernstein polynomials and Szász–Mirakian operators are the particular cases of Baskakov operators considered by May.
S.P. Singh [a7] studied simultaneous approximation, using another modification of the conditions in the original definition of Baskakov operators. However, it was shown that his result is not correct (cf., e.g., [a1], Remarks).
Motivated by the Durrmeyer integral modification of the Bernstein polynomials, M. Heilmann [a4] modified the Baskakov operators in a similar manner by replacing the discrete values $ f ( {k / n } ) $ in (a1) by an integral over the weighted function, namely,
$$ ( M _ {n} f ) ( x ) = \sum _ {k = 0 } ^ \infty p _ {nk } ( x ) ( n - c ) \int\limits _ { 0 } ^ \infty {p _ {nk } ( t ) f ( t ) } {dt } , $$
$$ n > c, x \in [ 0, \infty ) , $$
where $ f $ is a function on $ [ 0, \infty ) $ for which the right-hand side is defined. He studied global direct and inverse $ L _ {p} $- approximation theorems for these operators.
Subsequently, a global direct result for simultaneous approximation in the $ L _ {p} $- metric in terms of the second-order Ditzian–Totik modulus of smoothness was proved, see [a5]. For local direct results for simultaneous approximation of functions with polynomial growth, see [a5].
References
| [a1] | P.N. Agrawal, H.S. Kasana, "On simultaneous approximation by Szász–Mirakian operators" Bull. Inst. Math. Acad. Sinica , 22 (1994) pp. 181–188 |
| [a2] | V.A. Baskakov, "An example of a sequence of linear positive operators in the space of continuous functions" Dokl. Akad. Nauk SSSR , 113 (1957) pp. 249–251 (In Russian) |
| [a3] | H. Berens, "Pointwise saturation of positive operators" J. Approx. Th. , 6 (1972) pp. 135–146 |
| [a4] | M. Heilmann, "Approximation auf 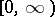 durch das Verfahren der Operatoren vom Baskakov–Durrmeyer Typ" , Univ. Dortmund (1987) (Dissertation) durch das Verfahren der Operatoren vom Baskakov–Durrmeyer Typ" , Univ. Dortmund (1987) (Dissertation) |
| [a5] | M. Heilmann, M.W. Müller, "On simultaneous approximation by the method of Baskakov–Durrmeyer operators" Numer. Funct. Anal. Optim. , 10 (1989) pp. 127–138 |
| [a6] | C.P. May, "Saturation and inverse theorems for combinations of a class of exponential-type operators" Canad. J. Math. , 28 (1976) pp. 1224–1250 |
| [a7] | S.P. Singh, "On Baskakov-type operators" Comment. Math. Univ. St. Pauli, , 31 (1982) pp. 137–142 |
| [a8] | Y. Suzuki, "Saturation of local approximation by linear positive operators of Bernstein type" Tôhoku Math. J. , 19 (1967) pp. 429–453 |
Baskakov operators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Baskakov_operators&oldid=45993