Difference between revisions of "Asymmetry coefficient"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (typos fixed) |
||
| Line 14: | Line 14: | ||
$$ | $$ | ||
| − | \gamma _ {1} = | + | \gamma _ {1} = |
| − | \frac{3}{\mu _ {2} ^ {3/2} } | + | \frac{\mu _ 3}{\mu _ {2} ^ {3/2} } |
, | , | ||
$$ | $$ | ||
| Line 29: | Line 29: | ||
$$ \tag{* } | $$ \tag{* } | ||
| − | \gamma _ {1} = { | + | \gamma _ {1} = |
| − | \sqrt {np ( 1 - p ) } , | + | \frac{1 - 2 p }{\sqrt {np ( 1 - p ) }} |
| + | , | ||
$$ | $$ | ||
| Line 64: | Line 65: | ||
$$ | $$ | ||
| − | \frac{( X _ {1} + \dots + X _ {n} ) - n \mu _ {1} } \sqrt | + | \frac{( X _ {1} + \dots + X _ {n} ) - n \mu _ {1} }{\sqrt {n \mu _ {2} }} |
| − | + | , | |
$$ | $$ | ||
| Line 74: | Line 75: | ||
$$ | $$ | ||
\Phi (x) = | \Phi (x) = | ||
| − | \frac{1} \sqrt | + | \frac{1}{\sqrt {2 \pi }} |
| − | + | \int\limits _ {- \infty } ^ { x } | |
e ^ {-z ^ {2} /2 } dz . | e ^ {-z ^ {2} /2 } dz . | ||
$$ | $$ | ||
| Line 82: | Line 83: | ||
$$ | $$ | ||
| − | F _ {n} (x) = \Phi (x) - | + | F _ {n} (x) = \Phi (x) - |
| − | \frac{1} \sqrt | + | \frac{1}{\sqrt n} |
| − | + | ||
| − | \frac{1}{6} | + | \frac{\gamma _ 1}{6} |
\Phi ^ {(3)} (x) + O \left ( | \Phi ^ {(3)} (x) + O \left ( | ||
Revision as of 17:32, 6 April 2020
The most frequently employed measure of the asymmetry of a distribution, defined by the relationship
$$ \gamma _ {1} = \frac{\mu _ 3}{\mu _ {2} ^ {3/2} } , $$
where $ \mu _ {2} $ and $ \mu _ {3} $ are the second and third central moments of the distribution, respectively. For distributions that are symmetric with respect to the mathematical expectation, $ \gamma _ {1} = 0 $; depending on the sign of $ \gamma _ {1} $ one speaks of positive asymmetry ( $ \gamma _ {1} > 0 $) and negative asymmetry ( $ \gamma _ {1} < 0 $). In the case of the binomial distribution corresponding to $ n $[[ Bernoulli trials|Bernoulli trials]] with probability of success $ p $,
$$ \tag{* } \gamma _ {1} = \frac{1 - 2 p }{\sqrt {np ( 1 - p ) }} , $$
one has: If $ p = 1/2 ( \gamma _ {1} = 0 ) $, the distribution is symmetric; if $ p < 1/2 $ or $ p > 1/2 $, one obtains typical distribution diagrams with a positive (Fig.a) and negative (Fig.b) asymmetry.
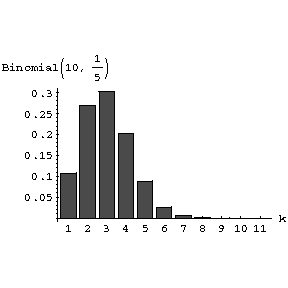
Figure: a013590a
$ P(k, 10, 1/5 ) $. Diagram of the binomial distribution $ P(k, n, p) $ corresponding to $ n = 10 $ Bernoulli trials, with positive asymmetry ( $ p = 1/5 $).

Figure: a013590b
$ P(k, 10, 4/5 ) $. Diagram of the binomial distribution $ P(k, n, p) $ corresponding to $ n = 10 $ Bernoulli trials, with negative asymmetry ( $ p = 4/5 $).
The asymmetry coefficient (*) tends to zero as $ n \rightarrow \infty $, in accordance with the fact that a normalized binomial distribution converges to the standard normal distribution.
The asymmetry coefficient and the excess coefficient are the most extensively used characteristics of the accuracy with which the distribution function $ F _ {n} (x) $ of the normalized sum
$$ \frac{( X _ {1} + \dots + X _ {n} ) - n \mu _ {1} }{\sqrt {n \mu _ {2} }} , $$
where $ X _ {1} \dots X _ {n} $ are identically distributed and mutually independent with asymmetry coefficient $ \delta _ {1} $, may be approximated by the normal distribution function
$$ \Phi (x) = \frac{1}{\sqrt {2 \pi }} \int\limits _ {- \infty } ^ { x } e ^ {-z ^ {2} /2 } dz . $$
Under fairly general conditions the Edgeworth series yields
$$ F _ {n} (x) = \Phi (x) - \frac{1}{\sqrt n} \frac{\gamma _ 1}{6} \Phi ^ {(3)} (x) + O \left ( \frac{1}{n} \right ) , $$
where $ \Phi ^ {(3)} (x) $ is the derivative of order three.
References
| [1] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [2] | S.S. Wilks, "Mathematical statistics" , Wiley (1962) |
Comments
The asymmetry coefficient is usually called the coefficient of skewness. One correspondingly speaks of the skewness of a distribution and of positive, respectively negative, skewness.
The excess coefficient is more often called the coefficient of kurtosis.
Asymmetry coefficient. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Asymmetry_coefficient&oldid=45287