Difference between revisions of "Arens regularity"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | a1106701.png | ||
| + | $#A+1 = 52 n = 2 | ||
| + | $#C+1 = 52 : ~/encyclopedia/old_files/data/A110/A.1100670 Arens regularity | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A [[Normed algebra|normed algebra]] $ A $ | |
| + | is said to be Arens regular if the pair of intrinsically defined Arens products (introduced by R. Arens in [[#References|[a1]]] and [[#References|[a2]]]; cf. [[Arens multiplication|Arens multiplication]]) on the double dual space $ A ^ {* * } $ | ||
| + | are identical. Since both Arens products extend the product on $ A $( | ||
| + | relative to the natural embedding mapping $ \kappa : A \rightarrow {A ^ {* * } } $), | ||
| + | a [[Banach algebra|Banach algebra]] on a reflexive [[Banach space|Banach space]] (cf. also [[Reflexive space|Reflexive space]]) is Arens regular. S. Sherman has shown [[#References|[a10]]] that the double dual of a [[C*-algebra| $ C ^ {*} $- | ||
| + | algebra]] $ A $ | ||
| + | has a natural interpretation as the [[Von Neumann algebra|von Neumann algebra]] generated by the universal $ * $- | ||
| + | representation of $ A $. | ||
| + | Hence $ C ^ {*} $- | ||
| + | algebras are always Arens regular. | ||
| − | + | It is easy to show that if $ A ^ {* * } $ | |
| + | is commutative under either Arens product, then $ A $ | ||
| + | is Arens regular. The following fundamental result is due to J. Hennefeld [[#References|[a5]]], based on work of J.S. Pym [[#References|[a8]]] making use of Grothendieck's criterion for weak compactness. | ||
| − | + | The following conditions are equivalent for a Banach algebra $ A $: | |
| − | + | a) $ A $ | |
| + | is Arens regular; | ||
| − | + | b) for each $ a \in A $ | |
| + | the adjoint $ {L _ {a} ^ {*} } : {A ^ {*} } \rightarrow {A ^ {*} } $ | ||
| + | of the left regular representation is weakly compact; | ||
| − | + | c) for each $ a \in A $ | |
| + | the adjoint $ {R _ {a} ^ {*} } : {A ^ {*} } \rightarrow {A ^ {*} } $ | ||
| + | of the right regular representation is weakly compact; | ||
| + | |||
| + | d) for any bounded sequences $ \{ a _ {n} \} _ {n \in \mathbf N } $ | ||
| + | and $ \{ b _ {n} \} _ {n \in \mathbf N } $ | ||
| + | in $ A $ | ||
| + | and any $ \omega \in A ^ {*} $, | ||
| + | the iterated limits | ||
| + | |||
| + | $$ | ||
| + | {\lim\limits } _ { n } {\lim\limits } _ { m } \omega ( a _ {n} b _ {n} ) , \quad {\lim\limits } _ { m } {\lim\limits } _ { n } \omega ( a _ {n} b _ {n} ) | ||
| + | $$ | ||
are equal when they both exist. | are equal when they both exist. | ||
| Line 19: | Line 53: | ||
This theorem easily implies that subalgebras and quotient algebras (with respect to closed ideals) of Arens-regular algebras are Arens regular, as first noted in [[#References|[a3]]]. | This theorem easily implies that subalgebras and quotient algebras (with respect to closed ideals) of Arens-regular algebras are Arens regular, as first noted in [[#References|[a3]]]. | ||
| − | Arens regularity is rare among general Banach algebras. N.J. Young [[#References|[a11]]] has shown that for a locally compact group (cf. also [[Compact group|Compact group]]; [[Locally compact skew-field|Locally compact skew-field]]) | + | Arens regularity is rare among general Banach algebras. N.J. Young [[#References|[a11]]] has shown that for a locally compact group (cf. also [[Compact group|Compact group]]; [[Locally compact skew-field|Locally compact skew-field]]) $ G $, |
| + | $ L ^ {1} ( G ) $( | ||
| + | or $ M ( G ) $) | ||
| + | is Arens regular if and only if $ G $ | ||
| + | is finite. P. Civin and B. Yood had proved this for Abelian groups in [[#References|[a3]]]. In [[#References|[a12]]] it is shown that the measure algebra (cf. [[Algebra of measures|Algebra of measures]]) $ M ( S ) $ | ||
| + | of a locally compact semi-group $ S $ | ||
| + | in which multiplication is at least singly continuous is Arens regular if and only if $ {\mathcal l} ^ {1} ( S ) $ | ||
| + | is. These are, in turn, equivalent to either: | ||
| − | there do not exist sequences | + | there do not exist sequences $ \{ u _ {n} \} $ |
| + | and $ \{ v _ {m} \} $ | ||
| + | in $ S $ | ||
| + | such that the sets $ \{ {u _ {n} v _ {m} } : {m > n } \} $ | ||
| + | and $ \{ {u _ {n} v _ {m} } : {m < n } \} $ | ||
| + | are disjoint; | ||
| − | the semi-group operation can be extended to the [[Stone–Čech compactification|Stone–Čech compactification]] | + | the semi-group operation can be extended to the [[Stone–Čech compactification|Stone–Čech compactification]] $ \beta S $ |
| + | of $ S $ | ||
| + | as a discrete space. | ||
| − | In [[#References|[a13]]], Young has proved that the algebra | + | In [[#References|[a13]]], Young has proved that the algebra $ B _ {A} ( X ) $ |
| + | of approximable operators (i.e., those uniformly approximable by finite-rank operators) on a Banach space $ X $ | ||
| + | is regular if and only if $ X $ | ||
| + | is reflexive (cf. [[Reflexive space|Reflexive space]]). Hence, if the Banach algebra $ B ( X ) $ | ||
| + | of all bounded linear operators on a Banach space $ X $ | ||
| + | is Arens regular, then $ X $ | ||
| + | must be reflexive. He also shows that there are reflexive Banach spaces $ X $ | ||
| + | with $ B ( X ) $ | ||
| + | not Arens regular. | ||
| − | Á. Rodriguez-Palacios [[#References|[a9]]] has shown that any (even non-associative) continuous multiplication on a Banach space | + | Á. Rodriguez-Palacios [[#References|[a9]]] has shown that any (even non-associative) continuous multiplication on a Banach space $ A $ |
| + | is Arens regular if and only if every bounded linear mapping from $ A $ | ||
| + | into $ A ^ {*} $ | ||
| + | is weakly compact (cf. [[Weak topology|Weak topology]]). $ C ^ {*} $- | ||
| + | algebras satisfy this criterion. | ||
| − | A weaker version of Arens regularity was introduced by M. Grosser [[#References|[a4]]]. An approximately unital [[Banach algebra|Banach algebra]] | + | A weaker version of Arens regularity was introduced by M. Grosser [[#References|[a4]]]. An approximately unital [[Banach algebra|Banach algebra]] $ A $ |
| + | is said to be semi-regular if it satisfies $ R ^ {* * } ( e ) = L ^ {* * } ( e ) $ | ||
| + | for all mixed identities $ e $. | ||
| + | (An element $ e \in A ^ {* * } $ | ||
| + | is called a mixed identity if it is simultaneously a right identity for the first Arens product and a left identity for the second Arens product, see [[Arens multiplication|Arens multiplication]].) He shows that an Arens-regular algebra is semi-regular and that any commutative approximately unital Banach algebra is semi-regular. | ||
The most comprehensive recent (1996) exposition is [[#References|[a7]]], which contains numerous further references. | The most comprehensive recent (1996) exposition is [[#References|[a7]]], which contains numerous further references. | ||
Revision as of 18:48, 5 April 2020
A normed algebra $ A $
is said to be Arens regular if the pair of intrinsically defined Arens products (introduced by R. Arens in [a1] and [a2]; cf. Arens multiplication) on the double dual space $ A ^ {* * } $
are identical. Since both Arens products extend the product on $ A $(
relative to the natural embedding mapping $ \kappa : A \rightarrow {A ^ {* * } } $),
a Banach algebra on a reflexive Banach space (cf. also Reflexive space) is Arens regular. S. Sherman has shown [a10] that the double dual of a $ C ^ {*} $-
algebra $ A $
has a natural interpretation as the von Neumann algebra generated by the universal $ * $-
representation of $ A $.
Hence $ C ^ {*} $-
algebras are always Arens regular.
It is easy to show that if $ A ^ {* * } $ is commutative under either Arens product, then $ A $ is Arens regular. The following fundamental result is due to J. Hennefeld [a5], based on work of J.S. Pym [a8] making use of Grothendieck's criterion for weak compactness.
The following conditions are equivalent for a Banach algebra $ A $:
a) $ A $ is Arens regular;
b) for each $ a \in A $ the adjoint $ {L _ {a} ^ {*} } : {A ^ {*} } \rightarrow {A ^ {*} } $ of the left regular representation is weakly compact;
c) for each $ a \in A $ the adjoint $ {R _ {a} ^ {*} } : {A ^ {*} } \rightarrow {A ^ {*} } $ of the right regular representation is weakly compact;
d) for any bounded sequences $ \{ a _ {n} \} _ {n \in \mathbf N } $ and $ \{ b _ {n} \} _ {n \in \mathbf N } $ in $ A $ and any $ \omega \in A ^ {*} $, the iterated limits
$$ {\lim\limits } _ { n } {\lim\limits } _ { m } \omega ( a _ {n} b _ {n} ) , \quad {\lim\limits } _ { m } {\lim\limits } _ { n } \omega ( a _ {n} b _ {n} ) $$
are equal when they both exist.
This theorem easily implies that subalgebras and quotient algebras (with respect to closed ideals) of Arens-regular algebras are Arens regular, as first noted in [a3].
Arens regularity is rare among general Banach algebras. N.J. Young [a11] has shown that for a locally compact group (cf. also Compact group; Locally compact skew-field) $ G $, $ L ^ {1} ( G ) $( or $ M ( G ) $) is Arens regular if and only if $ G $ is finite. P. Civin and B. Yood had proved this for Abelian groups in [a3]. In [a12] it is shown that the measure algebra (cf. Algebra of measures) $ M ( S ) $ of a locally compact semi-group $ S $ in which multiplication is at least singly continuous is Arens regular if and only if $ {\mathcal l} ^ {1} ( S ) $ is. These are, in turn, equivalent to either:
there do not exist sequences $ \{ u _ {n} \} $ and $ \{ v _ {m} \} $ in $ S $ such that the sets $ \{ {u _ {n} v _ {m} } : {m > n } \} $ and $ \{ {u _ {n} v _ {m} } : {m < n } \} $ are disjoint;
the semi-group operation can be extended to the Stone–Čech compactification $ \beta S $ of $ S $ as a discrete space.
In [a13], Young has proved that the algebra $ B _ {A} ( X ) $ of approximable operators (i.e., those uniformly approximable by finite-rank operators) on a Banach space $ X $ is regular if and only if $ X $ is reflexive (cf. Reflexive space). Hence, if the Banach algebra $ B ( X ) $ of all bounded linear operators on a Banach space $ X $ is Arens regular, then $ X $ must be reflexive. He also shows that there are reflexive Banach spaces $ X $ with $ B ( X ) $ not Arens regular.
Á. Rodriguez-Palacios [a9] has shown that any (even non-associative) continuous multiplication on a Banach space $ A $ is Arens regular if and only if every bounded linear mapping from $ A $ into $ A ^ {*} $ is weakly compact (cf. Weak topology). $ C ^ {*} $- algebras satisfy this criterion.
A weaker version of Arens regularity was introduced by M. Grosser [a4]. An approximately unital Banach algebra $ A $ is said to be semi-regular if it satisfies $ R ^ {* * } ( e ) = L ^ {* * } ( e ) $ for all mixed identities $ e $. (An element $ e \in A ^ {* * } $ is called a mixed identity if it is simultaneously a right identity for the first Arens product and a left identity for the second Arens product, see Arens multiplication.) He shows that an Arens-regular algebra is semi-regular and that any commutative approximately unital Banach algebra is semi-regular.
The most comprehensive recent (1996) exposition is [a7], which contains numerous further references.
References
| [a1] | R. Arens, "Operations induced in function classes" Monatsh. Math. , 55 (1951) pp. 1–19 |
| [a2] | R. Arens, "The adjoint of a bilinear operation" Proc. Amer. Math. Soc. , 2 (1951) pp. 839–848 |
| [a3] | P. Civin, B. Yood, "The second conjugate space of a Banach algebra as an algebra" Pacific J. Math. , 11 (1961) pp. 847–870 |
| [a4] | M. Grosser, "Arens semiregular Banach algebras" Monatsh. Math. , 98 : 1 (1984) pp. 41–52 |
| [a5] | J.O. Hennefeld, "A note on the Arens products" Pacific J. Math. , 26 (1968) pp. 115–119 |
| [a6] | S. Kaijser, "On Banach modules I" Math. Proc. Cambridge Philos. Soc. , 90 : 3 (1981) pp. 423–444 |
| [a7] | T.W. Palmer, "Banach algebras and the general theory of  -algebras I" , Encycl. Math. Appl. , 49 , Cambridge Univ. Press (1994) -algebras I" , Encycl. Math. Appl. , 49 , Cambridge Univ. Press (1994) |
| [a8] | J.S. Pym, "The convolution of functionals on spaces of bounded functions" Proc. London Math. Soc. (3) , 15 (1965) pp. 84–104 |
| [a9] | Á. Rodriguez-Palacios, "A note on Arens regularity" Quart. J. Math. Oxford Ser. (2) , 38 : 149 (1987) pp. 1991–1993 |
| [a10] | S. Sherman, "The second adjoint of a 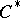 -algebra" , Proc. Internat. Congress Math. Cambridge, I (1950) pp. 470 -algebra" , Proc. Internat. Congress Math. Cambridge, I (1950) pp. 470 |
| [a11] | N.J. Young, "The irregularity of multiplication in group algebras" Quart. J. Math. Oxford Ser. (2) , 24 (1973) pp. 59–62 |
| [a12] | N.J. Young, "Semigroup algebras having regular multiplication" Studia Math. , 47 (1973) pp. 191–196 |
| [a13] | N.J. Young, "Periodicity of functionals and representations of normed algebras on reflexive spaces" Proc. Edinburgh Math. Soc. (2) , 20 : 2 (1976–77) pp. 99–120 |
Arens regularity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Arens_regularity&oldid=45217