Difference between revisions of "A-operation"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | a0100203.png | ||
| + | $#A+1 = 14 n = 1 | ||
| + | $#C+1 = 14 : ~/encyclopedia/old_files/data/A010/A.0100020 \BMI \FfA\EMI\AAhoperation, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | ''operation $ {\mathcal A} $'' | |
| − | + | A set-theoretical operation, discovered by P.S. Aleksandrov [[#References|[1]]] (see also [[#References|[2]]], [[#References|[3]]]). Let $ \{ E _ {n _ {1} \dots n _ {k} } \} $ | |
| + | be a system of sets indexed by all finite sequences of natural numbers. The set | ||
| − | The use of the | + | $$ |
| + | P = \cup _ {n _ {1} \dots n _ {k} , . . } \cap _ { k=1 } ^ \infty E _ {n _ {1} {} \dots n _ {k} } , | ||
| + | $$ | ||
| + | |||
| + | where the union is over all infinite sequences of natural numbers, is called the result of the $ {\mathcal A} $- | ||
| + | operation applied to the system $ \{ E _ {n _ {1} \dots n _ {k} } \} $. | ||
| + | |||
| + | The use of the $ {\mathcal A} $- | ||
| + | operation for the system of intervals of the number line gives sets (called $ {\mathcal A} $- | ||
| + | sets in honour of Aleksandrov) which need not be Borel sets (see [[A-set| $ {\mathcal A} $- | ||
| + | set]]; [[Descriptive set theory|Descriptive set theory]]). The $ {\mathcal A} $- | ||
| + | operation is stronger than the operation of countable union and countable intersection, and is idempotent. With respect to $ {\mathcal A} $- | ||
| + | operations, the [[Baire property|Baire property]] (of subsets of an arbitrary topological space) and the property of being Lebesgue measurable are invariant. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> P.S. Aleksandrov, ''C.R. Acad. Sci. Paris'' , '''162''' (1916) pp. 323–325</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P.S. Aleksandrov, "Theory of functions of a real variable and the theory of topological spaces" , Moscow (1978) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.N. Kolmogorov, "P.S. Aleksandrov and the theory of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010020/a01002013.png" />-operations" ''Uspekhi Mat. Nauk'' , '''21''' : 4 (1966) pp. 275–278 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.Ya. Suslin, ''C.R. Acad. Sci. Paris'' , '''164''' (1917) pp. 88–91</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> N.N. Luzin, , ''Collected works'' , '''2''' , Moscow (1958) pp. 284 (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> K. Kuratowski, "Topology" , '''1–2''' , Acad. Press (1966–1968) (Translated from French)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> P.S. Aleksandrov, ''C.R. Acad. Sci. Paris'' , '''162''' (1916) pp. 323–325</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P.S. Aleksandrov, "Theory of functions of a real variable and the theory of topological spaces" , Moscow (1978) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A.N. Kolmogorov, "P.S. Aleksandrov and the theory of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010020/a01002013.png" />-operations" ''Uspekhi Mat. Nauk'' , '''21''' : 4 (1966) pp. 275–278 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.Ya. Suslin, ''C.R. Acad. Sci. Paris'' , '''164''' (1917) pp. 88–91</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> N.N. Luzin, , ''Collected works'' , '''2''' , Moscow (1958) pp. 284 (In Russian)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> K. Kuratowski, "Topology" , '''1–2''' , Acad. Press (1966–1968) (Translated from French)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | The | + | The $ {\mathcal A} $- |
| + | operation is in the West usually attributed to M.Ya. Suslin [[#References|[4]]], and is therefore also called the Suslin operation, the Suslin $ {\mathcal A} $- | ||
| + | operation or the Suslin operation $ {\mathcal A} $. | ||
| + | $ {\mathcal A} $- | ||
| + | sets are usually called analytic sets. | ||
Revision as of 18:47, 5 April 2020
operation $ {\mathcal A} $
A set-theoretical operation, discovered by P.S. Aleksandrov [1] (see also [2], [3]). Let $ \{ E _ {n _ {1} \dots n _ {k} } \} $ be a system of sets indexed by all finite sequences of natural numbers. The set
$$ P = \cup _ {n _ {1} \dots n _ {k} , . . } \cap _ { k=1 } ^ \infty E _ {n _ {1} {} \dots n _ {k} } , $$
where the union is over all infinite sequences of natural numbers, is called the result of the $ {\mathcal A} $- operation applied to the system $ \{ E _ {n _ {1} \dots n _ {k} } \} $.
The use of the $ {\mathcal A} $- operation for the system of intervals of the number line gives sets (called $ {\mathcal A} $- sets in honour of Aleksandrov) which need not be Borel sets (see $ {\mathcal A} $- set; Descriptive set theory). The $ {\mathcal A} $- operation is stronger than the operation of countable union and countable intersection, and is idempotent. With respect to $ {\mathcal A} $- operations, the Baire property (of subsets of an arbitrary topological space) and the property of being Lebesgue measurable are invariant.
References
| [1] | P.S. Aleksandrov, C.R. Acad. Sci. Paris , 162 (1916) pp. 323–325 |
| [2] | P.S. Aleksandrov, "Theory of functions of a real variable and the theory of topological spaces" , Moscow (1978) (In Russian) |
| [3] | A.N. Kolmogorov, "P.S. Aleksandrov and the theory of 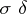 -operations" Uspekhi Mat. Nauk , 21 : 4 (1966) pp. 275–278 (In Russian) -operations" Uspekhi Mat. Nauk , 21 : 4 (1966) pp. 275–278 (In Russian) |
| [4] | M.Ya. Suslin, C.R. Acad. Sci. Paris , 164 (1917) pp. 88–91 |
| [5] | N.N. Luzin, , Collected works , 2 , Moscow (1958) pp. 284 (In Russian) |
| [6] | K. Kuratowski, "Topology" , 1–2 , Acad. Press (1966–1968) (Translated from French) |
Comments
The $ {\mathcal A} $- operation is in the West usually attributed to M.Ya. Suslin [4], and is therefore also called the Suslin operation, the Suslin $ {\mathcal A} $- operation or the Suslin operation $ {\mathcal A} $. $ {\mathcal A} $- sets are usually called analytic sets.
A-operation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=A-operation&oldid=45193