Difference between revisions of "Algebraic system, automorphism of an"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | a0116602.png | ||
| + | $#A+1 = 141 n = 1 | ||
| + | $#C+1 = 141 : ~/encyclopedia/old_files/data/A011/A.0101660 Algebraic system, automorphism of an | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | An isomorphic mapping of an algebraic system onto itself. An automorphism of an $ \Omega $- | |
| + | system $ \mathbf A = \langle A, \Omega \rangle $ | ||
| + | is a one-to-one mapping $ \phi $ | ||
| + | of the set $ A $ | ||
| + | onto itself having the following properties: | ||
| − | + | $$ \tag{1 } | |
| + | \phi ( F ( x _ {1} \dots x _ {n} ) ) = F ( \phi ( x _ {1} ) \dots | ||
| + | \phi ( x _ {n} ) ) , | ||
| + | $$ | ||
| − | + | $$ \tag{2 } | |
| + | P ( x _ {1} \dots x _ {m} ) \iff P ( \phi ( x _ {1} ) \dots \phi ( x _ {m} ) ), | ||
| + | $$ | ||
| − | + | for all $ x _ {1} , x _ {2} \dots $ | |
| + | from $ A $ | ||
| + | and for all $ F, P $ | ||
| + | from $ \Omega $. | ||
| + | In other words, an automorphism of an $ \Omega $- | ||
| + | system $ \mathbf A $ | ||
| + | is an isomorphic mapping of the system $ \mathbf A $ | ||
| + | onto itself. Let $ G $ | ||
| + | be the set of all automorphisms of the system $ \mathbf A $. | ||
| + | If $ \phi \in G $, | ||
| + | the inverse mapping $ \phi ^ {-1} $ | ||
| + | also has the properties (1) and (2), and for this reason $ \phi ^ {-1} \in G $. | ||
| + | The product $ \alpha = \phi \psi $ | ||
| + | of two automorphisms $ \phi , \psi $ | ||
| + | of the system $ \mathbf A $, | ||
| + | defined by the formula $ \alpha (x) = \psi ( \phi (x) ) $, | ||
| + | $ x \in A $, | ||
| + | is again an automorphism of the system $ \mathbf A $. | ||
| + | Since multiplication of mappings is associative, $ \langle G, \cdot , {} ^ {-1} \rangle $ | ||
| + | is a group, known as the group of all automorphisms of the system $ \mathbf A $; | ||
| + | it is denoted by $ \mathop{\rm Aut} ( \mathbf A ) $. | ||
| + | The subgroups of the group $ \mathop{\rm Aut} ( \mathbf A ) $ | ||
| + | are simply called automorphism groups of the system $ \mathbf A $. | ||
| − | + | Let $ \phi $ | |
| + | be an automorphism of the system $ \mathbf A $ | ||
| + | and let $ \theta $ | ||
| + | be a congruence of this system. Putting | ||
| − | + | $$ | |
| + | ( x , y ) \in \theta _ \phi \iff ( \phi ^ {-1} ( x ) ,\ | ||
| + | \phi ^ {-1} ( y ) ) \in \theta ,\ x , y \in \mathbf A , | ||
| + | $$ | ||
| − | + | one again obtains a congruence $ \theta _ \phi $ | |
| + | of the system $ \mathbf A $. | ||
| + | The automorphism $ \phi $ | ||
| + | is known as an IC-automorphism if $ \theta _ \phi = \theta $ | ||
| + | for any congruence $ \theta $ | ||
| + | of the system $ \mathbf A $. | ||
| + | The set $ \mathop{\rm IC} ( \mathbf A ) $ | ||
| + | of all IC-automorphisms of the system $ \mathbf A $ | ||
| + | is a normal subgroup of the group $ \mathop{\rm Aut} ( \mathbf A ) $, | ||
| + | and the quotient group $ \mathop{\rm Aut} ( \mathbf A ) / \mathop{\rm IC} ( \mathbf A ) $ | ||
| + | is isomorphic to an automorphism group of the lattice of all congruences of the system $ \mathbf A $[[#References|[1]]]. In particular, any inner automorphism $ x \rightarrow a ^ {-1} xa $ | ||
| + | of a group defined by a fixed element $ a $ | ||
| + | of this group is an IC-automorphism. However, the example of a cyclic group of prime order shows that not all IC-automorphisms of a group are inner. | ||
| − | + | Let $ \mathfrak K $ | |
| + | be a non-trivial variety of $ \Omega $- | ||
| + | systems or any other class of $ \Omega $- | ||
| + | systems comprising free systems of any (non-zero) rank. An automorphism $ \phi $ | ||
| + | of a system $ \mathbf A $ | ||
| + | of the class $ \mathfrak K $ | ||
| + | is called an I-automorphism if there exists a term $ f _ \phi (x _ {1} \dots x _ {n} ) $ | ||
| + | of the signature $ \Omega $, | ||
| + | in the unknowns $ x _ {1} \dots x _ {n} $, | ||
| + | for which: 1) in the system $ \mathbf A $ | ||
| + | there exist elements $ a _ {2} \dots a _ {n} $ | ||
| + | such that for each element $ x \in A $ | ||
| + | the equality | ||
| − | + | $$ | |
| + | \phi ( x ) = f _ \phi ( x , a _ {2} \dots a _ {n} ) | ||
| + | $$ | ||
| − | is | + | is valid; and 2) for any system $ \mathbf B $ |
| + | of the class $ \mathfrak K $ | ||
| + | the mapping | ||
| − | + | $$ | |
| + | x \rightarrow f _ \phi ( x , x _ {2} \dots x _ {n} ) | ||
| + | \ ( x \in B ) | ||
| + | $$ | ||
| − | + | is an automorphism of this system for any arbitrary selection of elements $ x _ {2} \dots x _ {n} $ | |
| + | in the system $ \mathbf B $. | ||
| + | The set $ \textrm{ I } ( \mathbf A ) $ | ||
| + | of all I-automorphisms for each system $ \mathbf A $ | ||
| + | of the class $ \mathfrak K $ | ||
| + | is a normal subgroup of the group $ \mathop{\rm Aut} ( \mathbf A ) $. | ||
| + | In the class $ \mathfrak K $ | ||
| + | of all groups the concept of an I-automorphism coincides with the concept of an inner automorphism of the group [[#References|[2]]]. For the more general concept of a formula automorphism of $ \Omega $- | ||
| + | systems, see [[#References|[3]]]. | ||
| − | + | Let $ \mathbf A $ | |
| + | be an algebraic system. By replacing each basic operation $ F $ | ||
| + | in $ \mathbf A $ | ||
| + | by the predicate | ||
| − | one obtains the so-called model | + | $$ |
| + | R ( x _ {1} \dots x _ {n} , y ) \iff \ | ||
| + | F ( x _ {1} \dots x _ {n} ) = y | ||
| + | $$ | ||
| + | |||
| + | $$ | ||
| + | ( x _ {1} \dots x _ {n} , y \in A ) , | ||
| + | $$ | ||
| + | |||
| + | one obtains the so-called model $ \mathbf A ^ {*} $ | ||
| + | which represents the system $ \mathbf A $. | ||
| + | The equality $ \mathop{\rm Aut} ( \mathbf A ^ {*} ) = \mathop{\rm Aut} ( \mathbf A ) $ | ||
| + | is valid. If the systems $ \mathbf A = \langle A, \Omega \rangle $ | ||
| + | and $ \mathbf A ^ \prime = \langle A , \Omega ^ \prime \rangle $ | ||
| + | have a common carrier $ A $, | ||
| + | and if $ \Omega \subset \Omega ^ \prime $, | ||
| + | then $ \mathop{\rm Aut} ( \mathbf A ) \supseteq \mathop{\rm Aut} ( \mathbf A ^ \prime ) $. | ||
| + | If the $ \Omega $- | ||
| + | system $ \mathbf A $ | ||
| + | with a finite number of generators is finitely approximable, the group $ \mathop{\rm Aut} ( \mathbf A ) $ | ||
| + | is also finitely approximable (cf. [[#References|[1]]]). Let $ \mathfrak K $ | ||
| + | be a class of $ \Omega $- | ||
| + | systems and let $ \mathop{\rm Aut} ( \mathfrak K ) $ | ||
| + | be the class of all isomorphic copies of the groups $ \mathop{\rm Aut} ( \mathbf A ) $, | ||
| + | $ \mathbf A \in \mathfrak K $, | ||
| + | and let $ \mathop{\rm SAut} ( \mathfrak K ) $ | ||
| + | be the class of subgroups of groups from the class $ \mathop{\rm Aut} ( \mathfrak K ) $. | ||
| + | The class $ \mathop{\rm SAut} ( \mathfrak K ) $ | ||
| + | consists of groups which are isomorphically imbeddable into the groups $ \mathop{\rm Aut} ( \mathbf A ) $, | ||
| + | $ \mathbf A \in \mathfrak K $. | ||
The following two problems arose in the study of automorphism groups of algebraic systems. | The following two problems arose in the study of automorphism groups of algebraic systems. | ||
| − | 1) Given a class | + | 1) Given a class $ \mathfrak K $ |
| + | of $ \Omega $- | ||
| + | systems, what can one say about the classes $ \mathop{\rm Aut} ( \mathfrak K ) $ | ||
| + | and $ \mathop{\rm SAut} ( \mathfrak K ) $? | ||
| − | 2) Let an (abstract) class | + | 2) Let an (abstract) class $ K $ |
| + | of groups be given. Does there exist a class $ \mathfrak K $ | ||
| + | of $ \Omega $- | ||
| + | systems with a given signature $ \Omega $ | ||
| + | such that $ K = \mathop{\rm Aut} ( \mathfrak K ) $ | ||
| + | or even $ K = \mathop{\rm SAut} ( \mathfrak K ) $? | ||
| + | It has been proved that for any axiomatizable class $ \mathfrak K $ | ||
| + | of models the class of groups $ \mathop{\rm SAut} ( \mathfrak K ) $ | ||
| + | is universally axiomatizable [[#References|[1]]]. It has also been proved [[#References|[1]]], [[#References|[4]]] that if $ \mathfrak K $ | ||
| + | is an axiomatizable class of models comprising infinite models, if $ \langle B, \leq \rangle $ | ||
| + | is a totally ordered set and if $ \mathbf G $ | ||
| + | is an automorphism group of the model $ \langle B, \leq \rangle $, | ||
| + | then there exists a model $ \mathbf A \in \mathfrak K $ | ||
| + | such that $ A \supseteq B $, | ||
| + | and for each element $ g \in G $ | ||
| + | there exists an automorphism $ \phi $ | ||
| + | of the system $ \mathbf A $ | ||
| + | such that $ g(x) = \phi (x) $ | ||
| + | for all $ x \in B $. | ||
| + | The group $ G $ | ||
| + | is called 1) universal if $ G \in \mathop{\rm SAut} ( \mathfrak K ) $ | ||
| + | for any axiomatizable class $ \mathfrak K $ | ||
| + | of models comprising infinite models; and 2) a group of ordered automorphisms of an ordered group $ \mathbf H $( | ||
| + | cf. [[Totally ordered group|Totally ordered group]]) if $ \mathbf G $ | ||
| + | is isomorphic to some automorphism group of the group $ \mathbf H $ | ||
| + | which preserves the given total order $ \leq $ | ||
| + | of this group (i.e. $ a \leq b \Rightarrow \phi (a) \leq \phi (b) $ | ||
| + | for all $ a, b \in H $, | ||
| + | $ \phi \in G $). | ||
| − | Let | + | Let $ l $ |
| + | be the class of totally ordered sets $ \langle M, \leq \rangle $, | ||
| + | let $ \mathfrak U $ | ||
| + | be the class of universal groups, let RO be the class of right-ordered groups and let OA be the class of ordered automorphism groups of free Abelian groups. Then [[#References|[4]]], [[#References|[5]]], [[#References|[6]]]: | ||
| − | + | $$ | |
| + | \mathop{\rm SAut} ( l ) = \mathfrak U = \mathop{\rm RO} = \mathop{\rm OA} . | ||
| + | $$ | ||
| − | Each group is isomorphic to the group of all automorphisms of some | + | Each group is isomorphic to the group of all automorphisms of some $ \Omega $- |
| + | algebra. If $ \mathfrak K $ | ||
| + | is the class of all rings, $ \mathop{\rm Aut} ( \mathfrak K ) $ | ||
| + | is the class of all groups [[#References|[1]]]. However, if $ \mathfrak K $ | ||
| + | is the class of all groups, $ \mathop{\rm Aut} ( \mathfrak K ) \neq \mathfrak K $; | ||
| + | for example, the cyclic groups $ \mathbf C _ {3} , \mathbf C _ {5} , \mathbf C _ {7} $ | ||
| + | of the respective orders 3, 5 and 7 do not belong to the class $ \mathop{\rm Aut} ( \mathfrak K ) $. | ||
| + | There is also no topological group whose group of all topological automorphisms is isomorphic to $ \mathbf C _ {5} $[[#References|[7]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> B.I. Plotkin, "Groups of automorphisms of algebraic systems" , Wolters-Noordhoff (1972)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B. Csákány, "Inner automorphisms of universal algebras" ''Publ. Math. Debrecen'' , '''12''' (1965) pp. 331–333</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Grant, "Automorphisms definable by formulas" ''Pacific J. Math.'' , '''44''' (1973) pp. 107–115</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.O. Rabin, "Universal groups of automorphisms of models" , ''Theory of models'' , North-Holland (1965) pp. 274–284</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> P.M. Cohn, "Groups of order automorphisms of ordered sets" ''Mathematika'' , '''4''' (1957) pp. 41–50</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> D.M. Smirnov, "Right-ordered groups" ''Algebra i Logika'' , '''5''' : 6 (1966) pp. 41–59 (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> R.J. Wille, "The existence of a topological group with automorphism group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011660/a011660148.png" />" ''Quart. J. Math. Oxford (2)'' , '''18''' (1967) pp. 53–57</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> B.I. Plotkin, "Groups of automorphisms of algebraic systems" , Wolters-Noordhoff (1972)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> B. Csákány, "Inner automorphisms of universal algebras" ''Publ. Math. Debrecen'' , '''12''' (1965) pp. 331–333</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Grant, "Automorphisms definable by formulas" ''Pacific J. Math.'' , '''44''' (1973) pp. 107–115</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.O. Rabin, "Universal groups of automorphisms of models" , ''Theory of models'' , North-Holland (1965) pp. 274–284</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> P.M. Cohn, "Groups of order automorphisms of ordered sets" ''Mathematika'' , '''4''' (1957) pp. 41–50</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> D.M. Smirnov, "Right-ordered groups" ''Algebra i Logika'' , '''5''' : 6 (1966) pp. 41–59 (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> R.J. Wille, "The existence of a topological group with automorphism group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a011/a011660/a011660148.png" />" ''Quart. J. Math. Oxford (2)'' , '''18''' (1967) pp. 53–57</TD></TR></table> | ||
Revision as of 16:10, 1 April 2020
An isomorphic mapping of an algebraic system onto itself. An automorphism of an $ \Omega $-
system $ \mathbf A = \langle A, \Omega \rangle $
is a one-to-one mapping $ \phi $
of the set $ A $
onto itself having the following properties:
$$ \tag{1 } \phi ( F ( x _ {1} \dots x _ {n} ) ) = F ( \phi ( x _ {1} ) \dots \phi ( x _ {n} ) ) , $$
$$ \tag{2 } P ( x _ {1} \dots x _ {m} ) \iff P ( \phi ( x _ {1} ) \dots \phi ( x _ {m} ) ), $$
for all $ x _ {1} , x _ {2} \dots $ from $ A $ and for all $ F, P $ from $ \Omega $. In other words, an automorphism of an $ \Omega $- system $ \mathbf A $ is an isomorphic mapping of the system $ \mathbf A $ onto itself. Let $ G $ be the set of all automorphisms of the system $ \mathbf A $. If $ \phi \in G $, the inverse mapping $ \phi ^ {-1} $ also has the properties (1) and (2), and for this reason $ \phi ^ {-1} \in G $. The product $ \alpha = \phi \psi $ of two automorphisms $ \phi , \psi $ of the system $ \mathbf A $, defined by the formula $ \alpha (x) = \psi ( \phi (x) ) $, $ x \in A $, is again an automorphism of the system $ \mathbf A $. Since multiplication of mappings is associative, $ \langle G, \cdot , {} ^ {-1} \rangle $ is a group, known as the group of all automorphisms of the system $ \mathbf A $; it is denoted by $ \mathop{\rm Aut} ( \mathbf A ) $. The subgroups of the group $ \mathop{\rm Aut} ( \mathbf A ) $ are simply called automorphism groups of the system $ \mathbf A $.
Let $ \phi $ be an automorphism of the system $ \mathbf A $ and let $ \theta $ be a congruence of this system. Putting
$$ ( x , y ) \in \theta _ \phi \iff ( \phi ^ {-1} ( x ) ,\ \phi ^ {-1} ( y ) ) \in \theta ,\ x , y \in \mathbf A , $$
one again obtains a congruence $ \theta _ \phi $ of the system $ \mathbf A $. The automorphism $ \phi $ is known as an IC-automorphism if $ \theta _ \phi = \theta $ for any congruence $ \theta $ of the system $ \mathbf A $. The set $ \mathop{\rm IC} ( \mathbf A ) $ of all IC-automorphisms of the system $ \mathbf A $ is a normal subgroup of the group $ \mathop{\rm Aut} ( \mathbf A ) $, and the quotient group $ \mathop{\rm Aut} ( \mathbf A ) / \mathop{\rm IC} ( \mathbf A ) $ is isomorphic to an automorphism group of the lattice of all congruences of the system $ \mathbf A $[1]. In particular, any inner automorphism $ x \rightarrow a ^ {-1} xa $ of a group defined by a fixed element $ a $ of this group is an IC-automorphism. However, the example of a cyclic group of prime order shows that not all IC-automorphisms of a group are inner.
Let $ \mathfrak K $ be a non-trivial variety of $ \Omega $- systems or any other class of $ \Omega $- systems comprising free systems of any (non-zero) rank. An automorphism $ \phi $ of a system $ \mathbf A $ of the class $ \mathfrak K $ is called an I-automorphism if there exists a term $ f _ \phi (x _ {1} \dots x _ {n} ) $ of the signature $ \Omega $, in the unknowns $ x _ {1} \dots x _ {n} $, for which: 1) in the system $ \mathbf A $ there exist elements $ a _ {2} \dots a _ {n} $ such that for each element $ x \in A $ the equality
$$ \phi ( x ) = f _ \phi ( x , a _ {2} \dots a _ {n} ) $$
is valid; and 2) for any system $ \mathbf B $ of the class $ \mathfrak K $ the mapping
$$ x \rightarrow f _ \phi ( x , x _ {2} \dots x _ {n} ) \ ( x \in B ) $$
is an automorphism of this system for any arbitrary selection of elements $ x _ {2} \dots x _ {n} $ in the system $ \mathbf B $. The set $ \textrm{ I } ( \mathbf A ) $ of all I-automorphisms for each system $ \mathbf A $ of the class $ \mathfrak K $ is a normal subgroup of the group $ \mathop{\rm Aut} ( \mathbf A ) $. In the class $ \mathfrak K $ of all groups the concept of an I-automorphism coincides with the concept of an inner automorphism of the group [2]. For the more general concept of a formula automorphism of $ \Omega $- systems, see [3].
Let $ \mathbf A $ be an algebraic system. By replacing each basic operation $ F $ in $ \mathbf A $ by the predicate
$$ R ( x _ {1} \dots x _ {n} , y ) \iff \ F ( x _ {1} \dots x _ {n} ) = y $$
$$ ( x _ {1} \dots x _ {n} , y \in A ) , $$
one obtains the so-called model $ \mathbf A ^ {*} $ which represents the system $ \mathbf A $. The equality $ \mathop{\rm Aut} ( \mathbf A ^ {*} ) = \mathop{\rm Aut} ( \mathbf A ) $ is valid. If the systems $ \mathbf A = \langle A, \Omega \rangle $ and $ \mathbf A ^ \prime = \langle A , \Omega ^ \prime \rangle $ have a common carrier $ A $, and if $ \Omega \subset \Omega ^ \prime $, then $ \mathop{\rm Aut} ( \mathbf A ) \supseteq \mathop{\rm Aut} ( \mathbf A ^ \prime ) $. If the $ \Omega $- system $ \mathbf A $ with a finite number of generators is finitely approximable, the group $ \mathop{\rm Aut} ( \mathbf A ) $ is also finitely approximable (cf. [1]). Let $ \mathfrak K $ be a class of $ \Omega $- systems and let $ \mathop{\rm Aut} ( \mathfrak K ) $ be the class of all isomorphic copies of the groups $ \mathop{\rm Aut} ( \mathbf A ) $, $ \mathbf A \in \mathfrak K $, and let $ \mathop{\rm SAut} ( \mathfrak K ) $ be the class of subgroups of groups from the class $ \mathop{\rm Aut} ( \mathfrak K ) $. The class $ \mathop{\rm SAut} ( \mathfrak K ) $ consists of groups which are isomorphically imbeddable into the groups $ \mathop{\rm Aut} ( \mathbf A ) $, $ \mathbf A \in \mathfrak K $.
The following two problems arose in the study of automorphism groups of algebraic systems.
1) Given a class $ \mathfrak K $ of $ \Omega $- systems, what can one say about the classes $ \mathop{\rm Aut} ( \mathfrak K ) $ and $ \mathop{\rm SAut} ( \mathfrak K ) $?
2) Let an (abstract) class $ K $ of groups be given. Does there exist a class $ \mathfrak K $ of $ \Omega $- systems with a given signature $ \Omega $ such that $ K = \mathop{\rm Aut} ( \mathfrak K ) $ or even $ K = \mathop{\rm SAut} ( \mathfrak K ) $? It has been proved that for any axiomatizable class $ \mathfrak K $ of models the class of groups $ \mathop{\rm SAut} ( \mathfrak K ) $ is universally axiomatizable [1]. It has also been proved [1], [4] that if $ \mathfrak K $ is an axiomatizable class of models comprising infinite models, if $ \langle B, \leq \rangle $ is a totally ordered set and if $ \mathbf G $ is an automorphism group of the model $ \langle B, \leq \rangle $, then there exists a model $ \mathbf A \in \mathfrak K $ such that $ A \supseteq B $, and for each element $ g \in G $ there exists an automorphism $ \phi $ of the system $ \mathbf A $ such that $ g(x) = \phi (x) $ for all $ x \in B $. The group $ G $ is called 1) universal if $ G \in \mathop{\rm SAut} ( \mathfrak K ) $ for any axiomatizable class $ \mathfrak K $ of models comprising infinite models; and 2) a group of ordered automorphisms of an ordered group $ \mathbf H $( cf. Totally ordered group) if $ \mathbf G $ is isomorphic to some automorphism group of the group $ \mathbf H $ which preserves the given total order $ \leq $ of this group (i.e. $ a \leq b \Rightarrow \phi (a) \leq \phi (b) $ for all $ a, b \in H $, $ \phi \in G $).
Let $ l $ be the class of totally ordered sets $ \langle M, \leq \rangle $, let $ \mathfrak U $ be the class of universal groups, let RO be the class of right-ordered groups and let OA be the class of ordered automorphism groups of free Abelian groups. Then [4], [5], [6]:
$$ \mathop{\rm SAut} ( l ) = \mathfrak U = \mathop{\rm RO} = \mathop{\rm OA} . $$
Each group is isomorphic to the group of all automorphisms of some $ \Omega $- algebra. If $ \mathfrak K $ is the class of all rings, $ \mathop{\rm Aut} ( \mathfrak K ) $ is the class of all groups [1]. However, if $ \mathfrak K $ is the class of all groups, $ \mathop{\rm Aut} ( \mathfrak K ) \neq \mathfrak K $; for example, the cyclic groups $ \mathbf C _ {3} , \mathbf C _ {5} , \mathbf C _ {7} $ of the respective orders 3, 5 and 7 do not belong to the class $ \mathop{\rm Aut} ( \mathfrak K ) $. There is also no topological group whose group of all topological automorphisms is isomorphic to $ \mathbf C _ {5} $[7].
References
| [1] | B.I. Plotkin, "Groups of automorphisms of algebraic systems" , Wolters-Noordhoff (1972) |
| [2] | B. Csákány, "Inner automorphisms of universal algebras" Publ. Math. Debrecen , 12 (1965) pp. 331–333 |
| [3] | J. Grant, "Automorphisms definable by formulas" Pacific J. Math. , 44 (1973) pp. 107–115 |
| [4] | M.O. Rabin, "Universal groups of automorphisms of models" , Theory of models , North-Holland (1965) pp. 274–284 |
| [5] | P.M. Cohn, "Groups of order automorphisms of ordered sets" Mathematika , 4 (1957) pp. 41–50 |
| [6] | D.M. Smirnov, "Right-ordered groups" Algebra i Logika , 5 : 6 (1966) pp. 41–59 (In Russian) |
| [7] | R.J. Wille, "The existence of a topological group with automorphism group 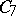 " Quart. J. Math. Oxford (2) , 18 (1967) pp. 53–57 " Quart. J. Math. Oxford (2) , 18 (1967) pp. 53–57 |
Algebraic system, automorphism of an. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Algebraic_system,_automorphism_of_an&oldid=45065