Difference between revisions of "Action of a group on a manifold"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | a0105501.png | ||
| + | $#A+1 = 76 n = 1 | ||
| + | $#C+1 = 76 : ~/encyclopedia/old_files/data/A010/A.0100550 Action of a group on a manifold | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | The best-studied case of the general concept of the action of a group on a space. A topological group $ G $ | |
| + | acts on a space $ X $ | ||
| + | if to each $ g \in G $ | ||
| + | there corresponds a homeomorphism $ \phi _ {g} $ | ||
| + | of $ X $( | ||
| + | onto itself) satisfying the following conditions: 1) $ \phi _ {g} \cdot \phi _ {h} = \phi _ {gh} $; | ||
| + | 2) for the unit element $ e \in G $ | ||
| + | the mapping $ \phi _ {e} $ | ||
| + | is the identity homeomorphism; and 3) the mapping $ \phi : G \times X \rightarrow X $, | ||
| + | $ \phi (g, x) = \phi _ {g} (x) $ | ||
| + | is continuous. If $ X $ | ||
| + | and $ G $ | ||
| + | have supplementary structures, the actions of $ G $ | ||
| + | which are compatible with such structures are of special interest; thus, if $ X $ | ||
| + | is a differentiable manifold and $ G $ | ||
| + | is a Lie group, the mapping $ \phi $ | ||
| + | is usually assumed to be differentiable. | ||
| − | + | The set $ \{ \phi _ {g} ( x _ {0} ) \} _ {g \in G } $ | |
| + | is called the orbit (trajectory) of the point $ x _ {0} \in X $ | ||
| + | with respect to the group $ G $; | ||
| + | the orbit space is denoted by $ X/G $, | ||
| + | and is also called the quotient space of the space $ X $ | ||
| + | with respect to the group $ G $. | ||
| + | An important example is the case when $ X $ | ||
| + | is a Lie group and $ G $ | ||
| + | is a subgroup; then $ X/G $ | ||
| + | is the corresponding [[Homogeneous space|homogeneous space]]. Classical examples include the spheres $ S ^ {n-1} = \textrm{ O } (n) / \textrm{ O } (n-1) $, | ||
| + | the Grassmann manifolds $ \textrm{ O } (n) / ( \textrm{ O } (m) \times \textrm{ O } (n-m) ) $, | ||
| + | and the Stiefel manifolds $ \textrm{ O } (n) / \textrm{ O } (m) $( | ||
| + | cf. [[Grassmann manifold|Grassmann manifold]]; [[Stiefel manifold|Stiefel manifold]]). Here, the orbit space is a manifold. This is usually not the case if the action of the group is not free, e.g. if the set $ X ^ {G} $ | ||
| + | of fixed points is non-empty. A free action of a group is an action for which $ g=e $ | ||
| + | follows if $ gx=x $ | ||
| + | for any $ x \in X $. | ||
| + | On the contrary, $ X ^ {G} $ | ||
| + | is a manifold if $ X $ | ||
| + | is a differentiable manifold and the action of $ G $ | ||
| + | is differentiable; this statement is valid for cohomology manifolds over $ \mathbf Z _ {p} $ | ||
| + | for $ G = \mathbf Z _ {p} $ | ||
| + | as well (Smith's theorem). | ||
| − | + | If $ G $ | |
| + | is a non-compact group, the space $ X/G $ | ||
| + | is usually inseparable, and this is why a study of individual trajectories and their mutual locations is of interest. The group $ G = \mathbf R $ | ||
| + | of real numbers acting on a differentiable manifold $ X $ | ||
| + | in a differentiable manner is a classical example. The study of such dynamical systems, which in terms of local coordinates is equivalent to the study of systems of ordinary differential equations, usually involves analytical methods. | ||
| − | If | + | If $ G $ |
| + | is a compact group, it is known that if $ X $ | ||
| + | is a manifold and if each $ g \in G $, | ||
| + | $ g \neq e $, | ||
| + | acts non-trivially on $ X $( | ||
| + | i.e. not according to the law $ (g, x) \rightarrow x $), | ||
| + | then $ G $ | ||
| + | is a Lie group [[#References|[8]]]. Accordingly, the main interest in the action of a compact group is the action of a Lie group. | ||
| − | + | Let $ G $ | |
| + | be a compact Lie group and let $ X $ | ||
| + | be a compact cohomology manifold. The following results are typical. A finite number of orbit types exists in $ X $, | ||
| + | and the neighbourhoods of an orbit look like a direct product (the slice theorem); the relations between the cohomology structures of the spaces $ X $, | ||
| + | $ X/G $ | ||
| + | and $ X ^ {G} $ | ||
| + | are of interest. | ||
| − | is | + | If $ G $ |
| + | is a compact Lie group, $ X $ | ||
| + | a differentiable manifold and if the action | ||
| − | Recent results (mid-1970s) mostly concern: 1) the determination of types of orbits with various supplementary assumptions concerning the group | + | $$ |
| + | \phi : G \times X \rightarrow X | ||
| + | $$ | ||
| + | |||
| + | is differentiable, then one naturally obtains the following equivalence relation: $ (X, \phi ) \sim ( X ^ { \prime } , \phi ^ \prime ) $ | ||
| + | if and only if it is possible to find an $ ( X ^ { \prime\prime } , \phi ^ {\prime\prime} ) $ | ||
| + | such that the boundary $ \partial X ^ { \prime\prime } $ | ||
| + | has the form $ \partial X ^ { \prime\prime } = X \cup X ^ { \prime } $ | ||
| + | and such that $ \phi ^ {\prime\prime} \mid _ {X} = \phi $, | ||
| + | $ \phi ^ {\prime\prime} \mid _ {X ^ { \prime } } = \phi ^ \prime $. | ||
| + | If the group $ G $ | ||
| + | acts freely, the equivalence classes can be found from the one-to-one correspondence with the bordisms $ \Omega _ {*} ( B _ {G} ) $ | ||
| + | of the classifying space $ B _ {G} $( | ||
| + | cf. [[Bordism|Bordism]]). | ||
| + | |||
| + | Recent results (mid-1970s) mostly concern: 1) the determination of types of orbits with various supplementary assumptions concerning the group $ G $ | ||
| + | and the manifold $ X $([[#References|[6]]]); 2) the classification of group actions; and 3) finding connections between global invariants of the manifold $ X $ | ||
| + | and local properties of the group actions of $ G $ | ||
| + | in a neighbourhood of fixed points of $ X ^ {G} $. | ||
| + | In solving these problems an important part is played by: methods of modern differential topology (e.g. surgery methods); $ K _ {G} $- | ||
| + | theory [[#References|[1]]], which is the analogue of $ K $- | ||
| + | theory for $ G $- | ||
| + | vector bundles; bordism and cobordism theories [[#References|[3]]]; and analytical methods of studying the action of the group $ G $ | ||
| + | based on the study of pseudo-differential operators in $ G $- | ||
| + | bundles [[#References|[2]]], [[#References|[7]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> M.F. Atiyah, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010550/a01055077.png" />-theory: lectures" , Benjamin (1967)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M.F. Atiyah, I.M. Singer, "The index of elliptic operators" ''Ann. of Math. (2)'' , '''87''' (1968) pp. 484–530</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.M. Bukhshtaber, A.S. Mishchenko, S.P. Novikov, "Formal groups and their role in the apparatus of algebraic topology" ''Russian Math. Surveys'' , '''26''' (1971) pp. 63–90 ''Uspekhi Mat. Nauk'' , '''26''' : 2 (1971) pp. 131–154</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> P.E. Conner, E.E. Floyd, "Differentiable periodic maps" , Springer (1964)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> G. Bredon, "Introduction to compact transformation groups" , Acad. Press (1972)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> W.Y. Hsiang, "Cohomology theory of topological transformation groups" , Springer (1975)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> D.B. Zagier, "Equivariant Pontryagin classes and applications to orbit spaces" , Springer (1972)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> , ''Proc. conf. transformation groups'' , Springer (1968)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> , ''Proc. 2-nd conf. compact transformation groups'' , Springer (1972)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> M.F. Atiyah, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010550/a01055077.png" />-theory: lectures" , Benjamin (1967)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M.F. Atiyah, I.M. Singer, "The index of elliptic operators" ''Ann. of Math. (2)'' , '''87''' (1968) pp. 484–530</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.M. Bukhshtaber, A.S. Mishchenko, S.P. Novikov, "Formal groups and their role in the apparatus of algebraic topology" ''Russian Math. Surveys'' , '''26''' (1971) pp. 63–90 ''Uspekhi Mat. Nauk'' , '''26''' : 2 (1971) pp. 131–154</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> P.E. Conner, E.E. Floyd, "Differentiable periodic maps" , Springer (1964)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> G. Bredon, "Introduction to compact transformation groups" , Acad. Press (1972)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> W.Y. Hsiang, "Cohomology theory of topological transformation groups" , Springer (1975)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> D.B. Zagier, "Equivariant Pontryagin classes and applications to orbit spaces" , Springer (1972)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> , ''Proc. conf. transformation groups'' , Springer (1968)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> , ''Proc. 2-nd conf. compact transformation groups'' , Springer (1972)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | |||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> T. Petrie, J.D. Randall, "Transformation groups on manifolds" , M. Dekker (1984)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> T. Petrie, J.D. Randall, "Transformation groups on manifolds" , M. Dekker (1984)</TD></TR></table> | ||
Revision as of 16:08, 1 April 2020
The best-studied case of the general concept of the action of a group on a space. A topological group $ G $
acts on a space $ X $
if to each $ g \in G $
there corresponds a homeomorphism $ \phi _ {g} $
of $ X $(
onto itself) satisfying the following conditions: 1) $ \phi _ {g} \cdot \phi _ {h} = \phi _ {gh} $;
2) for the unit element $ e \in G $
the mapping $ \phi _ {e} $
is the identity homeomorphism; and 3) the mapping $ \phi : G \times X \rightarrow X $,
$ \phi (g, x) = \phi _ {g} (x) $
is continuous. If $ X $
and $ G $
have supplementary structures, the actions of $ G $
which are compatible with such structures are of special interest; thus, if $ X $
is a differentiable manifold and $ G $
is a Lie group, the mapping $ \phi $
is usually assumed to be differentiable.
The set $ \{ \phi _ {g} ( x _ {0} ) \} _ {g \in G } $ is called the orbit (trajectory) of the point $ x _ {0} \in X $ with respect to the group $ G $; the orbit space is denoted by $ X/G $, and is also called the quotient space of the space $ X $ with respect to the group $ G $. An important example is the case when $ X $ is a Lie group and $ G $ is a subgroup; then $ X/G $ is the corresponding homogeneous space. Classical examples include the spheres $ S ^ {n-1} = \textrm{ O } (n) / \textrm{ O } (n-1) $, the Grassmann manifolds $ \textrm{ O } (n) / ( \textrm{ O } (m) \times \textrm{ O } (n-m) ) $, and the Stiefel manifolds $ \textrm{ O } (n) / \textrm{ O } (m) $( cf. Grassmann manifold; Stiefel manifold). Here, the orbit space is a manifold. This is usually not the case if the action of the group is not free, e.g. if the set $ X ^ {G} $ of fixed points is non-empty. A free action of a group is an action for which $ g=e $ follows if $ gx=x $ for any $ x \in X $. On the contrary, $ X ^ {G} $ is a manifold if $ X $ is a differentiable manifold and the action of $ G $ is differentiable; this statement is valid for cohomology manifolds over $ \mathbf Z _ {p} $ for $ G = \mathbf Z _ {p} $ as well (Smith's theorem).
If $ G $ is a non-compact group, the space $ X/G $ is usually inseparable, and this is why a study of individual trajectories and their mutual locations is of interest. The group $ G = \mathbf R $ of real numbers acting on a differentiable manifold $ X $ in a differentiable manner is a classical example. The study of such dynamical systems, which in terms of local coordinates is equivalent to the study of systems of ordinary differential equations, usually involves analytical methods.
If $ G $ is a compact group, it is known that if $ X $ is a manifold and if each $ g \in G $, $ g \neq e $, acts non-trivially on $ X $( i.e. not according to the law $ (g, x) \rightarrow x $), then $ G $ is a Lie group [8]. Accordingly, the main interest in the action of a compact group is the action of a Lie group.
Let $ G $ be a compact Lie group and let $ X $ be a compact cohomology manifold. The following results are typical. A finite number of orbit types exists in $ X $, and the neighbourhoods of an orbit look like a direct product (the slice theorem); the relations between the cohomology structures of the spaces $ X $, $ X/G $ and $ X ^ {G} $ are of interest.
If $ G $ is a compact Lie group, $ X $ a differentiable manifold and if the action
$$ \phi : G \times X \rightarrow X $$
is differentiable, then one naturally obtains the following equivalence relation: $ (X, \phi ) \sim ( X ^ { \prime } , \phi ^ \prime ) $ if and only if it is possible to find an $ ( X ^ { \prime\prime } , \phi ^ {\prime\prime} ) $ such that the boundary $ \partial X ^ { \prime\prime } $ has the form $ \partial X ^ { \prime\prime } = X \cup X ^ { \prime } $ and such that $ \phi ^ {\prime\prime} \mid _ {X} = \phi $, $ \phi ^ {\prime\prime} \mid _ {X ^ { \prime } } = \phi ^ \prime $. If the group $ G $ acts freely, the equivalence classes can be found from the one-to-one correspondence with the bordisms $ \Omega _ {*} ( B _ {G} ) $ of the classifying space $ B _ {G} $( cf. Bordism).
Recent results (mid-1970s) mostly concern: 1) the determination of types of orbits with various supplementary assumptions concerning the group $ G $ and the manifold $ X $([6]); 2) the classification of group actions; and 3) finding connections between global invariants of the manifold $ X $ and local properties of the group actions of $ G $ in a neighbourhood of fixed points of $ X ^ {G} $. In solving these problems an important part is played by: methods of modern differential topology (e.g. surgery methods); $ K _ {G} $- theory [1], which is the analogue of $ K $- theory for $ G $- vector bundles; bordism and cobordism theories [3]; and analytical methods of studying the action of the group $ G $ based on the study of pseudo-differential operators in $ G $- bundles [2], [7].
References
| [1] | M.F. Atiyah, "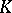 -theory: lectures" , Benjamin (1967) -theory: lectures" , Benjamin (1967) |
| [2] | M.F. Atiyah, I.M. Singer, "The index of elliptic operators" Ann. of Math. (2) , 87 (1968) pp. 484–530 |
| [3] | V.M. Bukhshtaber, A.S. Mishchenko, S.P. Novikov, "Formal groups and their role in the apparatus of algebraic topology" Russian Math. Surveys , 26 (1971) pp. 63–90 Uspekhi Mat. Nauk , 26 : 2 (1971) pp. 131–154 |
| [4] | P.E. Conner, E.E. Floyd, "Differentiable periodic maps" , Springer (1964) |
| [5] | G. Bredon, "Introduction to compact transformation groups" , Acad. Press (1972) |
| [6] | W.Y. Hsiang, "Cohomology theory of topological transformation groups" , Springer (1975) |
| [7] | D.B. Zagier, "Equivariant Pontryagin classes and applications to orbit spaces" , Springer (1972) |
| [8] | , Proc. conf. transformation groups , Springer (1968) |
| [9] | , Proc. 2-nd conf. compact transformation groups , Springer (1972) |
Comments
References
| [a1] | T. Petrie, J.D. Randall, "Transformation groups on manifolds" , M. Dekker (1984) |
Action of a group on a manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Action_of_a_group_on_a_manifold&oldid=45017