Difference between revisions of "Lie algebra, graded"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | l0584301.png | ||
| + | $#A+1 = 204 n = 1 | ||
| + | $#C+1 = 204 : ~/encyclopedia/old_files/data/L058/L.0508430 Lie algebra, graded | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | Graded Lie algebras play an important role in the classification of simple finite-dimensional Lie algebras, Jordan algebras and their generalizations, and primitive pseudo-groups of transformations (see [[#References|[3]]], [[#References|[4]]]). For any semi-simple real Lie algebra its [[Cartan decomposition|Cartan decomposition]] can be regarded as a | + | {{TEX|auto}} |
| + | {{TEX|done}} | ||
| + | |||
| + | A [[Lie algebra|Lie algebra]] $ \mathfrak g $ | ||
| + | over a field $ K $ | ||
| + | that is graded by means of an Abelian group $ A $, | ||
| + | that is, which splits into a direct sum of subspaces $ \mathfrak g _ \alpha $, | ||
| + | $ \alpha \in A $, | ||
| + | in such a way that $ [ \mathfrak g _ \alpha , \mathfrak g _ \beta ] \subseteq \mathfrak g _ {\alpha + \beta } $. | ||
| + | If $ A $ | ||
| + | is an [[Ordered group|ordered group]], then for every filtered Lie algebra (cf. [[Filtered algebra|Filtered algebra]]) the [[Graded algebra|graded algebra]] associated with it is a graded Lie algebra. | ||
| + | |||
| + | Graded Lie algebras play an important role in the classification of simple finite-dimensional Lie algebras, Jordan algebras and their generalizations, and primitive pseudo-groups of transformations (see [[#References|[3]]], [[#References|[4]]]). For any semi-simple real Lie algebra its [[Cartan decomposition|Cartan decomposition]] can be regarded as a $ \mathbf Z _ {2} $- | ||
| + | grading. The local classification of symmetric Riemannian spaces reduces to the classification of $ \mathbf Z _ {2} $- | ||
| + | graded simple complex Lie algebras [[#References|[6]]]. | ||
==Some constructions of graded Lie algebras.== | ==Some constructions of graded Lie algebras.== | ||
| + | 1) Let $ U $ | ||
| + | be an associative algebra (cf. [[Associative rings and algebras|Associative rings and algebras]]) endowed with an increasing filtration $ ( U _ {k} : k \in \mathbf Z ) $, | ||
| + | suppose that $ [ U _ {k} , U _ {l} ] \subset U _ {k+l-d} $, | ||
| + | where $ d $ | ||
| + | is a fixed natural number, and let $ \mathfrak u _ {k} = U _ {k+d} / U _ {k+d-1} $. | ||
| + | Then the commutation operation in $ U $ | ||
| + | induces in the space $ \mathfrak u = \sum _ {k = - \infty } ^ \infty \mathfrak u _ {k} $ | ||
| + | the structure of a $ \mathbf Z $- | ||
| + | graded Lie algebra. In this way one can obtain some Lie algebras of functions with the [[Poisson brackets|Poisson brackets]] as commutator. In the next two examples, $ U _ {k} = U _ {1} ^ {k} $ | ||
| + | for $ k > 0 $ | ||
| + | and $ U _ {k} = 0 $ | ||
| + | for $ k < 0 $. | ||
| − | + | a) Let $ U $ | |
| − | + | be the algebra of linear differential operators with polynomial coefficients and let $ U _ {1} $ | |
| − | + | be the subspace spanned by its generators $ p _ {i} = \partial / {\partial x _ {i} } $, | |
| + | $ q _ {i} = x _ {i} $, | ||
| + | $ i = 1 \dots m $. | ||
| + | Then $ [ U _ {k} , U _ {l} ] \subset U _ {k+l-2} $ | ||
| + | and $ \mathfrak u $ | ||
| + | is the Lie algebra of polynomials in $ p _ {i} $ | ||
| + | and $ q _ {i} $ | ||
| + | with the usual Poisson brackets. | ||
| − | b) Let | + | b) Let $ U $ |
| + | be the [[Universal enveloping algebra|universal enveloping algebra]] of a finite-dimensional Lie algebra $ \mathfrak g $ | ||
| + | and let $ U _ {1} = \mathfrak g $. | ||
| + | Then $ [ U _ {k} , U _ {l} ] \subset U _ {k+l-1} $ | ||
| + | and $ \mathfrak u $ | ||
| + | is canonically isomorphic (as a vector space) to the symmetric algebra over $ \mathfrak g $, | ||
| + | that is, to the algebra of polynomials on the dual space $ \mathfrak g ^ {*} $( | ||
| + | the Poincaré–Birkhoff–Witt theorem). If $ \mathfrak g $ | ||
| + | is the Lie algebra of a connected Lie group $ G $, | ||
| + | then the commutator of elements of $ \mathfrak u $ | ||
| + | can be interpreted either as the Poisson brackets for the corresponding left-invariant functions on the cotangent bundle $ T ^ {*} G $, | ||
| + | or as the Poisson brackets on each orbit of the co-adjoint representation, defined by means of the standard symplectic structure on these orbits. | ||
| − | 2) Suppose that | + | 2) Suppose that $ \mathop{\rm char} k \neq 2 $ |
| + | and that $ E $ | ||
| + | is an $ n $- | ||
| + | dimensional vector space over $ k $ | ||
| + | endowed with a non-singular quadratic form $ Q $; | ||
| + | let $ e _ {1} \dots e _ {n} $ | ||
| + | be an orthogonal basis of $ E $. | ||
| + | The decomposition of the [[Clifford algebra|Clifford algebra]] $ C (Q) $ | ||
| + | into the sum of one-dimensional subspaces $ \langle e _ {i _ {1} } \dots e _ {i _ {k} } \rangle $, | ||
| + | $ i _ {1} < \dots < i _ {k} $, | ||
| + | is a $ \mathbf Z _ {2} ^ {n} $- | ||
| + | grading of it. For $ n = 2m $ | ||
| + | the elements of the algebra $ C (Q) $ | ||
| + | with zero trace form a simple graded Lie algebra of type $ A _ {N} $, | ||
| + | $ N = 2 ^ {m} - 1 $; | ||
| + | its grading has a high degree of symmetry; in particular, all graded subspaces are equivalent. Similar gradings (by means of various finite groups) exist for other simple Lie algebras [[#References|[1]]]. | ||
| − | 3) To every Lie [[Pseudo-group|pseudo-group]] of transformations corresponds a Lie algebra of vector fields. The germ | + | 3) To every Lie [[Pseudo-group|pseudo-group]] of transformations corresponds a Lie algebra of vector fields. The germ $ l $ |
| + | of this Lie algebra at any point has a natural $ \mathbf Z $- | ||
| + | filtration | ||
| − | + | $$ | |
| + | l = l _ {-1} \supset l _ {0} \supset l _ {1} \supset \dots , | ||
| + | $$ | ||
| − | where | + | where $ l _ {k} $ |
| + | contains the germs of those vector fields whose coordinates can be expanded in power series without terms of degree less than $ k + 1 $. | ||
| + | The associated graded Lie algebra can be interpreted as a Lie algebra of polynomial vector fields. | ||
==The classification of simple graded Lie algebras.== | ==The classification of simple graded Lie algebras.== | ||
To simple primitive Lie pseudo-groups correspond the following four series of simple infinite-dimensional graded Lie algebras (see [[#References|[5]]]): | To simple primitive Lie pseudo-groups correspond the following four series of simple infinite-dimensional graded Lie algebras (see [[#References|[5]]]): | ||
| − | + | $ W _ {n} $, | |
| + | the Lie algebra of all polynomial vector fields in the $ n $- | ||
| + | dimensional affine space; | ||
| − | + | $ S _ {n} $, | |
| + | its subalgebra consisting of vector fields with zero divergence; | ||
| − | + | $ H _ {n} $, | |
| + | where $ n = 2 m $, | ||
| + | the subalgebra consisting of vector fields that annihilate the differential form | ||
| − | + | $$ | |
| + | \sum _ { i=1 } ^ { m } | ||
| + | d x _ {i} \wedge d x _ {m+i} $$ | ||
(Hamiltonian vector fields); | (Hamiltonian vector fields); | ||
| − | + | $ K _ {n} $, | |
| + | where $ n = 2 m + 1 $, | ||
| + | the subalgebra consisting of vector fields that multiply the differential form | ||
| − | + | $$ | |
| + | \sum _ { i=1 } ^ { m } | ||
| + | ( x _ {m+i} d x _ {i} - x _ {i} d x _ {m+i} ) + d x _ {n} $$ | ||
by a function. | by a function. | ||
| − | Over fields of characteristic | + | Over fields of characteristic $ p > 0 $ |
| + | one can define simple finite-dimensional graded Lie algebras analogous to $ W _ {n} $, | ||
| + | $ S _ {n} $, | ||
| + | $ H _ {n} $, | ||
| + | and $ K _ {n} $( | ||
| + | see [[#References|[5]]]). | ||
| − | Simple graded Lie algebras of another type are obtained in the following way [[#References|[4]]]. Let | + | Simple graded Lie algebras of another type are obtained in the following way [[#References|[4]]]. Let $ \mathfrak g = \mathfrak g (A) $ |
| + | be the Lie algebra defined by means of an indecomposable Cartan matrix $ A = \| a _ {ij} \| $, | ||
| + | $ i , j = 1 \dots n $( | ||
| + | from now on the notation of the article [[Cartan matrix|Cartan matrix]] is used). The algebra $ \mathfrak g $ | ||
| + | is endowed with a $ \mathbf Z ^ {k} $- | ||
| + | grading so that $ h _ {i} \in \mathfrak g _ {0} $, | ||
| + | $ e _ {i} \in \mathfrak g _ {\alpha _ {i} } $, | ||
| + | $ f _ {i} \in \mathfrak g _ {- \alpha _ {i} } $, | ||
| + | where $ \alpha _ {i} $ | ||
| + | is the row $ ( 0 \dots 1 \dots 0 ) $ | ||
| + | with $ 1 $ | ||
| + | in the $ i $- | ||
| + | th place. Elements $ \alpha \in \mathbf Z ^ {n} $ | ||
| + | for which $ \mathfrak g _ \alpha \neq 0 $ | ||
| + | are called roots, and the $ \alpha _ {i} $ | ||
| + | are called simple roots. Any root is a linear combination of simple roots with integer coefficients of the same sign and $ \mathop{\rm dim} \mathfrak g _ \alpha < \infty $ | ||
| + | for any $ \alpha \in \mathbf Z ^ {n} $. | ||
| + | The quotient algebra $ {\mathfrak g } ^ \prime (A) $ | ||
| + | of $ \mathfrak g $ | ||
| + | with respect to its centre, which lies in $ \mathfrak g _ {0} $, | ||
| + | is simple as a graded algebra, that is, it does not have non-trivial graded ideals. | ||
| − | Let | + | Let $ R $ |
| + | be the totality of linear combinations of rows of the matrix $ A $ | ||
| + | with positive coefficients. Then one of the following cases holds: | ||
| − | (P) | + | (P) $ R $ |
| + | contains a row all elements of which are positive; | ||
| − | (Z) | + | (Z) $ R $ |
| + | contains a zero row; | ||
| − | (N) | + | (N) $ R $ |
| + | contains a row all elements of which are negative. | ||
| − | In the case (P), | + | In the case (P), $ \mathfrak g (A) = \mathfrak g ^ \prime (A) $ |
| + | is a simple finite-dimensional Lie algebra. In the case (N), $ \mathfrak g (A) $ | ||
| + | is a simple infinite-dimensional Lie algebra. In the case (Z), the algebra $ \mathfrak g ^ \prime = \mathfrak g ^ \prime (A) $ | ||
| + | is simple only as a graded algebra. It can be converted in a $ K [ u , u ^ {-1} ] $- | ||
| + | algebra so that: a) $ u \mathfrak g _ \alpha ^ \prime = \mathfrak g _ {\alpha + \nu } ^ \prime $, | ||
| + | where $ \nu $ | ||
| + | is a row of positive numbers; and b) the quotient algebra $ \mathfrak g ^ \prime / ( 1 - u ) \mathfrak g ^ \prime = \overline{ {\mathfrak g }}\; $ | ||
| + | is a simple finite-dimensional Lie algebra. The greatest common divisor of all components $ \nu _ {i} $ | ||
| + | of the row $ \nu $, | ||
| + | which is equal to 1, 2 or 3, is called the index of the algebra $ \mathfrak g ^ \prime $. | ||
| − | The following table is a list of all simple graded Lie algebras with Cartan matrix of type (Z). Here the algebra | + | The following table is a list of all simple graded Lie algebras with Cartan matrix of type (Z). Here the algebra $ \mathfrak g ^ \prime $ |
| + | is denoted by the same symbol as the associated simple finite-dimensional Lie algebra $ \overline{ {\mathfrak g }}\; $, | ||
| + | but with the addition of its index, given in brackets. | ||
| − | The diagram of simple roots describes the matrix | + | The diagram of simple roots describes the matrix $ A $. |
| + | Its vertices correspond to the simple roots; the $ i $- | ||
| + | th and $ j $- | ||
| + | th vertices are joined by an $ ( a _ {ij} a _ {ji} ) $- | ||
| + | multiple edge, directed from the $ i $- | ||
| + | th vertex to the $ j $- | ||
| + | th if $ | a _ {ij} | > | a _ {ji} | $, | ||
| + | and undirected if $ | a _ {ij} | = | a _ {ji} | $. | ||
| + | Above the vertices stand the numbers $ \nu _ {i} $. | ||
| + | <table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1">Notation</td> <td colname="2" style="background-color:white;" colspan="1">Diagram of simple roots</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ A _ {n-1} ^ {(1)} $, | ||
| + | $ n \geq 3 $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ A _ {1} ^ {(1)} $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ A _ {2n-2} ^ {(2)} $, |
| + | $ n \geq 3 $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ A _ {2} ^ {(2)} $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ A _ {2n-3} ^ {(2)} $, |
| + | $ n \geq 4 $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ B _ {n-1} ^ {(1)} $, |
| + | $ n \geq 4 $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ C _ {n-1} ^ {(1)} $, |
| + | $ n \geq 3 $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ D _ {n-1} ^ {(1)} $, |
| + | $ n \geq 5 $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ D _ {n} ^ {(2)} $, |
| + | $ n \geq 3 $ | ||
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ D _ {4} ^ {(3)} $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ E _ {6} ^ {(1)} $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ E _ {6} ^ {(2)} $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ E _ {7} ^ {(1)} $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ E _ {8} ^ {(1)} $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ F _ {4} ^ {(1)} $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| − | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> | + | </td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"> $ G _ {2} ^ {(1)} $ |
| + | </td> <td colname="2" style="background-color:white;" colspan="1"> | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/" /> | ||
| Line 123: | Line 279: | ||
</td></tr> </table> | </td></tr> </table> | ||
| − | By means of graded Lie algebras with Cartan matrix of type (Z) one can classify | + | By means of graded Lie algebras with Cartan matrix of type (Z) one can classify $ \mathbf Z _ {m} $- |
| + | graded simple finite-dimensional Lie algebras (see [[#References|[4]]], [[#References|[2]]]). Namely, let $ \mathfrak g ^ \prime = \mathfrak g ^ \prime (A) $, | ||
| + | where $ A $ | ||
| + | satisfies condition (Z), and let $ p : \mathbf Z ^ {n} \rightarrow \mathbf Z $ | ||
| + | be a homomorphism such that $ p ( \alpha _ {i} ) \geq 0 $ | ||
| + | and $ p ( \nu ) = m $. | ||
| + | Then $ \mathfrak g _ {k} ^ \prime = \sum _ {p ( \alpha ) = k } \mathfrak g _ \alpha ^ \prime $ | ||
| + | for any $ k \in \mathbf Z $ | ||
| + | is mapped isomorphically onto the subspace $ \overline{ {\mathfrak g }}\; _ {k} \subset \overline{ {\mathfrak g }}\; $, | ||
| + | which depends only on the residue of $ k $ | ||
| + | modulo $ m $, | ||
| + | and the decomposition $ \overline{ {\mathfrak g }}\; = \sum _ {k=0} ^ {m-1} \overline{ {\mathfrak g }}\; _ {k} $ | ||
| + | is a $ \mathbf Z _ {m} $- | ||
| + | grading of $ \overline{ {\mathfrak g }}\; $. | ||
| + | If the field $ K $ | ||
| + | is algebraically closed, then by the method described one obtains, without repetition, all $ \mathbf Z _ {m} $- | ||
| + | graded simple finite-dimensional Lie algebras over $ K $. | ||
| + | The index of $ \mathfrak g ^ \prime $ | ||
| + | is equal to the order of the automorphism $ \theta : x \mapsto ( \mathop{\rm exp} ( {2 \pi i k } / m )) x $, | ||
| + | $ x \in \mathfrak g _ {k} $, | ||
| + | of the algebra $ \overline{ {\mathfrak g }}\; $ | ||
| + | modulo the group of inner automorphisms. | ||
| − | There is a classification of simple | + | There is a classification of simple $ \mathbf Z $- |
| + | graded Lie algebras $ \mathfrak g = \sum _ {k = - \infty } ^ \infty \mathfrak g _ {k} $ | ||
| + | satisfying the conditions: a) $ \mathop{\rm dim} \mathfrak g _ {k} \leq C | k | ^ {N} $ | ||
| + | for some $ C $ | ||
| + | and $ N $; | ||
| + | b) $ \mathfrak g $ | ||
| + | is generated by the subspace $ \mathfrak g _ {-1} + \mathfrak g _ {0} + \mathfrak g _ {1} $; | ||
| + | and c) the representation of $ \mathfrak g _ {0} $ | ||
| + | on $ \mathfrak g _ {-1} $ | ||
| + | is irreducible. In this case either $ \mathfrak g $ | ||
| + | is finite-dimensional or it is one of the algebras $ W _ {n} $, | ||
| + | $ S _ {n} $, | ||
| + | $ H _ {n} $, | ||
| + | $ K _ {n} $, | ||
| + | or it is the algebra $ \mathfrak g ^ \prime (A) $ | ||
| + | defined by a Cartan matrix of type (Z), endowed with a suitable $ \mathbf Z $- | ||
| + | grading [[#References|[4]]]. | ||
| − | A Lie [[Superalgebra|superalgebra]] is sometimes called a | + | A Lie [[Superalgebra|superalgebra]] is sometimes called a $ \mathbf Z _ {2} $- |
| + | graded Lie algebra. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.V. Alekseevskii, "Finite commutative Jordan subgroups of complex simple Lie groups" ''Funct. Anal. Appl.'' , '''8''' : 4 (1974) pp. 277–279 ''Funktsional. Anal. Prilozhen.'' , '''8''' : 4 (1974) pp. 1–4</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E.B. Vinberg, "The Weyl group of a graded Lie algebra" ''Math. USSR Izv.'' , '''10''' (1976) pp. 436–496 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''40''' : 3 (1976) pp. 488–526</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.L. Kantor, "Certain generalizations of Jordan algebras" ''Trudy Sem. Vektor. Tenzor. Anal.'' , '''16''' (1972) pp. 407–499 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.G. Kac, "Simple irreducible graded Lie algebras of finite growth" ''Math. USSR Izv.'' , '''2''' (1968) pp. 1271–1312 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''32''' : 6 (1968) pp. 1323–1367</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> A.I. Kostrikin, I.R. Shafarevich, "Graded Lie algebras of finite characteristic" ''Math. USSR Izv.'' , '''3''' (1969) pp. 237–304 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''33''' : 2 (1969) pp. 252–322</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.V. Alekseevskii, "Finite commutative Jordan subgroups of complex simple Lie groups" ''Funct. Anal. Appl.'' , '''8''' : 4 (1974) pp. 277–279 ''Funktsional. Anal. Prilozhen.'' , '''8''' : 4 (1974) pp. 1–4</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> E.B. Vinberg, "The Weyl group of a graded Lie algebra" ''Math. USSR Izv.'' , '''10''' (1976) pp. 436–496 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''40''' : 3 (1976) pp. 488–526</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.L. Kantor, "Certain generalizations of Jordan algebras" ''Trudy Sem. Vektor. Tenzor. Anal.'' , '''16''' (1972) pp. 407–499 (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.G. Kac, "Simple irreducible graded Lie algebras of finite growth" ''Math. USSR Izv.'' , '''2''' (1968) pp. 1271–1312 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''32''' : 6 (1968) pp. 1323–1367</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> A.I. Kostrikin, I.R. Shafarevich, "Graded Lie algebras of finite characteristic" ''Math. USSR Izv.'' , '''3''' (1969) pp. 237–304 ''Izv. Akad. Nauk SSSR Ser. Mat.'' , '''33''' : 2 (1969) pp. 252–322</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978)</TD></TR></table> | ||
| + | ====Comments==== | ||
| + | The Lie algebras $ \mathfrak g (A) $ | ||
| + | are called Kac–Moody algebras; they have close connections with many areas of mathematics and mathematical physics (cf. [[#References|[a2]]]). | ||
| + | There is a second notion which also sometimes goes by the name of graded Lie algebra. This is a $ \mathbf Z $- | ||
| + | or $ \mathbf Z / (2) $- | ||
| + | graded vector space $ V = \oplus V _ {i} $ | ||
| + | with a multiplication | ||
| − | + | $$ | |
| − | + | [ , ] : V \times V \rightarrow V | |
| + | $$ | ||
| − | + | such that | |
| − | + | $$ | |
| + | [ V _ {i} , V _ {j} ] \subset V _ {i+j} , | ||
| + | $$ | ||
| − | + | $$ | |
| + | [ x , y ] = ( - 1 ) ^ {ij+1} [ y , x ] , | ||
| + | $$ | ||
| − | + | for all $ x \in V _ {i} $, | |
| + | $ y \in V _ {j} $, | ||
| + | and | ||
| − | + | $$ | |
| + | ( - 1 ) ^ {ik} | ||
| + | [ [ x , y ] , z ] + ( - 1 ) ^ {ji} [ [ y , z ] , x ] + | ||
| + | ( - 1 ) ^ {kj} [ [ z , x ] , y ] = 0 , | ||
| + | $$ | ||
| − | for all | + | for all $ x \in V _ {i} $, |
| + | $ y \in V _ {j} $, | ||
| + | $ z \in V _ {k} $. | ||
| + | One also says that $ V = \oplus V _ {i} $ | ||
| + | has been equipped with a graded Lie product or graded Lie bracket. | ||
| − | + | Graded Lie brackets naturally arise, for instance, in cohomology theory in the context of deformations of algebras and complex structures, [[#References|[a4]]]. A graded vector space $ V $ | |
| + | with a graded Lie bracket is not a Lie algebra in the usual sense of the word. A Lie superalgebra is a $ \mathbf Z / (2) $- | ||
| + | graded vector space with a $ \mathbf Z / (2) $- | ||
| + | graded Lie bracket. | ||
| − | + | Of fundamental importance in recent progress in quantum field theory is the Virasoro algebra. This is a ( $ \mathbf Z $- | |
| + | graded) Lie algebra with a basis $ L _ {k} $( | ||
| + | $ k \in \mathbf Z $) | ||
| + | and $ c $, | ||
| + | and the following commutation relations: | ||
| − | + | $$ | |
| + | [ L _ {m} , L _ {n} ] = \ | ||
| + | ( m - n ) L _ {m+n} + | ||
| − | + | \frac{m ^ {3} - m }{12} | |
| − | + | \delta _ {m , - n } c . | |
| + | $$ | ||
See [[#References|[a1]]]. | See [[#References|[a1]]]. | ||
Revision as of 16:40, 31 March 2020
A Lie algebra $ \mathfrak g $
over a field $ K $
that is graded by means of an Abelian group $ A $,
that is, which splits into a direct sum of subspaces $ \mathfrak g _ \alpha $,
$ \alpha \in A $,
in such a way that $ [ \mathfrak g _ \alpha , \mathfrak g _ \beta ] \subseteq \mathfrak g _ {\alpha + \beta } $.
If $ A $
is an ordered group, then for every filtered Lie algebra (cf. Filtered algebra) the graded algebra associated with it is a graded Lie algebra.
Graded Lie algebras play an important role in the classification of simple finite-dimensional Lie algebras, Jordan algebras and their generalizations, and primitive pseudo-groups of transformations (see [3], [4]). For any semi-simple real Lie algebra its Cartan decomposition can be regarded as a $ \mathbf Z _ {2} $- grading. The local classification of symmetric Riemannian spaces reduces to the classification of $ \mathbf Z _ {2} $- graded simple complex Lie algebras [6].
Some constructions of graded Lie algebras.
1) Let $ U $ be an associative algebra (cf. Associative rings and algebras) endowed with an increasing filtration $ ( U _ {k} : k \in \mathbf Z ) $, suppose that $ [ U _ {k} , U _ {l} ] \subset U _ {k+l-d} $, where $ d $ is a fixed natural number, and let $ \mathfrak u _ {k} = U _ {k+d} / U _ {k+d-1} $. Then the commutation operation in $ U $ induces in the space $ \mathfrak u = \sum _ {k = - \infty } ^ \infty \mathfrak u _ {k} $ the structure of a $ \mathbf Z $- graded Lie algebra. In this way one can obtain some Lie algebras of functions with the Poisson brackets as commutator. In the next two examples, $ U _ {k} = U _ {1} ^ {k} $ for $ k > 0 $ and $ U _ {k} = 0 $ for $ k < 0 $.
a) Let $ U $ be the algebra of linear differential operators with polynomial coefficients and let $ U _ {1} $ be the subspace spanned by its generators $ p _ {i} = \partial / {\partial x _ {i} } $, $ q _ {i} = x _ {i} $, $ i = 1 \dots m $. Then $ [ U _ {k} , U _ {l} ] \subset U _ {k+l-2} $ and $ \mathfrak u $ is the Lie algebra of polynomials in $ p _ {i} $ and $ q _ {i} $ with the usual Poisson brackets.
b) Let $ U $ be the universal enveloping algebra of a finite-dimensional Lie algebra $ \mathfrak g $ and let $ U _ {1} = \mathfrak g $. Then $ [ U _ {k} , U _ {l} ] \subset U _ {k+l-1} $ and $ \mathfrak u $ is canonically isomorphic (as a vector space) to the symmetric algebra over $ \mathfrak g $, that is, to the algebra of polynomials on the dual space $ \mathfrak g ^ {*} $( the Poincaré–Birkhoff–Witt theorem). If $ \mathfrak g $ is the Lie algebra of a connected Lie group $ G $, then the commutator of elements of $ \mathfrak u $ can be interpreted either as the Poisson brackets for the corresponding left-invariant functions on the cotangent bundle $ T ^ {*} G $, or as the Poisson brackets on each orbit of the co-adjoint representation, defined by means of the standard symplectic structure on these orbits.
2) Suppose that $ \mathop{\rm char} k \neq 2 $ and that $ E $ is an $ n $- dimensional vector space over $ k $ endowed with a non-singular quadratic form $ Q $; let $ e _ {1} \dots e _ {n} $ be an orthogonal basis of $ E $. The decomposition of the Clifford algebra $ C (Q) $ into the sum of one-dimensional subspaces $ \langle e _ {i _ {1} } \dots e _ {i _ {k} } \rangle $, $ i _ {1} < \dots < i _ {k} $, is a $ \mathbf Z _ {2} ^ {n} $- grading of it. For $ n = 2m $ the elements of the algebra $ C (Q) $ with zero trace form a simple graded Lie algebra of type $ A _ {N} $, $ N = 2 ^ {m} - 1 $; its grading has a high degree of symmetry; in particular, all graded subspaces are equivalent. Similar gradings (by means of various finite groups) exist for other simple Lie algebras [1].
3) To every Lie pseudo-group of transformations corresponds a Lie algebra of vector fields. The germ $ l $ of this Lie algebra at any point has a natural $ \mathbf Z $- filtration
$$ l = l _ {-1} \supset l _ {0} \supset l _ {1} \supset \dots , $$
where $ l _ {k} $ contains the germs of those vector fields whose coordinates can be expanded in power series without terms of degree less than $ k + 1 $. The associated graded Lie algebra can be interpreted as a Lie algebra of polynomial vector fields.
The classification of simple graded Lie algebras.
To simple primitive Lie pseudo-groups correspond the following four series of simple infinite-dimensional graded Lie algebras (see [5]):
$ W _ {n} $, the Lie algebra of all polynomial vector fields in the $ n $- dimensional affine space;
$ S _ {n} $, its subalgebra consisting of vector fields with zero divergence;
$ H _ {n} $, where $ n = 2 m $, the subalgebra consisting of vector fields that annihilate the differential form
$$ \sum _ { i=1 } ^ { m } d x _ {i} \wedge d x _ {m+i} $$
(Hamiltonian vector fields);
$ K _ {n} $, where $ n = 2 m + 1 $, the subalgebra consisting of vector fields that multiply the differential form
$$ \sum _ { i=1 } ^ { m } ( x _ {m+i} d x _ {i} - x _ {i} d x _ {m+i} ) + d x _ {n} $$
by a function.
Over fields of characteristic $ p > 0 $ one can define simple finite-dimensional graded Lie algebras analogous to $ W _ {n} $, $ S _ {n} $, $ H _ {n} $, and $ K _ {n} $( see [5]).
Simple graded Lie algebras of another type are obtained in the following way [4]. Let $ \mathfrak g = \mathfrak g (A) $ be the Lie algebra defined by means of an indecomposable Cartan matrix $ A = \| a _ {ij} \| $, $ i , j = 1 \dots n $( from now on the notation of the article Cartan matrix is used). The algebra $ \mathfrak g $ is endowed with a $ \mathbf Z ^ {k} $- grading so that $ h _ {i} \in \mathfrak g _ {0} $, $ e _ {i} \in \mathfrak g _ {\alpha _ {i} } $, $ f _ {i} \in \mathfrak g _ {- \alpha _ {i} } $, where $ \alpha _ {i} $ is the row $ ( 0 \dots 1 \dots 0 ) $ with $ 1 $ in the $ i $- th place. Elements $ \alpha \in \mathbf Z ^ {n} $ for which $ \mathfrak g _ \alpha \neq 0 $ are called roots, and the $ \alpha _ {i} $ are called simple roots. Any root is a linear combination of simple roots with integer coefficients of the same sign and $ \mathop{\rm dim} \mathfrak g _ \alpha < \infty $ for any $ \alpha \in \mathbf Z ^ {n} $. The quotient algebra $ {\mathfrak g } ^ \prime (A) $ of $ \mathfrak g $ with respect to its centre, which lies in $ \mathfrak g _ {0} $, is simple as a graded algebra, that is, it does not have non-trivial graded ideals.
Let $ R $ be the totality of linear combinations of rows of the matrix $ A $ with positive coefficients. Then one of the following cases holds:
(P) $ R $ contains a row all elements of which are positive;
(Z) $ R $ contains a zero row;
(N) $ R $ contains a row all elements of which are negative.
In the case (P), $ \mathfrak g (A) = \mathfrak g ^ \prime (A) $ is a simple finite-dimensional Lie algebra. In the case (N), $ \mathfrak g (A) $ is a simple infinite-dimensional Lie algebra. In the case (Z), the algebra $ \mathfrak g ^ \prime = \mathfrak g ^ \prime (A) $ is simple only as a graded algebra. It can be converted in a $ K [ u , u ^ {-1} ] $- algebra so that: a) $ u \mathfrak g _ \alpha ^ \prime = \mathfrak g _ {\alpha + \nu } ^ \prime $, where $ \nu $ is a row of positive numbers; and b) the quotient algebra $ \mathfrak g ^ \prime / ( 1 - u ) \mathfrak g ^ \prime = \overline{ {\mathfrak g }}\; $ is a simple finite-dimensional Lie algebra. The greatest common divisor of all components $ \nu _ {i} $ of the row $ \nu $, which is equal to 1, 2 or 3, is called the index of the algebra $ \mathfrak g ^ \prime $.
The following table is a list of all simple graded Lie algebras with Cartan matrix of type (Z). Here the algebra $ \mathfrak g ^ \prime $ is denoted by the same symbol as the associated simple finite-dimensional Lie algebra $ \overline{ {\mathfrak g }}\; $, but with the addition of its index, given in brackets.
The diagram of simple roots describes the matrix $ A $. Its vertices correspond to the simple roots; the $ i $- th and $ j $- th vertices are joined by an $ ( a _ {ij} a _ {ji} ) $- multiple edge, directed from the $ i $- th vertex to the $ j $- th if $ | a _ {ij} | > | a _ {ji} | $, and undirected if $ | a _ {ij} | = | a _ {ji} | $. Above the vertices stand the numbers $ \nu _ {i} $.
<tbody> </tbody>
|
By means of graded Lie algebras with Cartan matrix of type (Z) one can classify $ \mathbf Z _ {m} $- graded simple finite-dimensional Lie algebras (see [4], [2]). Namely, let $ \mathfrak g ^ \prime = \mathfrak g ^ \prime (A) $, where $ A $ satisfies condition (Z), and let $ p : \mathbf Z ^ {n} \rightarrow \mathbf Z $ be a homomorphism such that $ p ( \alpha _ {i} ) \geq 0 $ and $ p ( \nu ) = m $. Then $ \mathfrak g _ {k} ^ \prime = \sum _ {p ( \alpha ) = k } \mathfrak g _ \alpha ^ \prime $ for any $ k \in \mathbf Z $ is mapped isomorphically onto the subspace $ \overline{ {\mathfrak g }}\; _ {k} \subset \overline{ {\mathfrak g }}\; $, which depends only on the residue of $ k $ modulo $ m $, and the decomposition $ \overline{ {\mathfrak g }}\; = \sum _ {k=0} ^ {m-1} \overline{ {\mathfrak g }}\; _ {k} $ is a $ \mathbf Z _ {m} $- grading of $ \overline{ {\mathfrak g }}\; $. If the field $ K $ is algebraically closed, then by the method described one obtains, without repetition, all $ \mathbf Z _ {m} $- graded simple finite-dimensional Lie algebras over $ K $. The index of $ \mathfrak g ^ \prime $ is equal to the order of the automorphism $ \theta : x \mapsto ( \mathop{\rm exp} ( {2 \pi i k } / m )) x $, $ x \in \mathfrak g _ {k} $, of the algebra $ \overline{ {\mathfrak g }}\; $ modulo the group of inner automorphisms.
There is a classification of simple $ \mathbf Z $- graded Lie algebras $ \mathfrak g = \sum _ {k = - \infty } ^ \infty \mathfrak g _ {k} $ satisfying the conditions: a) $ \mathop{\rm dim} \mathfrak g _ {k} \leq C | k | ^ {N} $ for some $ C $ and $ N $; b) $ \mathfrak g $ is generated by the subspace $ \mathfrak g _ {-1} + \mathfrak g _ {0} + \mathfrak g _ {1} $; and c) the representation of $ \mathfrak g _ {0} $ on $ \mathfrak g _ {-1} $ is irreducible. In this case either $ \mathfrak g $ is finite-dimensional or it is one of the algebras $ W _ {n} $, $ S _ {n} $, $ H _ {n} $, $ K _ {n} $, or it is the algebra $ \mathfrak g ^ \prime (A) $ defined by a Cartan matrix of type (Z), endowed with a suitable $ \mathbf Z $- grading [4].
A Lie superalgebra is sometimes called a $ \mathbf Z _ {2} $- graded Lie algebra.
References
| [1] | A.V. Alekseevskii, "Finite commutative Jordan subgroups of complex simple Lie groups" Funct. Anal. Appl. , 8 : 4 (1974) pp. 277–279 Funktsional. Anal. Prilozhen. , 8 : 4 (1974) pp. 1–4 |
| [2] | E.B. Vinberg, "The Weyl group of a graded Lie algebra" Math. USSR Izv. , 10 (1976) pp. 436–496 Izv. Akad. Nauk SSSR Ser. Mat. , 40 : 3 (1976) pp. 488–526 |
| [3] | I.L. Kantor, "Certain generalizations of Jordan algebras" Trudy Sem. Vektor. Tenzor. Anal. , 16 (1972) pp. 407–499 (In Russian) |
| [4] | V.G. Kac, "Simple irreducible graded Lie algebras of finite growth" Math. USSR Izv. , 2 (1968) pp. 1271–1312 Izv. Akad. Nauk SSSR Ser. Mat. , 32 : 6 (1968) pp. 1323–1367 |
| [5] | A.I. Kostrikin, I.R. Shafarevich, "Graded Lie algebras of finite characteristic" Math. USSR Izv. , 3 (1969) pp. 237–304 Izv. Akad. Nauk SSSR Ser. Mat. , 33 : 2 (1969) pp. 252–322 |
| [6] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) |
Comments
The Lie algebras $ \mathfrak g (A) $ are called Kac–Moody algebras; they have close connections with many areas of mathematics and mathematical physics (cf. [a2]).
There is a second notion which also sometimes goes by the name of graded Lie algebra. This is a $ \mathbf Z $- or $ \mathbf Z / (2) $- graded vector space $ V = \oplus V _ {i} $ with a multiplication
$$ [ , ] : V \times V \rightarrow V $$
such that
$$ [ V _ {i} , V _ {j} ] \subset V _ {i+j} , $$
$$ [ x , y ] = ( - 1 ) ^ {ij+1} [ y , x ] , $$
for all $ x \in V _ {i} $, $ y \in V _ {j} $, and
$$ ( - 1 ) ^ {ik} [ [ x , y ] , z ] + ( - 1 ) ^ {ji} [ [ y , z ] , x ] + ( - 1 ) ^ {kj} [ [ z , x ] , y ] = 0 , $$
for all $ x \in V _ {i} $, $ y \in V _ {j} $, $ z \in V _ {k} $. One also says that $ V = \oplus V _ {i} $ has been equipped with a graded Lie product or graded Lie bracket.
Graded Lie brackets naturally arise, for instance, in cohomology theory in the context of deformations of algebras and complex structures, [a4]. A graded vector space $ V $ with a graded Lie bracket is not a Lie algebra in the usual sense of the word. A Lie superalgebra is a $ \mathbf Z / (2) $- graded vector space with a $ \mathbf Z / (2) $- graded Lie bracket.
Of fundamental importance in recent progress in quantum field theory is the Virasoro algebra. This is a ( $ \mathbf Z $- graded) Lie algebra with a basis $ L _ {k} $( $ k \in \mathbf Z $) and $ c $, and the following commutation relations:
$$ [ L _ {m} , L _ {n} ] = \ ( m - n ) L _ {m+n} + \frac{m ^ {3} - m }{12} \delta _ {m , - n } c . $$
See [a1].
References
| [a1] | V.G. Kac, A.K. Raina, "Bombay lectures on highest weight representations" , World Sci. (1987) |
| [a2] | V.G. Kac, "Infinite-dimensional Lie algebras" , Cambridge Univ. Press (1985) |
| [a3] | O. Mathieu, "Classification des algèbres de Lie graduées simples de croissance 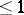 " Invent. Math. , 86 (1986) pp. 371–426 " Invent. Math. , 86 (1986) pp. 371–426 |
| [a4] | M. Hazewinkel (ed.) M. Gerstenhaber (ed.) , Deformation theory of algebras and structures and applications , Kluwer (1988) |
Lie algebra, graded. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_algebra,_graded&oldid=44947