Difference between revisions of "Character formula"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| + | <!-- | ||
| + | c0215201.png | ||
| + | $#A+1 = 26 n = 1 | ||
| + | $#C+1 = 26 : ~/encyclopedia/old_files/data/C021/C.0201520 Character formula, | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
''Weyl formula'' | ''Weyl formula'' | ||
| − | A formula that expresses the character | + | A formula that expresses the character $ \mathop{\rm ch} V ( \Lambda ) $ |
| + | of an irreducible finite-dimensional representation of a semi-simple Lie algebra $ \mathfrak g $ | ||
| + | over an algebraically closed field of characteristic 0 (cf. [[Character of a finite-dimensional representation of a semi-simple Lie algebra|Character of a finite-dimensional representation of a semi-simple Lie algebra]]) in terms of its highest weight $ \Lambda $: | ||
| + | |||
| + | $$ | ||
| + | \mathop{\rm ch} V ( \Lambda ) = \ | ||
| + | |||
| + | \frac{\sum _ {w \in W } | ||
| + | ( \mathop{\rm det} w) e ^ {w ( \Lambda + \rho ) } }{\sum _ {w \in W } | ||
| + | ( \mathop{\rm det} w) e ^ {w ( \rho ) } } | ||
| + | = | ||
| + | $$ | ||
| − | + | $$ | |
| + | = \ | ||
| − | + | \frac{\sum _ {w \in W } ( \mathop{\rm det} w) e ^ {w ( \Lambda + \rho ) - \rho | |
| + | } }{\prod _ {\alpha \in \mathbf R ^ {+} } (1 - e ^ {- \alpha } ) } | ||
| − | + | $$ | |
| − | + | (here $ W $ | |
| + | is the [[Weyl group|Weyl group]] and $ \rho = ( \sum _ {\alpha \in \mathbf R ^ {+} } \alpha )/2 $ | ||
| + | is half the sum of the positive roots of the Lie algebra $ \mathfrak g $). | ||
| + | Consequences of the character formula are the formula for the dimension of the representation: | ||
| − | + | $$ | |
| + | \mathop{\rm dim} V ( \Lambda ) = \ | ||
| + | \prod _ {\alpha \in \mathbf R ^ {+} } | ||
| − | + | \frac{( \Lambda + \rho , \alpha ) }{( \rho , \alpha ) } | |
| + | , | ||
| + | $$ | ||
| − | where | + | a formula for the multiplicity of a weight, and also Steinberg's formula for the number $ m _ \Lambda $ |
| + | of occurrences of the irreducible $ \mathfrak g $- | ||
| + | module $ V ( \Lambda ) $ | ||
| + | in $ V ( \Lambda ^ \prime ) \otimes V ( \Lambda ^ {\prime\prime} ) $: | ||
| + | |||
| + | $$ | ||
| + | m _ \Lambda = \ | ||
| + | \sum _ {s, t \in W } | ||
| + | \mathop{\rm det} (st) | ||
| + | P ( \Lambda + 2 \rho - | ||
| + | s ( \Lambda ^ \prime + \rho ) - | ||
| + | t ( \Lambda ^ {\prime\prime} + \rho )), | ||
| + | $$ | ||
| + | |||
| + | where $ P ( \mu ) $ | ||
| + | is the number of distinct presentations of an element $ \mu $ | ||
| + | as a sum of positive roots (see [[#References|[1]]]). | ||
The character formula can be generalized to the case of irreducible representations of graded Lie algebras defined by an indecomposable [[Cartan matrix|Cartan matrix]] (see also [[Lie algebra, graded|Lie algebra, graded]]). This generalization leads to the following combinatorial identities: | The character formula can be generalized to the case of irreducible representations of graded Lie algebras defined by an indecomposable [[Cartan matrix|Cartan matrix]] (see also [[Lie algebra, graded|Lie algebra, graded]]). This generalization leads to the following combinatorial identities: | ||
| − | + | $$ | |
| + | e (t) = \ | ||
| + | \sum _ {j \in \mathbf Z } | ||
| + | (-1) ^ {j} t ^ {j (3j + 1)/2 } | ||
| + | $$ | ||
(Euler's identity); | (Euler's identity); | ||
| − | + | $$ | |
| + | |||
| + | \frac{e ^ {2} (t) }{e (t ^ {2} ) } | ||
| + | = \ | ||
| + | \sum _ {j \in \mathbf Z } | ||
| + | (-1) ^ {j} t ^ {j ^ {2} } | ||
| + | $$ | ||
(Gauss' identity); | (Gauss' identity); | ||
| − | + | $$ | |
| + | e ^ {3} (t) = \ | ||
| + | \sum _ {j \geq 0 } | ||
| + | (-1) ^ {j} (2j + 1) ^ {j (j + 1)/2 } | ||
| + | $$ | ||
(Jacobi's identity); where | (Jacobi's identity); where | ||
| − | + | $$ | |
| + | e (t) = \ | ||
| + | \prod _ {n \geq 1 } | ||
| + | (1 - t ^ {n} ); | ||
| + | $$ | ||
| − | + | $$ | |
| + | \prod _ {j \geq 1 } (1 - t ^ {5j - 4 } ) ^ {-1} (1 | ||
| + | - t ^ {5j - 1 } ) ^ {-1} = \sum _ {n \geq 0 } | ||
| + | \frac{t ^ {n ^ {2} } }{(1 - t) \dots (1 - t ^ {n} ) } | ||
| + | |||
| + | $$ | ||
(the Rogers–Ramanujan identity); and others (see [[#References|[3]]], [[#References|[4]]]). | (the Rogers–Ramanujan identity); and others (see [[#References|[3]]], [[#References|[4]]]). | ||
| Line 42: | Line 113: | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D.A. Leites, "Formulas for the characters of irreducible finite-dimensional representations of simple Lie superalgebras" ''Funct. Anal. and Appl.'' , '''14''' (1980) pp. 106–109 ''Funktsional. Anal. i Prilozhen.'' , '''14''' : 2 (1980) pp. 35–38</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.G. Kac, "Infinite-dimensional algebras, Dedekind's <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021520/c02152022.png" />-function, classical Möbius function and the very strange formula" ''Adv. in Math.'' , '''30''' : 2 (1978) pp. 85–136</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J. Lepowsky, "Lie algebras and related topics" , Springer (1982)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D.A. Leites, "Formulas for the characters of irreducible finite-dimensional representations of simple Lie superalgebras" ''Funct. Anal. and Appl.'' , '''14''' (1980) pp. 106–109 ''Funktsional. Anal. i Prilozhen.'' , '''14''' : 2 (1980) pp. 35–38</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.G. Kac, "Infinite-dimensional algebras, Dedekind's <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c021/c021520/c02152022.png" />-function, classical Möbius function and the very strange formula" ''Adv. in Math.'' , '''30''' : 2 (1978) pp. 85–136</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> J. Lepowsky, "Lie algebras and related topics" , Springer (1982)</TD></TR></table> | ||
| + | ====Comments==== | ||
| + | The denominator in the Weyl character formula can be written in two different ways: one as a sum, and the other as a product. This identity is called the Weyl denominator formula. It was I.G. Macdonald [[#References|[a1]]] who proved that the denominator formula had a suitable generalization to the case of affine root systems. For the affine root system of type $ A _ {1} ^ {(1)} $, | ||
| + | the formula of Macdonald comes down to the Jacobi triple product identity. Shortly afterwards it was V.G. Kac [[#References|[a2]]] who realized that the Weyl character formula could be generalized to the case of so-called Kac–Moody algebras (cf. also [[Kac–Moody algebra|Kac–Moody algebra]]) with a symmetrizable generalized [[Cartan matrix|Cartan matrix]] in the form | ||
| + | $$ | ||
| + | \mathop{\rm ch} V ( \Lambda ) = \ | ||
| − | + | \frac{\sum _ {w \in W } | |
| − | + | \mathop{\rm det} ( w ) e ^ {w ( \Lambda + \rho ) - \rho } }{\prod _ {\alpha \in \mathbf R ^ {+} } | |
| − | + | (1 - e ^ {- \alpha } ) } | |
| − | + | . | |
| + | $$ | ||
| − | (Recently, O. Mathieu and S. Kumar have removed the assumption of symmetrizability; see [[#References|[a5]]] for a detailed exposition.) Specializing | + | (Recently, O. Mathieu and S. Kumar have removed the assumption of symmetrizability; see [[#References|[a5]]] for a detailed exposition.) Specializing $ \Lambda = 0 $( |
| + | i.e. the trivial representation) yields a very nice proof of the Macdonald identity. A different proof of the Macdonald identity using $ \theta $- | ||
| + | functions has been given by E. Looyenga [[#References|[a3]]]. | ||
| − | The Rogers–Ramanujan identities and their higher analogues are of a more delicate nature, and are related to the decomposition of the irreducible highest weight module | + | The Rogers–Ramanujan identities and their higher analogues are of a more delicate nature, and are related to the decomposition of the irreducible highest weight module $ V ( \Lambda ) $ |
| + | when restricted to a suitable Heisenberg subalgebra, see J. Lepowsky [[#References|[a4]]]. | ||
For a generalization to Lie superalgebras see also [[#References|[a6]]]. | For a generalization to Lie superalgebras see also [[#References|[a6]]]. | ||
Revision as of 16:27, 31 March 2020
Weyl formula
A formula that expresses the character $ \mathop{\rm ch} V ( \Lambda ) $ of an irreducible finite-dimensional representation of a semi-simple Lie algebra $ \mathfrak g $ over an algebraically closed field of characteristic 0 (cf. Character of a finite-dimensional representation of a semi-simple Lie algebra) in terms of its highest weight $ \Lambda $:
$$ \mathop{\rm ch} V ( \Lambda ) = \ \frac{\sum _ {w \in W } ( \mathop{\rm det} w) e ^ {w ( \Lambda + \rho ) } }{\sum _ {w \in W } ( \mathop{\rm det} w) e ^ {w ( \rho ) } } = $$
$$ = \ \frac{\sum _ {w \in W } ( \mathop{\rm det} w) e ^ {w ( \Lambda + \rho ) - \rho } }{\prod _ {\alpha \in \mathbf R ^ {+} } (1 - e ^ {- \alpha } ) } $$
(here $ W $ is the Weyl group and $ \rho = ( \sum _ {\alpha \in \mathbf R ^ {+} } \alpha )/2 $ is half the sum of the positive roots of the Lie algebra $ \mathfrak g $). Consequences of the character formula are the formula for the dimension of the representation:
$$ \mathop{\rm dim} V ( \Lambda ) = \ \prod _ {\alpha \in \mathbf R ^ {+} } \frac{( \Lambda + \rho , \alpha ) }{( \rho , \alpha ) } , $$
a formula for the multiplicity of a weight, and also Steinberg's formula for the number $ m _ \Lambda $ of occurrences of the irreducible $ \mathfrak g $- module $ V ( \Lambda ) $ in $ V ( \Lambda ^ \prime ) \otimes V ( \Lambda ^ {\prime\prime} ) $:
$$ m _ \Lambda = \ \sum _ {s, t \in W } \mathop{\rm det} (st) P ( \Lambda + 2 \rho - s ( \Lambda ^ \prime + \rho ) - t ( \Lambda ^ {\prime\prime} + \rho )), $$
where $ P ( \mu ) $ is the number of distinct presentations of an element $ \mu $ as a sum of positive roots (see [1]).
The character formula can be generalized to the case of irreducible representations of graded Lie algebras defined by an indecomposable Cartan matrix (see also Lie algebra, graded). This generalization leads to the following combinatorial identities:
$$ e (t) = \ \sum _ {j \in \mathbf Z } (-1) ^ {j} t ^ {j (3j + 1)/2 } $$
(Euler's identity);
$$ \frac{e ^ {2} (t) }{e (t ^ {2} ) } = \ \sum _ {j \in \mathbf Z } (-1) ^ {j} t ^ {j ^ {2} } $$
(Gauss' identity);
$$ e ^ {3} (t) = \ \sum _ {j \geq 0 } (-1) ^ {j} (2j + 1) ^ {j (j + 1)/2 } $$
(Jacobi's identity); where
$$ e (t) = \ \prod _ {n \geq 1 } (1 - t ^ {n} ); $$
$$ \prod _ {j \geq 1 } (1 - t ^ {5j - 4 } ) ^ {-1} (1 - t ^ {5j - 1 } ) ^ {-1} = \sum _ {n \geq 0 } \frac{t ^ {n ^ {2} } }{(1 - t) \dots (1 - t ^ {n} ) } $$
(the Rogers–Ramanujan identity); and others (see [3], [4]).
An analogue of the character formula can also be obtained for irreducible representations of certain simple Lie superalgebras (cf. Superalgebra) [2].
References
| [1] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) |
| [2] | D.A. Leites, "Formulas for the characters of irreducible finite-dimensional representations of simple Lie superalgebras" Funct. Anal. and Appl. , 14 (1980) pp. 106–109 Funktsional. Anal. i Prilozhen. , 14 : 2 (1980) pp. 35–38 |
| [3] | V.G. Kac, "Infinite-dimensional algebras, Dedekind's 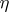 -function, classical Möbius function and the very strange formula" Adv. in Math. , 30 : 2 (1978) pp. 85–136 -function, classical Möbius function and the very strange formula" Adv. in Math. , 30 : 2 (1978) pp. 85–136 |
| [4] | J. Lepowsky, "Lie algebras and related topics" , Springer (1982) |
Comments
The denominator in the Weyl character formula can be written in two different ways: one as a sum, and the other as a product. This identity is called the Weyl denominator formula. It was I.G. Macdonald [a1] who proved that the denominator formula had a suitable generalization to the case of affine root systems. For the affine root system of type $ A _ {1} ^ {(1)} $, the formula of Macdonald comes down to the Jacobi triple product identity. Shortly afterwards it was V.G. Kac [a2] who realized that the Weyl character formula could be generalized to the case of so-called Kac–Moody algebras (cf. also Kac–Moody algebra) with a symmetrizable generalized Cartan matrix in the form
$$ \mathop{\rm ch} V ( \Lambda ) = \ \frac{\sum _ {w \in W } \mathop{\rm det} ( w ) e ^ {w ( \Lambda + \rho ) - \rho } }{\prod _ {\alpha \in \mathbf R ^ {+} } (1 - e ^ {- \alpha } ) } . $$
(Recently, O. Mathieu and S. Kumar have removed the assumption of symmetrizability; see [a5] for a detailed exposition.) Specializing $ \Lambda = 0 $( i.e. the trivial representation) yields a very nice proof of the Macdonald identity. A different proof of the Macdonald identity using $ \theta $- functions has been given by E. Looyenga [a3].
The Rogers–Ramanujan identities and their higher analogues are of a more delicate nature, and are related to the decomposition of the irreducible highest weight module $ V ( \Lambda ) $ when restricted to a suitable Heisenberg subalgebra, see J. Lepowsky [a4].
For a generalization to Lie superalgebras see also [a6].
References
| [a1] | I.G. Macdonald, "Affine root systems and Dedekind's eta function" Invent. Math. , 15 (1972) pp. 91–143 |
| [a2] | V.G. Kac, "Infinite-dimensional Lie algebras and Dedekind's eta function" Funct. Anal. and Appl. , 8 (1974) pp. 68–70 Funktsional. Anal. i Prilozhen. , 8 (1974) pp. 77–78 |
| [a3] | E. Looyenga, "Invariant theory for generalized root systems" Invent. Math. , 61 (1980) pp. 1–32 |
| [a4] | J. Lepowsky, "Affine Lie algebras and combinatorial identities" , Proc. 1981 Rutgers Lie Algebras Conference , Lect. notes in math. , 933 , Springer (1982) |
| [a5] | V.G. Kac, "Infinite-dimensional Lie algebras" , Birkhäuser (1983) |
| [a6] | V.G. Kac, "Representations of classical Lie superalgebras" , Lect. notes in math. , 676 , Springer (1978) pp. 597–626 |
Character formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Character_formula&oldid=44945