Difference between revisions of "Cramér-von Mises test"
(refs format) |
Ulf Rehmann (talk | contribs) m (tex done) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
| + | |||
{{MSC|62G10}} | {{MSC|62G10}} | ||
[[Category:Nonparametric inference]] | [[Category:Nonparametric inference]] | ||
| − | A [[Non-parametric test|non-parametric test]] for testing a hypothesis | + | A [[Non-parametric test|non-parametric test]] for testing a hypothesis $ H _{0} $ |
| + | which states that independent and identically-distributed random variables $ X _{1} \dots X _{n} $ | ||
| + | have a given continuous distribution function $ F (x) $. | ||
| + | The Cramér–von Mises test is based on a statistic of the type | ||
| + | |||
| + | $$ | ||
| + | \omega _ n^{2} [ \Psi (F (x))] \ = \ | ||
| + | \int\limits _ {- \infty} ^ {+ \infty} | ||
| + | \left [ \sqrt n (F _{n} (x) - | ||
| + | F (x)) \right ]^{2} \Psi (F (x)) \ dF (x), | ||
| + | $$ | ||
| + | |||
| + | where $ F _{n} (x) $ | ||
| + | is the [[Empirical distribution|empirical distribution]] function constructed from the sample $ X _{1} \dots X _{n} $ | ||
| + | and $ \Psi (t) $ | ||
| + | is a certain non-negative function defined on the interval $ [0,\ 1] $ | ||
| + | such that $ \Psi (t) $, | ||
| + | $ t \Psi (t) $ | ||
| + | and $ t^{2} \Psi (t) $ | ||
| + | are integrable on $ [0,\ 1] $. | ||
| + | Tests of this type, based on the "square metric" , were first considered by H. Cramér {{Cite|C}} and R. von Mises {{Cite|M}}. N.V. Smirnov proposed putting $ \Psi (t) \equiv 1 $, | ||
| + | and showed that in that case, if the hypothesis $ H _{0} $ | ||
| + | is valid and $ n \rightarrow \infty $, | ||
| + | the statistic $ \omega^{2} = \omega _ n^{2} $ | ||
| + | has in the limit an [[Chi-squared test| "omega-squared" distribution]], independent of the hypothetical distribution function $ F (x) $. | ||
| + | A statistical test for testing $ H _{0} $ | ||
| + | based on the statistic $ \omega _ n^{2} $, | ||
| + | is called an $ \omega^{2} $( | ||
| + | Cramér–von Mises–Smirnov) test, and the numerical value of $ \omega _ n^{2} $ | ||
| + | is found using the following representation: | ||
| − | + | $$ | |
| + | \omega _ n^{2} \ = \ | ||
| + | { | ||
| + | \frac{1}{12n} | ||
| + | } + | ||
| + | \sum _ {j = 1} ^ n | ||
| + | \left [ F (X _{(j)} ) - | ||
| − | + | \frac{2j - 1}{2n} | |
| − | + | \right ]^{2} $$ | |
| − | where | + | where $ X _{(1)} \leq \dots \leq X _{(n)} $ |
| + | is the variational series based on the sample $ X _{1} \dots X _{n} $. | ||
| + | According to the $ \omega^{2} $ | ||
| + | test with significance level $ \alpha $, | ||
| + | the hypothesis $ H _{0} $ | ||
| + | is rejected whenever $ \omega _ n^{2} \geq \omega _ \alpha^{2} $, | ||
| + | where $ \omega _ \alpha^{2} $ | ||
| + | is the upper $ \alpha $- | ||
| + | quantile of the distribution of $ \omega^{2} $, | ||
| + | i.e. $ {\mathsf P} \{ \omega^{2} < \omega _ \alpha^{2} \} = 1 - \alpha $. | ||
| + | T.W. Anderson and D.A. Darling proposed a similarly constructed test, based on the statistic $ \omega _ n^{2} [(1 - F (x))/F(x)] $( | ||
| + | see {{Cite|AD}}). | ||
====References==== | ====References==== | ||
| Line 27: | Line 75: | ||
====Comments==== | ====Comments==== | ||
| − | Usually, the choice | + | Usually, the choice $ \Psi (t) \equiv 1 $ |
| + | is simply called the Cramér–von Mises test in Western literature. However, Smirnov first proposed making this choice and rewrote the statistic in the distribution-free form above. The limit distribution of $ \omega _ n^{2} $ | ||
| + | is independent of $ F $ | ||
| + | whatever the choice of $ \Psi $. | ||
| + | (The term "square metric" refers to the expression $ [ \sqrt n (F _{n} (x) - F (x))]^{2} $, | ||
| + | not to some choice of $ \Psi $.) | ||
| + | Cramér actually considered the test with $ \Psi (F (x)) \ dF (x) $ | ||
| + | replaced by $ dx $, | ||
| + | while von Mises used $ \lambda (x) \ dx $. | ||
An alternative to {{Cite|C}} is {{Cite|C2}}. | An alternative to {{Cite|C}} is {{Cite|C2}}. | ||
Revision as of 10:47, 1 February 2020
2020 Mathematics Subject Classification: Primary: 62G10 [MSN][ZBL]
A non-parametric test for testing a hypothesis $ H _{0} $ which states that independent and identically-distributed random variables $ X _{1} \dots X _{n} $ have a given continuous distribution function $ F (x) $. The Cramér–von Mises test is based on a statistic of the type
$$ \omega _ n^{2} [ \Psi (F (x))] \ = \ \int\limits _ {- \infty} ^ {+ \infty} \left [ \sqrt n (F _{n} (x) - F (x)) \right ]^{2} \Psi (F (x)) \ dF (x), $$
where $ F _{n} (x) $ is the empirical distribution function constructed from the sample $ X _{1} \dots X _{n} $ and $ \Psi (t) $ is a certain non-negative function defined on the interval $ [0,\ 1] $ such that $ \Psi (t) $, $ t \Psi (t) $ and $ t^{2} \Psi (t) $ are integrable on $ [0,\ 1] $. Tests of this type, based on the "square metric" , were first considered by H. Cramér [C] and R. von Mises [M]. N.V. Smirnov proposed putting $ \Psi (t) \equiv 1 $, and showed that in that case, if the hypothesis $ H _{0} $ is valid and $ n \rightarrow \infty $, the statistic $ \omega^{2} = \omega _ n^{2} $ has in the limit an "omega-squared" distribution, independent of the hypothetical distribution function $ F (x) $. A statistical test for testing $ H _{0} $ based on the statistic $ \omega _ n^{2} $, is called an $ \omega^{2} $( Cramér–von Mises–Smirnov) test, and the numerical value of $ \omega _ n^{2} $ is found using the following representation:
$$ \omega _ n^{2} \ = \ { \frac{1}{12n} } + \sum _ {j = 1} ^ n \left [ F (X _{(j)} ) - \frac{2j - 1}{2n} \right ]^{2} $$
where $ X _{(1)} \leq \dots \leq X _{(n)} $ is the variational series based on the sample $ X _{1} \dots X _{n} $. According to the $ \omega^{2} $ test with significance level $ \alpha $, the hypothesis $ H _{0} $ is rejected whenever $ \omega _ n^{2} \geq \omega _ \alpha^{2} $, where $ \omega _ \alpha^{2} $ is the upper $ \alpha $- quantile of the distribution of $ \omega^{2} $, i.e. $ {\mathsf P} \{ \omega^{2} < \omega _ \alpha^{2} \} = 1 - \alpha $. T.W. Anderson and D.A. Darling proposed a similarly constructed test, based on the statistic $ \omega _ n^{2} [(1 - F (x))/F(x)] $( see [AD]).
References
| [C] | H. Cramér, "Sannolikhetskalkylen och nåcgra av dess användningar" , Stockholm (1926) |
| [M] | R. von Mises, "Mathematical theory of probability and statistics" (1964) (Translated from German) |
| [S] | N.V. Smirnov, "On the 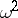 -distribution of von Mises" Mat. Sb. , 2 : 5 (1937) pp. 973–993 (In Russian) (French abstract) -distribution of von Mises" Mat. Sb. , 2 : 5 (1937) pp. 973–993 (In Russian) (French abstract)
|
| [BS] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
| [AD] | T.W. Anderson, D.A. Darling, "Asymptotic theory of certain "goodness-of-fit" criteria based on stochastic processes" Ann. of Math. Stat. , 23 (1952) pp. 193–212 |
Comments
Usually, the choice $ \Psi (t) \equiv 1 $ is simply called the Cramér–von Mises test in Western literature. However, Smirnov first proposed making this choice and rewrote the statistic in the distribution-free form above. The limit distribution of $ \omega _ n^{2} $ is independent of $ F $ whatever the choice of $ \Psi $. (The term "square metric" refers to the expression $ [ \sqrt n (F _{n} (x) - F (x))]^{2} $, not to some choice of $ \Psi $.) Cramér actually considered the test with $ \Psi (F (x)) \ dF (x) $ replaced by $ dx $, while von Mises used $ \lambda (x) \ dx $.
An alternative to [C] is [C2].
References
| [C2] | H. Cramér, "On the composition of elementary errors II" Skand. Aktuarietidskr. (1928) pp. 171–280 |
Cramér-von Mises test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cram%C3%A9r-von_Mises_test&oldid=44377