Difference between revisions of "Post class"
(Importing text file) |
m (→References: expand bibliodata) |
||
| Line 22: | Line 22: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.V. Yablonskii, G.P. Gavrilov, V.B. Kudryavtsev, "Functions of the algebra of logic and Post classes" , Moscow (1966) (In Russian)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> S.V. Yablonskii, G.P. Gavrilov, V.B. Kudryavtsev, "Functions of the algebra of logic and Post classes" , Moscow (1966) (In Russian) {{ZBL|0171.27701}}</TD></TR> | ||
| + | </table> | ||
Revision as of 18:22, 14 April 2018
A class of functions of the algebra of logic (Boolean functions, cf. Boolean function) that is closed with respect to the operation of superposition. E. Post has established that the set of such classes is enumerable and has given an explicit description of them. He has also shown that all of them are finitely generated, and he has constructed the lattice with respect to inclusion formed by these classes. The set of the above-mentioned classes is exhausted by the list 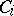 ,
, 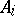 ,
, 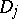 ,
, 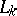 ,
, 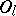 ,
, 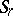 ,
, 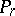 ,
, 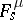 ,
, 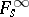 , where
, where 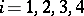 ;
; 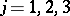 ;
; 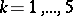 ;
; 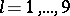 ;
; 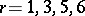 ;
; 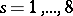 ;
; 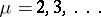 .
.
The class 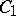 contains all functions of the algebra of logic;
contains all functions of the algebra of logic; 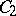 consists of all functions of the algebra of logic
consists of all functions of the algebra of logic 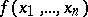 such that
such that 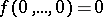 ;
; 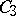 consists of all functions of the algebra of logic such that
consists of all functions of the algebra of logic such that 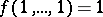 ;
; 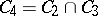 . The class
. The class 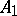 consists of all monotone functions of the algebra of logic (cf. Monotone Boolean function);
consists of all monotone functions of the algebra of logic (cf. Monotone Boolean function); 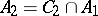 ;
; 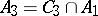 ;
; 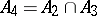 . The class
. The class 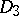 consists of all functions of the algebra of logic such that
consists of all functions of the algebra of logic such that  ;
; 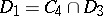 ;
; 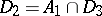 . The class
. The class 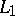 consists of all functions of the algebra of logic such that
consists of all functions of the algebra of logic such that 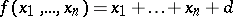
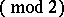 ,
, 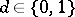 ;
; 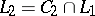 ;
; 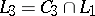 ;
; 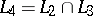 ;
; 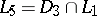 .
.
The class 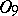 consists of all functions of the algebra of logic that are essentially dependent on not more than one variable;
consists of all functions of the algebra of logic that are essentially dependent on not more than one variable; 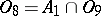 ;
; 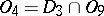 ;
; 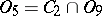 ;
; 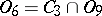 ;
; 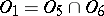 ;
; 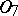 consists of all constant functions;
consists of all constant functions; 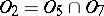 ;
; 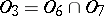 .
.
The class 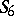 consists of all functions of the algebra of logic such that
consists of all functions of the algebra of logic such that 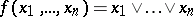 and all constant functions of the algebra of logic;
and all constant functions of the algebra of logic; 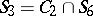 ;
; 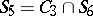 ;
; 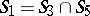 .
.
The class 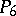 consists of all functions of the algebra of logic such that
consists of all functions of the algebra of logic such that 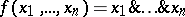 and all constant functions of the algebra of logic;
and all constant functions of the algebra of logic; 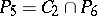 ;
; 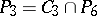 ;
; 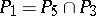 .
.
A function of the algebra of logic satisfies the condition 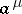 if
if 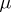 -tuples on which it is equal to
-tuples on which it is equal to  have a common coordinate equal to zero. In a similar way, by replacing
have a common coordinate equal to zero. In a similar way, by replacing  by
by 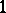 , one can introduce the condition
, one can introduce the condition 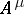 .
.
The class 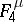 consists of all functions of the algebra of logic with the property
consists of all functions of the algebra of logic with the property 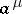 ;
; 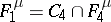 ;
; 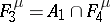 ;
; 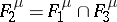 ;
; 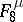 consists of all functions of the algebra of logic with the property
consists of all functions of the algebra of logic with the property 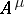 ;
; 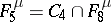 ;
; 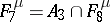 ;
; 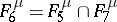 .
.
A function of the algebra of logic satisfies the condition 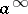 if all tuples on which it is equal to zero have a common coordinate equal to zero. Similarly, by replacing
if all tuples on which it is equal to zero have a common coordinate equal to zero. Similarly, by replacing  by
by 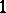 , one can introduce the property
, one can introduce the property 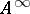 . The class
. The class 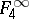 consists of all functions of the algebra of logic with the property
consists of all functions of the algebra of logic with the property 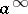 ;
; 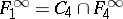 ;
; 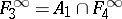 ;
; 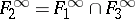 ;
; 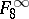 consists of all functions of the algebra of logic with the property
consists of all functions of the algebra of logic with the property 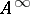 ;
; 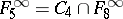 ;
; 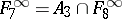 ;
; 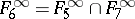 .
.
The lattice, with respect to inclusion, generated by these classes is shown in the figure. The classes are represented by points. Two points are connected by an arc if the underlying point represents a class immediately contained in the upper class (i.e. there are no intermediate classes between them).
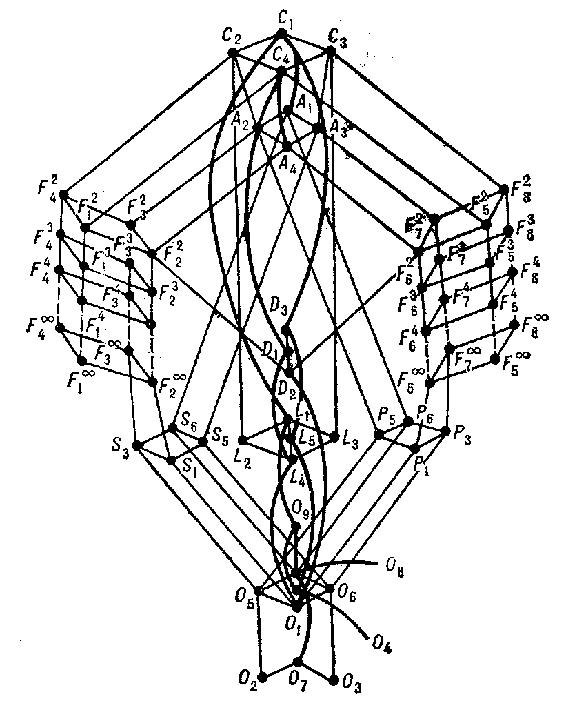
Figure: p074010a
References
| [1] | S.V. Yablonskii, G.P. Gavrilov, V.B. Kudryavtsev, "Functions of the algebra of logic and Post classes" , Moscow (1966) (In Russian) Zbl 0171.27701 |
Post class. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Post_class&oldid=43138