Difference between revisions of "Mapping cylinder"
From Encyclopedia of Mathematics
(Importing text file) |
(secondary title) |
||
| Line 1: | Line 1: | ||
| + | ''cylindrical construction'' | ||
| + | |||
A construction associating with every continuous mapping of topological spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m0622901.png" /> the topological space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m0622902.png" /> that is obtained from the topological sum (disjoint union) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m0622903.png" /> by the identification <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m0622904.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m0622905.png" />. The space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m0622906.png" /> is called the mapping cylinder of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m0622907.png" />, the subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m0622908.png" /> is a [[Deformation retract|deformation retract]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m0622909.png" />. The imbedding <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m06229010.png" /> has the property that the composite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m06229011.png" /> coincides with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m06229012.png" /> (here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m06229013.png" /> is the natural retraction of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m06229014.png" /> onto <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m06229015.png" />). The mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m06229016.png" /> is a homotopy equivalence, and from the homotopy point of view every continuous mapping can be regarded as an imbedding and even as a [[Cofibration|cofibration]]. A similar assertion holds for a [[Serre fibration|Serre fibration]]. For any continuous mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m06229017.png" /> the fibre and cofibre are defined up to a homotopy equivalence. | A construction associating with every continuous mapping of topological spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m0622901.png" /> the topological space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m0622902.png" /> that is obtained from the topological sum (disjoint union) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m0622903.png" /> by the identification <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m0622904.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m0622905.png" />. The space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m0622906.png" /> is called the mapping cylinder of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m0622907.png" />, the subspace <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m0622908.png" /> is a [[Deformation retract|deformation retract]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m0622909.png" />. The imbedding <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m06229010.png" /> has the property that the composite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m06229011.png" /> coincides with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m06229012.png" /> (here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m06229013.png" /> is the natural retraction of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m06229014.png" /> onto <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m06229015.png" />). The mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m06229016.png" /> is a homotopy equivalence, and from the homotopy point of view every continuous mapping can be regarded as an imbedding and even as a [[Cofibration|cofibration]]. A similar assertion holds for a [[Serre fibration|Serre fibration]]. For any continuous mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m062/m062290/m06229017.png" /> the fibre and cofibre are defined up to a homotopy equivalence. | ||
| Line 7: | Line 9: | ||
====Comments==== | ====Comments==== | ||
| − | The literal translation from the Russian yields the phrase | + | The literal translation from the Russian yields the phrase "cylindrical construction" for the mapping cylinder. This phrase sometimes turns up in translations. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G.W. Whitehead, "Elements of homotopy theory" , Springer (1978) pp. 22, 23</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G.W. Whitehead, "Elements of homotopy theory" , Springer (1978) pp. 22, 23</TD></TR></table> | ||
Revision as of 08:22, 10 April 2018
cylindrical construction
A construction associating with every continuous mapping of topological spaces 
the topological space 
that is obtained from the topological sum (disjoint union) 
by the identification 
, 
. The space 
is called the mapping cylinder of 
, the subspace 
is a deformation retract of 
. The imbedding 
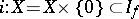has the property that the composite 
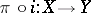coincides with 
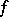(here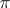 
is the natural retraction of 
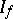onto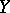 
). The mapping 
is a homotopy equivalence, and from the homotopy point of view every continuous mapping can be regarded as an imbedding and even as a cofibration. A similar assertion holds for a Serre fibration. For any continuous mapping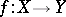 
the fibre and cofibre are defined up to a homotopy equivalence.
References
| [1] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) |
| [2] | R.E. Mosher, M.C. Tangora, "Cohomology operations and their application in homotopy theory" , Harper & Row (1968) |
Comments
The literal translation from the Russian yields the phrase "cylindrical construction" for the mapping cylinder. This phrase sometimes turns up in translations.
References
| [a1] | G.W. Whitehead, "Elements of homotopy theory" , Springer (1978) pp. 22, 23 |
How to Cite This Entry:
Mapping cylinder. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mapping_cylinder&oldid=43106
Mapping cylinder. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mapping_cylinder&oldid=43106
This article was adapted from an original article by A.F. Kharshiladze (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article