Difference between revisions of "Fisher z-distribution"
From Encyclopedia of Mathematics
m (Ivan moved page Fisher-z-distribution(2) to Fisher z-distribution: no need for (2)) |
m (link) |
||
| Line 11: | Line 11: | ||
The mathematical expectation and the variance are equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f0405006.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f0405007.png" />, respectively. | The mathematical expectation and the variance are equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f0405006.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f0405007.png" />, respectively. | ||
| − | If the random variable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f0405008.png" /> has the [[Fisher-F-distribution|Fisher <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f0405009.png" />-distribution]] with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050010.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050011.png" /> degrees of freedom, then the quantity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050012.png" /> has the Fisher <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050013.png" />-distribution with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050014.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050015.png" /> degrees of freedom. Along with the Fisher <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050016.png" />-distribution, known as the distribution of the [[Dispersion proportion|dispersion proportion]], the Fisher <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050017.png" />-distribution was originally introduced in the analysis of variance by R.A. Fisher (1924). His intention was that the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050018.png" />-distribution should be the basic distribution for testing statistical hypotheses in the analysis of variance. The Fisher <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050019.png" />-distribution was tabulated at the same time, and the first research was concerned with the statistic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050020.png" />, although in modern mathematical statistics one uses the simpler statistic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050021.png" />. | + | If the random variable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f0405008.png" /> has the [[Fisher-F-distribution|Fisher <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f0405009.png" />-distribution]] with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050010.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050011.png" /> degrees of freedom, then the quantity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050012.png" /> has the Fisher <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050013.png" />-distribution with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050014.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050015.png" /> degrees of freedom. Along with the Fisher <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050016.png" />-distribution, known as the distribution of the [[Dispersion proportion|dispersion proportion]], the Fisher <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050017.png" />-distribution was originally introduced in the [[analysis of variance]] by R.A. Fisher (1924). His intention was that the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050018.png" />-distribution should be the basic distribution for testing statistical hypotheses in the analysis of variance. The Fisher <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050019.png" />-distribution was tabulated at the same time, and the first research was concerned with the statistic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050020.png" />, although in modern mathematical statistics one uses the simpler statistic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f040/f040500/f04050021.png" />. |
====References==== | ====References==== | ||
Revision as of 20:15, 2 April 2018
A continuous probability distribution on the real line with density
 |
 |
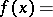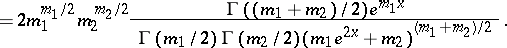The parameters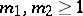 
are called the degrees of freedom. The characteristic function has the form
 |
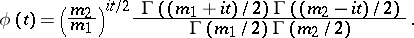The mathematical expectation and the variance are equal to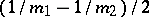 
and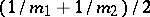 
, respectively.
If the random variable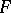 
has the Fisher 
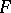-distribution with 
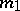and 
degrees of freedom, then the quantity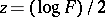 
has the Fisher 
-distribution with 
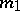and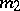 
degrees of freedom. Along with the Fisher 
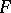-distribution, known as the distribution of the dispersion proportion, the Fisher 
-distribution was originally introduced in the analysis of variance by R.A. Fisher (1924). His intention was that the 
-distribution should be the basic distribution for testing statistical hypotheses in the analysis of variance. The Fisher 
-distribution was tabulated at the same time, and the first research was concerned with the statistic 
, although in modern mathematical statistics one uses the simpler statistic 
.
References
| [1] | R.A. Fisher, "On a distribution yielding the error functions of several well-known statistics" , Proc. Internat. Congress mathematicians (Toronto 1924) , 2 , Univ. Toronto Press (1928) pp. 805–813 |
Comments
The dispersion proportion is also called the variance ratio.
How to Cite This Entry:
Fisher z-distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fisher_z-distribution&oldid=43081
Fisher z-distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fisher_z-distribution&oldid=43081
This article was adapted from an original article by A.V. Prokhorov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article