Difference between revisions of "Goppa code"
(Category:Information and communication, circuits) |
(TeX partly done) |
||
| Line 1: | Line 1: | ||
| − | Let | + | Let $g(z)$ be a monic polynomial over the [[finite field]] $\mathbf{F}_{q^m}$ and let $L = \{\gamma_0,\ldots,\gamma_{n-1} \}$ be a set of $n$ elements of $\mathbf{F}_{q^m}$ such that $g(\gamma_i) \ne 0$ for $0 \le i < n$. The classical Goppa code $\Gamma(L,g)$ with Goppa polynomial $g(z)$ is the set of all words $(c_0,\ldots,c_{n-1})$ in $\mathbf{F}_q^n$ for which $\sum_{i=0}^{n-1} (z-\gamma_i)^{-1} c_i = 0 \pmod {g(z)}$. Here $(z-\gamma)^{-1}$ is to be interpreted as $-g(\gamma)^{-1} f(z)$ where $f(z)$ is the unique polynomial of degree ${}< \deg g(z)$ such that$(z-\gamma) f(z) \equiv 1 \pmod{g(z)}$. |
| − | The basic idea of this construction can be generalized as follows. Let | + | The basic idea of this construction can be generalized as follows. Let $X$ be a non-singular projective curve (in the sense of algebraic geometry) defined over the finite field $\mathbf{F}_q$. Let $\{P_1,\ldots,P_n\}$ be a set of rational points of $X$. Let $D$ be the [[$\mathbf{F}_{q^m}$|divisor]] $P_1+\cdots+ P_n$. Let $G$ be another divisor with support disjoint from $D$. Let $L(G)$ be the [[linear system]] associated to the divisor $G$, i.e. $L(G) = \{ f \in f(X)^* : D+(F) \ge 0 \}$, where $k(X)^*$ is the set of non-zero rational functions on $X$ and $(f)$ is the divisor of zeros and poles defined by $f \in k(X)^*$. The geometric Goppa code <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461036.png" /> of length <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461037.png" /> associated to the pair <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461038.png" /> is the image of the linear mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461039.png" /> defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461040.png" />. If the supports of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461041.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461042.png" /> are not disjoint, there is still a code associated to the pair <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461043.png" />, but not a canonical one; however, all the codes so obtained are equivalent in a suitable sense. A second code associated to the pair <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461044.png" /> is the following. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461045.png" /> be the vector space of rational differential forms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461046.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461047.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461048.png" />, with the zero form added. The second linear code <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461049.png" /> associated to the pair <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461050.png" /> is the image of the linear mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461051.png" /> defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461052.png" />. This is the construction which more directly generalizes the classical Goppa codes mentioned above. The codes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461053.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461054.png" /> are dual to each other. For fixed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461055.png" /> and varying <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461056.png" /> the codes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461057.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461058.png" /> yield the same family. |
At present (1989) one approach to finding good codes is to find curves with large numbers of rational points compared to their genus. This brings in advanced algebraic geometry. Using Shimura curves (modular curves) one now can find a sequence of codes which beats the Gilbert–Varshamov bound for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461059.png" />. For more details cf. [[#References|[a4]]], [[#References|[a7]]]–[[#References|[a9]]]. | At present (1989) one approach to finding good codes is to find curves with large numbers of rational points compared to their genus. This brings in advanced algebraic geometry. Using Shimura curves (modular curves) one now can find a sequence of codes which beats the Gilbert–Varshamov bound for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g044/g044610/g04461059.png" />. For more details cf. [[#References|[a4]]], [[#References|[a7]]]–[[#References|[a9]]]. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.H. van Lint, "Introduction to coding theory" , Springer (1982) {{MR|1540511}} {{ZBL|0485.94015}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Tietäväinen, "On the non-existence of perfect codes over finite fields" ''SIAM J. Appl. Math.'' , '''24''' (1973) pp. 88–96 {{MR|325260}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> R.J. McEliece, E.R. Rodemich, H. Rumsey, L.R. Welch, "New upper bounds on the rate of a code via the Delsarte–MacWilliams inequalities" ''IEEE Trans. Inform. Theory'' , '''23''' (1977) pp. 157–166 {{MR|439403}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> M.A. Tsfasman, S.G. Vladuts, T. Zink, "Modular curves, Shimura curves and Goppa codes, better than Varshamov–Gilbert bound" ''Math. Nachr.'' , '''109''' (1982) pp. 21–28 {{MR|0705893}} {{ZBL|0574.94013}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) (Updated reprint) {{MR|0893813}} {{ZBL|0611.10017}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> R. Hill, "A first course in coding theory" , Clarendon Press (1986) {{MR|0853914}} {{ZBL|0616.94006}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> J.H. van Lint, G. van der Geer, "Introduction to coding theory and algebraic geometry" , Birkhäuser (1988) {{MR|}} {{ZBL|0648.94011}} {{ZBL|0639.00048}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> V.D. Goppa, "Geometry and codes" , Kluwer (1988) {{MR|1029027}} {{ZBL|1097.14502}} </TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> M.A. Tsfasman, S.G. Vlăduts, "Algebraic geometric codes" , Kluwer (1989) {{MR|1003354}} {{ZBL|0674.94012}} </TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> J.H. van Lint, "Introduction to coding theory" , Springer (1982) {{MR|1540511}} {{ZBL|0485.94015}} </TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Tietäväinen, "On the non-existence of perfect codes over finite fields" ''SIAM J. Appl. Math.'' , '''24''' (1973) pp. 88–96 {{MR|325260}} {{ZBL|}} </TD></TR> | ||
| + | <TR><TD valign="top">[a3]</TD> <TD valign="top"> R.J. McEliece, E.R. Rodemich, H. Rumsey, L.R. Welch, "New upper bounds on the rate of a code via the Delsarte–MacWilliams inequalities" ''IEEE Trans. Inform. Theory'' , '''23''' (1977) pp. 157–166 {{MR|439403}} {{ZBL|}} </TD></TR> | ||
| + | <TR><TD valign="top">[a4]</TD> <TD valign="top"> M.A. Tsfasman, S.G. Vladuts, T. Zink, "Modular curves, Shimura curves and Goppa codes, better than Varshamov–Gilbert bound" ''Math. Nachr.'' , '''109''' (1982) pp. 21–28 {{MR|0705893}} {{ZBL|0574.94013}} </TD></TR> | ||
| + | <TR><TD valign="top">[a5]</TD> <TD valign="top"> P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) (Updated reprint) {{MR|0893813}} {{ZBL|0611.10017}} </TD></TR> | ||
| + | <TR><TD valign="top">[a6]</TD> <TD valign="top"> R. Hill, "A first course in coding theory" , Clarendon Press (1986) {{MR|0853914}} {{ZBL|0616.94006}} </TD></TR> | ||
| + | <TR><TD valign="top">[a7]</TD> <TD valign="top"> J.H. van Lint, G. van der Geer, "Introduction to coding theory and algebraic geometry" , Birkhäuser (1988) {{MR|}} {{ZBL|0648.94011}} {{ZBL|0639.00048}} </TD></TR> | ||
| + | <TR><TD valign="top">[a8]</TD> <TD valign="top"> V.D. Goppa, "Geometry and codes" , Kluwer (1988) {{MR|1029027}} {{ZBL|1097.14502}} </TD></TR> | ||
| + | <TR><TD valign="top">[a9]</TD> <TD valign="top"> M.A. Tsfasman, S.G. Vlăduts, "Algebraic geometric codes" , Kluwer (1989) {{MR|1003354}} {{ZBL|0674.94012}} </TD></TR> | ||
| + | </table> | ||
[[Category:Information and communication, circuits]] | [[Category:Information and communication, circuits]] | ||
| + | |||
| + | {{TEX|part}} | ||
Revision as of 19:22, 25 January 2018
Let $g(z)$ be a monic polynomial over the finite field $\mathbf{F}_{q^m}$ and let $L = \{\gamma_0,\ldots,\gamma_{n-1} \}$ be a set of $n$ elements of $\mathbf{F}_{q^m}$ such that $g(\gamma_i) \ne 0$ for $0 \le i < n$. The classical Goppa code $\Gamma(L,g)$ with Goppa polynomial $g(z)$ is the set of all words $(c_0,\ldots,c_{n-1})$ in $\mathbf{F}_q^n$ for which $\sum_{i=0}^{n-1} (z-\gamma_i)^{-1} c_i = 0 \pmod {g(z)}$. Here $(z-\gamma)^{-1}$ is to be interpreted as $-g(\gamma)^{-1} f(z)$ where $f(z)$ is the unique polynomial of degree ${}< \deg g(z)$ such that$(z-\gamma) f(z) \equiv 1 \pmod{g(z)}$.
The basic idea of this construction can be generalized as follows. Let $X$ be a non-singular projective curve (in the sense of algebraic geometry) defined over the finite field $\mathbf{F}_q$. Let $\{P_1,\ldots,P_n\}$ be a set of rational points of $X$. Let $D$ be the [[$\mathbf{F}_{q^m}$|divisor]] $P_1+\cdots+ P_n$. Let $G$ be another divisor with support disjoint from $D$. Let $L(G)$ be the linear system associated to the divisor $G$, i.e. $L(G) = \{ f \in f(X)^* : D+(F) \ge 0 \}$, where $k(X)^*$ is the set of non-zero rational functions on $X$ and $(f)$ is the divisor of zeros and poles defined by $f \in k(X)^*$. The geometric Goppa code 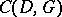 of length
of length  associated to the pair
associated to the pair 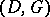 is the image of the linear mapping
is the image of the linear mapping 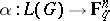 defined by
defined by 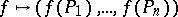 . If the supports of
. If the supports of 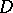 and
and  are not disjoint, there is still a code associated to the pair
are not disjoint, there is still a code associated to the pair 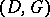 , but not a canonical one; however, all the codes so obtained are equivalent in a suitable sense. A second code associated to the pair
, but not a canonical one; however, all the codes so obtained are equivalent in a suitable sense. A second code associated to the pair 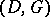 is the following. Let
is the following. Let 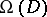 be the vector space of rational differential forms
be the vector space of rational differential forms 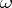 on
on 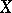 with
with 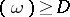 , with the zero form added. The second linear code
, with the zero form added. The second linear code 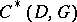 associated to the pair
associated to the pair 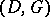 is the image of the linear mapping
is the image of the linear mapping 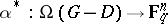 defined by
defined by 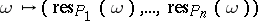 . This is the construction which more directly generalizes the classical Goppa codes mentioned above. The codes
. This is the construction which more directly generalizes the classical Goppa codes mentioned above. The codes 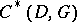 and
and 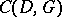 are dual to each other. For fixed
are dual to each other. For fixed 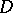 and varying
and varying 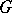 the codes
the codes 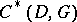 and
and 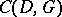 yield the same family.
yield the same family.
At present (1989) one approach to finding good codes is to find curves with large numbers of rational points compared to their genus. This brings in advanced algebraic geometry. Using Shimura curves (modular curves) one now can find a sequence of codes which beats the Gilbert–Varshamov bound for  . For more details cf. [a4], [a7]–[a9].
. For more details cf. [a4], [a7]–[a9].
References
| [a1] | J.H. van Lint, "Introduction to coding theory" , Springer (1982) MR1540511 Zbl 0485.94015 |
| [a2] | A. Tietäväinen, "On the non-existence of perfect codes over finite fields" SIAM J. Appl. Math. , 24 (1973) pp. 88–96 MR325260 |
| [a3] | R.J. McEliece, E.R. Rodemich, H. Rumsey, L.R. Welch, "New upper bounds on the rate of a code via the Delsarte–MacWilliams inequalities" IEEE Trans. Inform. Theory , 23 (1977) pp. 157–166 MR439403 |
| [a4] | M.A. Tsfasman, S.G. Vladuts, T. Zink, "Modular curves, Shimura curves and Goppa codes, better than Varshamov–Gilbert bound" Math. Nachr. , 109 (1982) pp. 21–28 MR0705893 Zbl 0574.94013 |
| [a5] | P.M. Gruber, C.G. Lekkerkerker, "Geometry of numbers" , North-Holland (1987) (Updated reprint) MR0893813 Zbl 0611.10017 |
| [a6] | R. Hill, "A first course in coding theory" , Clarendon Press (1986) MR0853914 Zbl 0616.94006 |
| [a7] | J.H. van Lint, G. van der Geer, "Introduction to coding theory and algebraic geometry" , Birkhäuser (1988) Zbl 0648.94011 Zbl 0639.00048 |
| [a8] | V.D. Goppa, "Geometry and codes" , Kluwer (1988) MR1029027 Zbl 1097.14502 |
| [a9] | M.A. Tsfasman, S.G. Vlăduts, "Algebraic geometric codes" , Kluwer (1989) MR1003354 Zbl 0674.94012 |
Goppa code. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Goppa_code&oldid=42787