Difference between revisions of "Hopf orders, applications of"
(link) |
(→References: expand bibliodata) |
||
| Line 16: | Line 16: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L. Childs, "Taming wild extensions with Hopf algebras" ''Trans. Amer. Math. Soc.'' , '''304''' (1987)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> C. Greither, "Extensions of finite group schemes, and Hopf Galois theory over a complete discrete valuation ring" ''Math. Z.'' , '''210''' (1992) pp. 37–67</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> T. Sekiguchi, N. Suwa, "Théories de Kummer–Artin–Schreier–Witt" ''C.R. Acad. Sci. Ser. I'' , '''319''' (1994) pp. 1–21</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> R.G. Underwood, "The group of Galois extensions in | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> L. Childs, "Taming wild extensions with Hopf algebras" ''Trans. Amer. Math. Soc.'' , '''304''' (1987) {{ZBL|0632.12013}}</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> C. Greither, "Extensions of finite group schemes, and Hopf Galois theory over a complete discrete valuation ring" ''Math. Z.'' , '''210''' (1992) pp. 37–67 {{ZBL|0737.11038}}</TD></TR> | ||
| + | <TR><TD valign="top">[a3]</TD> <TD valign="top"> T. Sekiguchi, N. Suwa, "Théories de Kummer–Artin–Schreier–Witt" ''C.R. Acad. Sci. Ser. I'' , '''319''' (1994) pp. 1–21 {{ZBL|0845.14023}}</TD></TR> | ||
| + | <TR><TD valign="top">[a4]</TD> <TD valign="top"> R.G. Underwood, "The group of Galois extensions in $KC_{p^2}$" ''Trans. Amer. Math. Soc.'' , '''349''' (1997) pp. 1503–1514 {{ZBL|0957.16010}}</TD></TR> | ||
| + | </table> | ||
Latest revision as of 19:17, 12 January 2018
Let  be a finite extension of the
be a finite extension of the 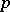 -adic rationals
-adic rationals 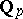 endowed with the
endowed with the 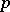 -adic valuation
-adic valuation  with
with 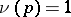 and let
and let 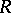 be its ring of integers (cf. also Extension of a field; Norm on a field;
be its ring of integers (cf. also Extension of a field; Norm on a field; 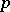 -adic number). Let
-adic number). Let  be the ramification index of
be the ramification index of 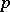 in
in 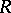 and assume that
and assume that 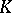 contains a primitive
contains a primitive 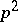 rd root of unity. If
rd root of unity. If 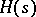 is an
is an 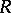 -Hopf order in
-Hopf order in 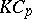 (cf. Hopf order), then the group scheme
(cf. Hopf order), then the group scheme 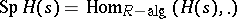 can be resolved, i.e., involved in a short exact sequence of group schemes
can be resolved, i.e., involved in a short exact sequence of group schemes 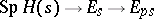 (taken in the flat topology). Here,
(taken in the flat topology). Here, 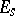 and
and 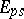 are represented by the
are represented by the 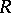 -Hopf algebras
-Hopf algebras 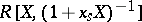 and
and 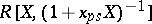 , respectively (
, respectively (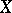 an indeterminate). One uses this short exact sequence in the long exact sequence in cohomology to construct
an indeterminate). One uses this short exact sequence in the long exact sequence in cohomology to construct 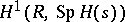 , which is identified with the group of
, which is identified with the group of 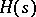 -Galois extensions of
-Galois extensions of 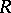 (cf. also Galois extension). One has
(cf. also Galois extension). One has 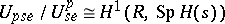 , where the class
, where the class 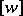 corresponds to the isomorphism class
corresponds to the isomorphism class 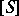 of the
of the 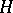 -Galois extension
-Galois extension
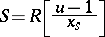 |
with  (see [a2]). Moreover, if
(see [a2]). Moreover, if 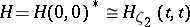 ,
, 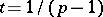 , is the dual of the Larson order
, is the dual of the Larson order 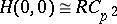 (cf. Hopf order), then
(cf. Hopf order), then 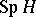 can be involved in the short exact sequence of group schemes
can be involved in the short exact sequence of group schemes 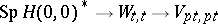 , where
, where 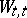 and
and 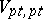 are represented by the
are represented by the 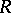 -Hopf algebras
-Hopf algebras 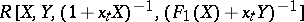 and
and 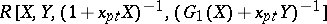 for appropriate polynomials
for appropriate polynomials 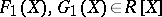 , respectively (see [a3]). Work has been completed to obtain a resolution of
, respectively (see [a3]). Work has been completed to obtain a resolution of  when
when 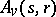 is an arbitrary
is an arbitrary 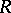 -Hopf order in
-Hopf order in  (see [a4]). This yields (via the long exact sequence in cohomology) a characterization of all
(see [a4]). This yields (via the long exact sequence in cohomology) a characterization of all 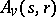 -Galois extensions. In general, if
-Galois extensions. In general, if 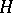 is an
is an 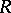 -Hopf order in
-Hopf order in 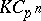 , then
, then 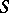 is an
is an 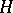 -Galois extension if and only if
-Galois extension if and only if 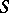 is an
is an 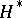 -Galois algebra (see [a1]).
-Galois algebra (see [a1]).
Examples of 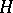 -Galois extensions where
-Galois extensions where 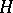 is a Tate–Oort–Larson order in
is a Tate–Oort–Larson order in 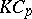 can be recovered using the corresponding classification theorem. For example, if
can be recovered using the corresponding classification theorem. For example, if 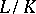 is a Kummer extension of prime degree, then
is a Kummer extension of prime degree, then 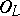 is an
is an 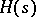 -Galois algebra if and only if the ramification number
-Galois algebra if and only if the ramification number 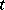 of
of 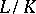 satisfies
satisfies 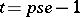 (see [a1]). Therefore,
(see [a1]). Therefore, 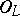 is an
is an 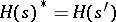 -Galois extension, thus
-Galois extension, thus
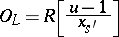 |
for some parameter  . Knowledge of Tate–Oort Galois extensions can also be used to characterize the ring of integers of certain degree-
. Knowledge of Tate–Oort Galois extensions can also be used to characterize the ring of integers of certain degree-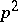 extensions. For example, if
extensions. For example, if 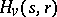 ,
, 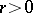 , is a Greither order with
, is a Greither order with 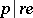 and
and 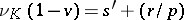 , then there exists a finite extension
, then there exists a finite extension 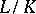 so that
so that 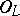 is an
is an 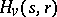 -Galois algebra. In this case,
-Galois algebra. In this case, 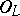 is of the form
is of the form
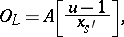 |
where  is an element in
is an element in 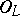 and
and 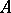 is an
is an 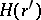 -Galois extension (see [a2]).
-Galois extension (see [a2]).
References
| [a1] | L. Childs, "Taming wild extensions with Hopf algebras" Trans. Amer. Math. Soc. , 304 (1987) Zbl 0632.12013 |
| [a2] | C. Greither, "Extensions of finite group schemes, and Hopf Galois theory over a complete discrete valuation ring" Math. Z. , 210 (1992) pp. 37–67 Zbl 0737.11038 |
| [a3] | T. Sekiguchi, N. Suwa, "Théories de Kummer–Artin–Schreier–Witt" C.R. Acad. Sci. Ser. I , 319 (1994) pp. 1–21 Zbl 0845.14023 |
| [a4] | R.G. Underwood, "The group of Galois extensions in $KC_{p^2}$" Trans. Amer. Math. Soc. , 349 (1997) pp. 1503–1514 Zbl 0957.16010 |
Hopf orders, applications of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hopf_orders,_applications_of&oldid=42724