Difference between revisions of "Variety in a category"
From Encyclopedia of Mathematics
(Importing text file) |
m (links) |
||
| Line 1: | Line 1: | ||
A notion generalizing that of a [[Variety of universal algebras|variety of universal algebras]]. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v0962801.png" /> be a [[Bicategory(2)|bicategory]] with products. A [[Full subcategory|full subcategory]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v0962802.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v0962803.png" /> is called a variety if it satisfies the following conditions: a) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v0962804.png" /> is an admissible monomorphism and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v0962805.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v0962806.png" />; b) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v0962807.png" /> is an admissible epimorphism and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v0962808.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v0962809.png" />; c) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628010.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628011.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628012.png" />. | A notion generalizing that of a [[Variety of universal algebras|variety of universal algebras]]. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v0962801.png" /> be a [[Bicategory(2)|bicategory]] with products. A [[Full subcategory|full subcategory]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v0962802.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v0962803.png" /> is called a variety if it satisfies the following conditions: a) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v0962804.png" /> is an admissible monomorphism and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v0962805.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v0962806.png" />; b) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v0962807.png" /> is an admissible epimorphism and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v0962808.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v0962809.png" />; c) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628010.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628011.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628012.png" />. | ||
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628013.png" /> is well-powered, that is, the admissible subobjects of any object form a set, then every variety is a [[ | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628013.png" /> is a [[well-powered category]], that is, the admissible subobjects of any object form a set, then every variety is a [[reflective subcategory]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628014.png" />. This means that the inclusion functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628015.png" /> has a left adjoint <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628016.png" />. The unit of this adjunction, the natural transformation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628017.png" />, has the property that for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628018.png" /> the morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628019.png" /> is an admissible epimorphism. In many important cases the functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628020.png" /> turns out to be right-exact, that is, it transforms the cokernel <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628021.png" /> of a pair of morphisms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628022.png" /> into the cokernel of the pair of morphisms <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628023.png" />, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628024.png" /> is a [[Kernel pair|kernel pair]] of the morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628025.png" />. Moreover, right exactness and the presence of the natural transformation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628026.png" /> are characteristic properties of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096280/v09628027.png" />. |
A variety inherits many properties of the ambient category. It has the structure of a bicategory, and is complete if the initial category is complete. | A variety inherits many properties of the ambient category. It has the structure of a bicategory, and is complete if the initial category is complete. | ||
| Line 13: | Line 13: | ||
====Comments==== | ====Comments==== | ||
| − | In a [[ | + | In a [[topos]], one also considers exponential varieties [[#References|[a1]]], which are full subcategories closed under arbitrary subobjects, products and power-objects. Such a subcategory is necessarily closed under quotients as well; it is a topos, and its inclusion functor has adjoints on both sides. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.J. Freyd, "All topoi are localic, or why permutation models prevail" ''J. Pure Appl. Alg.'' , '''46''' (1987) pp. 49–58</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.J. Freyd, "All topoi are localic, or why permutation models prevail" ''J. Pure Appl. Alg.'' , '''46''' (1987) pp. 49–58</TD></TR></table> | ||
Revision as of 17:50, 20 December 2017
A notion generalizing that of a variety of universal algebras. Let 
be a bicategory with products. A full subcategory 
of 
is called a variety if it satisfies the following conditions: a) if 
is an admissible monomorphism and 
, then 
; b) if 
is an admissible epimorphism and 
, then 
; c) if 
, 
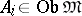, then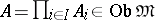 
.
If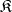 
is a well-powered category, that is, the admissible subobjects of any object form a set, then every variety is a reflective subcategory of 
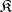. This means that the inclusion functor 
has a left adjoint 
. The unit of this adjunction, the natural transformation 
, has the property that for each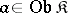 
the morphism 
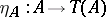is an admissible epimorphism. In many important cases the functor 
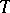turns out to be right-exact, that is, it transforms the cokernel 
of a pair of morphisms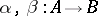 
into the cokernel of the pair of morphisms 
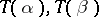, if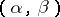 
is a kernel pair of the morphism 
. Moreover, right exactness and the presence of the natural transformation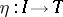 
are characteristic properties of 
.
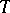A variety inherits many properties of the ambient category. It has the structure of a bicategory, and is complete if the initial category is complete.
In categories with normal co-images, as in the case of varieties of groups, it is possible to define a product of varieties. The structure of the resultant groupoid of varieties has been studied only in a number of special cases.
References
| [1] | M.Sh. Tsalenko, E.G. Shul'geifer, "Fundamentals of category theory" , Moscow (1974) (In Russian) |
| [2] | A. Fröhlich, "On groups over a d.g. near ring II. Categories and functors" Quart. J. Math. , 11 (1960) pp. 211–228 |
Comments
In a topos, one also considers exponential varieties [a1], which are full subcategories closed under arbitrary subobjects, products and power-objects. Such a subcategory is necessarily closed under quotients as well; it is a topos, and its inclusion functor has adjoints on both sides.
References
| [a1] | P.J. Freyd, "All topoi are localic, or why permutation models prevail" J. Pure Appl. Alg. , 46 (1987) pp. 49–58 |
How to Cite This Entry:
Variety in a category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Variety_in_a_category&oldid=42559
Variety in a category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Variety_in_a_category&oldid=42559
This article was adapted from an original article by M.Sh. Tsalenko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article