Difference between revisions of "Borcherds Lie algebra"
(Importing text file) |
m (link) |
||
| Line 1: | Line 1: | ||
''Borcherds algebra'' | ''Borcherds algebra'' | ||
| − | While a [[Kac–Moody algebra|Kac–Moody algebra]] is generated in a fairly simple way from copies of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b1302001.png" />, a Borcherds or generalized Kac–Moody algebra [[#References|[a1]]], [[#References|[a7]]], [[#References|[a9]]], [[#References|[a11]]] can also involve copies of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b1302002.png" />-dimensional Heisenberg algebra. Nevertheless, it inherits many of the Kac–Moody properties. Borcherds algebras played a key role in the proof of the Monstrous Moonshine conjectures [[#References|[a4]]], and also led to the development of a theory of automorphic products [[#References|[a5]]]. | + | While a [[Kac–Moody algebra|Kac–Moody algebra]] is generated in a fairly simple way from copies of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b1302001.png" />, a Borcherds or generalized Kac–Moody algebra [[#References|[a1]]], [[#References|[a7]]], [[#References|[a9]]], [[#References|[a11]]] can also involve copies of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b1302002.png" />-dimensional Heisenberg algebra. Nevertheless, it inherits many of the Kac–Moody properties. Borcherds algebras played a key role in the proof of the [[Moonshine conjectures|Monstrous Moonshine conjectures]] [[#References|[a4]]], and also led to the development of a theory of automorphic products [[#References|[a5]]]. |
First recall the definition of a Kac–Moody algebra. By a (symmetrizable) Cartan matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b1302003.png" /> one means an integral <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b1302004.png" />-matrix obeying | First recall the definition of a Kac–Moody algebra. By a (symmetrizable) Cartan matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b1302003.png" /> one means an integral <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b130/b130200/b1302004.png" />-matrix obeying | ||
Revision as of 22:04, 7 November 2017
Borcherds algebra
While a Kac–Moody algebra is generated in a fairly simple way from copies of 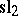 , a Borcherds or generalized Kac–Moody algebra [a1], [a7], [a9], [a11] can also involve copies of the
, a Borcherds or generalized Kac–Moody algebra [a1], [a7], [a9], [a11] can also involve copies of the  -dimensional Heisenberg algebra. Nevertheless, it inherits many of the Kac–Moody properties. Borcherds algebras played a key role in the proof of the Monstrous Moonshine conjectures [a4], and also led to the development of a theory of automorphic products [a5].
-dimensional Heisenberg algebra. Nevertheless, it inherits many of the Kac–Moody properties. Borcherds algebras played a key role in the proof of the Monstrous Moonshine conjectures [a4], and also led to the development of a theory of automorphic products [a5].
First recall the definition of a Kac–Moody algebra. By a (symmetrizable) Cartan matrix 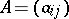 one means an integral
one means an integral  -matrix obeying
-matrix obeying
C1) 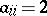 and
and 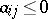 for all
for all 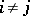 ; and
; and
C2) there is a diagonal matrix 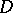 with each
with each 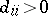 such that
such that 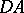 is symmetric. A (symmetrizable) Kac–Moody algebra
is symmetric. A (symmetrizable) Kac–Moody algebra 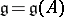 [a10], [a12] is the Lie algebra on
[a10], [a12] is the Lie algebra on 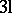 generators
generators 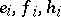 , obeying the relations:
, obeying the relations:
R1) 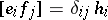 ,
, 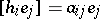 ,
, 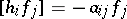 , and
, and 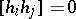 , for all
, for all 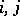 ; and
; and
R2) 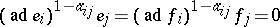 for all
for all 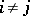 .
.
A Borcherds algebra is defined similarly. By a generalized Cartan matrix 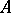 one means a (possibly infinite) matrix
one means a (possibly infinite) matrix 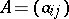 ,
, 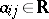 , obeying
, obeying
GC1) either 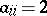 or
or 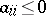 ;
;
GC2) 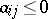 for
for 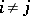 , and
, and 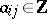 when
when 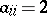 ; and
; and
GC3) there is a diagonal matrix 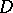 with each
with each 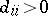 such that
such that 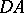 is symmetric. By the (symmetrizable) universal Borcherds algebra
is symmetric. By the (symmetrizable) universal Borcherds algebra 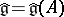 one means the Lie algebra (over
one means the Lie algebra (over 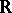 say) with generators
say) with generators 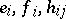 , subject to the relations [a3]:
, subject to the relations [a3]:
GR1) 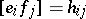 ,
, 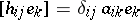 and
and 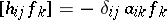 , for all
, for all 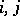 ;
;
GR2) 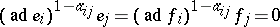 , whenever both
, whenever both 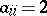 and
and 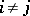 ; and
; and
GR3) 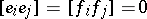 whenever
whenever 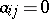 .
.
Note that for each 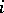 ,
, 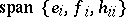 is isomorphic to
is isomorphic to 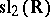 when
when 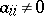 , and to the
, and to the  -dimensional Heisenberg algebra when
-dimensional Heisenberg algebra when 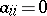 . Immediate consequences of the definition are that:
. Immediate consequences of the definition are that:
i) 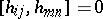 ;
;
ii) 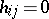 unless the
unless the 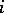 th and
th and 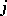 th column of
th column of 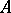 are identical;
are identical;
iii) the 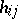 for
for 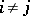 lie in the centre of
lie in the centre of 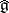 . Setting all
. Setting all 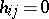 for
for 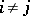 gives the definition of the (symmetrizable) Borcherds algebra
gives the definition of the (symmetrizable) Borcherds algebra 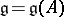 [a1]. This central extension
[a1]. This central extension 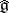 of
of 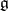 is introduced for its role in the characterization of Borcherds algebras below. If
is introduced for its role in the characterization of Borcherds algebras below. If 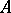 has no zero columns, then
has no zero columns, then 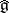 equals its own universal central extension [a3]. An important technical point is that both
equals its own universal central extension [a3]. An important technical point is that both 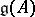 and
and 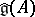 have trivial radical.
have trivial radical.
The basic structure theorem [a1] is that of Kac–Moody algebras. Let 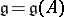 be a symmetrizable Borcherds algebra. Then:
be a symmetrizable Borcherds algebra. Then:
a) 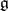 has triangular decomposition
has triangular decomposition 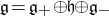 , where
, where 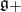 is the subalgebra generated by the
is the subalgebra generated by the 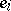 ,
, 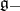 is generated by the
is generated by the 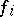 , and
, and  is the Cartan subalgebra. Also,
is the Cartan subalgebra. Also, 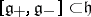 and
and 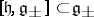 .
.
b) 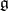 has a root space decomposition: formally calling
has a root space decomposition: formally calling 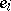
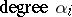 and
and 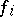
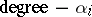 , and defining
, and defining 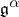 to be the subspace of degree
to be the subspace of degree 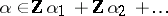 , one gets
, one gets 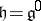 and
and 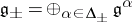 , where
, where 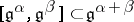 and
and 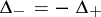 ;
;
c) there is an involution 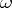 on
on 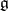 for which
for which 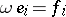 ,
, 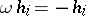 , and
, and 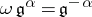 ;
;
d) 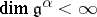 and
and 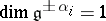 ;
;
e) there is an invariant symmetric bilinear form 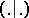 on
on 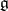 such that for each root
such that for each root 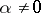 , the restriction of
, the restriction of 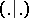 to
to 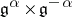 is non-degenerate, and
is non-degenerate, and 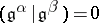 whenever
whenever 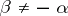 ;
;
f) there is a linear assignment 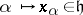 such that for all
such that for all 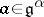 ,
, 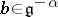 , one has
, one has 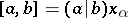 .
.
The condition that 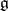 be symmetrizable (i.e. condition GC3)) is necessary for the existence of the bilinear form in e). For representation theory it is common to add derivations, so that the roots
be symmetrizable (i.e. condition GC3)) is necessary for the existence of the bilinear form in e). For representation theory it is common to add derivations, so that the roots 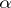 will lie in a dual space
will lie in a dual space 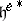 . In particular, define
. In particular, define  for any
for any 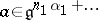 ; then each linear mapping
; then each linear mapping 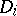 is a derivation, and adjoining these to
is a derivation, and adjoining these to 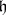 defines an Abelian algebra
defines an Abelian algebra 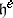 . The simple root
. The simple root 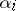 can be interpreted as the element of
can be interpreted as the element of 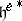 obeying
obeying 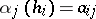 and
and 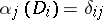 . Construct the induced bilinear form
. Construct the induced bilinear form 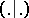 on
on 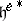 , obeying
, obeying  .
.
The properties a)–f) characterize Borcherds algebras. Let 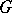 be a Lie algebra (over
be a Lie algebra (over 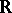 ) satisfying the following conditions:
) satisfying the following conditions:
1) 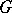 has a
has a 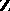 -grading
-grading 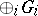 (cf. also Lie algebra, graded), and
(cf. also Lie algebra, graded), and 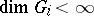 for all
for all 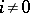 ;
;
2) 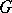 has an involution
has an involution 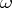 sending
sending 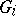 to
to 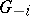 and acting as
and acting as 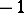 on
on 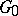 ;
;
3) 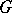 has an invariant bilinear form
has an invariant bilinear form 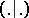 invariant under
invariant under 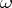 such that
such that 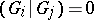 if
if 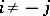 , and such that
, and such that 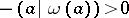 if
if 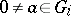 for
for 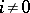 . Then there is a homomorphism
. Then there is a homomorphism 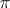 from some
from some 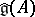 to
to 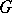 whose kernel is contained in the centre of
whose kernel is contained in the centre of 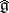 , and
, and 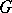 is the semi-direct product of the image of
is the semi-direct product of the image of 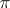 with a subalgebra of the Abelian subalgebra
with a subalgebra of the Abelian subalgebra 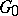 . That is,
. That is, 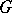 is obtained from
is obtained from 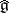 by modding out some of the centre and adding some commuting derivations. See e.g. [a4] for details.
by modding out some of the centre and adding some commuting derivations. See e.g. [a4] for details.
Define 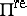 to be the set of all real simple roots, i.e. all
to be the set of all real simple roots, i.e. all 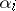 with
with 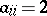 ; the remaining simple roots are the imaginary simple roots
; the remaining simple roots are the imaginary simple roots 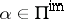 . The Weyl group (cf. also Weyl group)
. The Weyl group (cf. also Weyl group) 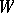 of
of 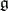 is the group generated by the reflections
is the group generated by the reflections 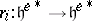 for each
for each  :
: 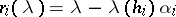 . It will be a (crystallographic) Coxeter group. The real roots of
. It will be a (crystallographic) Coxeter group. The real roots of 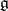 are defined to be those in
are defined to be those in 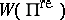 ; all other roots are called imaginary. For all real roots,
; all other roots are called imaginary. For all real roots, 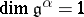 and
and 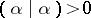 .
.
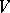 is called an integrable module if
is called an integrable module if
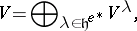 |
where the weight space 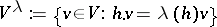 , with
, with 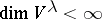 , and for each
, and for each 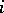 with
with 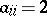 both
both 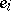 and
and 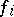 are locally nilpotent: i.e. for all
are locally nilpotent: i.e. for all 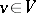 and all sufficiently large
and all sufficiently large 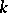 ,
, 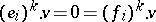 . By the character one means the formal sum
. By the character one means the formal sum
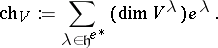 |
Let 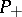 be the set of all weights
be the set of all weights 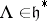 obeying
obeying 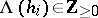 whenever
whenever 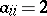 , and
, and 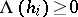 for all
for all 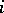 . Define the highest-weight
. Define the highest-weight 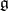 -module
-module  in the usual way as the quotient of the Verma module (cf. also Representation of a Lie algebra) by the unique proper graded submodule. Then one obtains the Weyl–Kac–Borcherds character formula: Choose
in the usual way as the quotient of the Verma module (cf. also Representation of a Lie algebra) by the unique proper graded submodule. Then one obtains the Weyl–Kac–Borcherds character formula: Choose 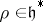 to satisfy
to satisfy
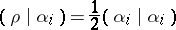 |
for all 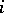 , and define
, and define 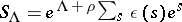 , where
, where  runs over all sums of
runs over all sums of 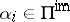 and
and 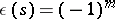 if
if  is the sum of
is the sum of 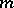 distinct mutually orthogonal imaginary simple roots, each of which is orthogonal to
distinct mutually orthogonal imaginary simple roots, each of which is orthogonal to 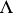 , otherwise
, otherwise 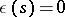 . Then
. Then
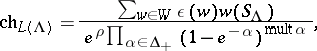 |
where 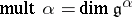 .
. 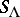 is the correction factor due to imaginary simple roots, much as the "extra" terms in the Macdonald identities are due to the imaginary affine roots. Putting
is the correction factor due to imaginary simple roots, much as the "extra" terms in the Macdonald identities are due to the imaginary affine roots. Putting 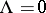 gives the denominator identity, as usual.
gives the denominator identity, as usual.
Thus, Borcherds algebras strongly resemble Kac–Moody algebras and constitute a natural and non-trivial generalization. The main differences are that they can be generated by copies of the Heisenberg algebra as well as 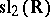 , and that there can be imaginary simple roots.
, and that there can be imaginary simple roots.
Interesting examples of Borcherds algebras are the Monster Lie algebra [a4], whose (twisted) denominator identity supplied the relations needed to complete the proof of the Monstrous Moonshine conjectures, and the fake Monster [a2]. A Borcherds algebra can be associated to any even Lorentzian lattice. The denominator identities of Borcherds algebras are often automorphic forms on the automorphism group 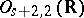 of the even self-dual lattice
of the even self-dual lattice 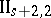 [a5]. They can serve as "automorphic corrections" to Lorentzian Kac–Moody algebras (see, for instance, [a6]). The space of BPS states in string theory carries a natural structure of a Borcherds-like algebra [a8].
[a5]. They can serve as "automorphic corrections" to Lorentzian Kac–Moody algebras (see, for instance, [a6]). The space of BPS states in string theory carries a natural structure of a Borcherds-like algebra [a8].
References
| [a1] | R.E. Borcherds, "Generalized Kac–Moody algebras" J. Algebra , 115 (1988) pp. 501–512 |
| [a2] | R.E. Borcherds, "The monster Lie algebra" Adv. Math. , 83 (1990) pp. 30–47 |
| [a3] | R.E. Borcherds, "Central extensions of generalized Kac–Moody algebras" J. Algebra , 140 (1991) pp. 330–335 |
| [a4] | R.E. Borcherds, "Monstrous moonshine and monstrous Lie superalgebras" Invent. Math. , 109 (1992) pp. 405–444 |
| [a5] | R.E. Borcherds, "Automorphic forms on 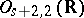 and infinite products" Invent. Math. , 120 (1995) pp. 161–213 and infinite products" Invent. Math. , 120 (1995) pp. 161–213 |
| [a6] | V.A. Gritsenko, V.V. Nikulin, "Siegel automorphic form corrections of some Lorentzian Kac–Moody Lie algebras" Amer. J. Math. , 119 (1997) pp. 181–224 |
| [a7] | K. Harada, M. Miyamoto, H. Yamada, "A generalization of Kac–Moody algebras" , Groups, Difference Sets, and the Monster , de Gruyter (1996) |
| [a8] | J.A. Harvey, G. Moore, "On the algebras of BPS states" Commun. Math. Phys. , 197 (1998) pp. 489–519 |
| [a9] | E. Jurisich, "An exposition of generalized Kac–Moody algebras" Contemp. Math. , 194 (1996) pp. 121–159 |
| [a10] | V.G. Kac, "Simple irreducible graded Lie algebras of finite growth" Math. USSR Izv. , 2 (1968) pp. 1271–1311 |
| [a11] | V.G. Kac, "Infinite dimensional Lie algebras" , Cambridge Univ. Press (1990) (Edition: Third) |
| [a12] | R.V. Moody, "A new class of Lie algebras" J. Algebra , 10 (1968) pp. 211–230 |
Borcherds Lie algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Borcherds_Lie_algebra&oldid=42263